| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Випишемо основні припущення, на яких заснована модель Солоу, і балансові співвідношення, які в ній виконуються.
В економіці існують два фактори виробництва, фізичний капітал До і праця L.
Це цікаво
Відповідаючи на закиди в недостатній реалістичності однопродуктовие і двохфакторну моделей, сам Р. Солоу помічав, що такі моделі як раз дозволяють виявити основні характеристики процесу економічного зростання, і з властивим йому дотепністю виправдовував свій вибір так: «Якби Бог вважав, що факторів виробництва більше, ніж два, Він навчив би нас без праці малювати тривимірні графіки »1.
Для простоти ми будемо вважати, що робоча сила збігається з усім населенням. Випуск єдиного продукту в економіці задається неокласичної виробничої функцією:

де функція F (K, L) задовольняє наступним трьом властивостям (див. також гл. 3):
для будь-яких До> 0 і L> 0, (До, L) > 0,FfcK, L)> О,F?K(До, L) < О, F [ 'L(До, L) <0.
тут Fv (K, L) = dF / ДК, гранична продуктивність капіталу, a F [(Kj) = dF / dL - гранична продуктивність праці. відповідно, Fj {K(K, L) = d2F / ДК2, F [ 'L(Ky L) = d2F / dL2. Ці властивості показують, що при додаванні одиниці фактора випуск зросте, але збільшення випуску буде тим менше, чим більше цього фактора вже є. Основні висновки моделі Солоу є наслідком саме зменшується граничної продуктивності капіталу;
3) умови і над2:
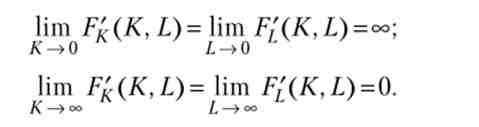
З цих трьох властивостей неокласичної виробничої функції випливає, що капітал і праця є суттєвими для виробництва факторами, в тому сенсі, що F (0, L) = F (K, 0) = 0.
Зауважимо також, що в силу позитивної однорідності справедливо рівність
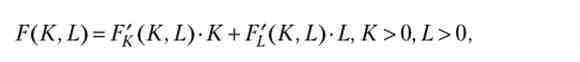
(Теорема Ейлера для однорідних функцій). Як говорилося в гл. 4 і 5, рівноваги на конкурентних ринках капіталу і праці означають, що граничні продукти факторів виробництва збігаються з їх ціною (реальною ставкою відсотка і реальною заробітною платою відповідно). Тоді вищенаведене рівність говорить про те, що весь випуск в економіці можна представити як суму доходу на капітал і загальної заробітної плати.
Як ми вже відзначали на початку глави, зростання прийнято визначати в величинах (випуску або споживання) на душу населення. Введемо поняття капиталовооруженности праці, т. Е. Величини капіталу на одного робітника (на душу населення), k-K / L і позначимо випуск на душу населення через y = Y / L. Неокласична виробнича функція може бути записана в інтенсивної формі:
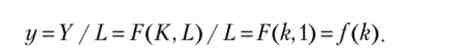
величину f (k) природно інтерпретувати як продуктивність праці в залежності від капиталовооруженности. Продуктивність визначається кількістю фізичної капіталу, до якого у одного робітника є «доступ». Тому формулювання моделі в величинах на душу населення зручна тим, що виключає залежність від масштабу: при постійній капиталовооруженности k збільшення або зменшення населення (робочої сили) не впливає на продуктивність.
Очевидно, що / (0) = 0, функція / (k) Монотонно зростає (fk) > 0) і строго ввігнута (F "(k) 0). Неважко перевірити, що граничні продукти факторів виробництва задаються рівностями
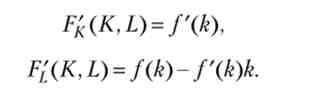
В якості стандартного прикладу неокласичної виробничої функції зручно уявляти собі функцію Кобба-Дугласа, F (K, L) = KaD ~a, яка в інтенсивній формі має вигляд f (k) = ka.
Все населення в моделі Солоу є однорідним, і споживачі (агенти) один від одного нічим не відрізняються. Тому населення можна вважати єдиним «репрезентативним» споживачем (сто ще можна інтерпретувати як суспільство в цілому). Цей «репрезентативний» споживач є власником як праці, так і капіталу. Таким чином, весь вироблений в періоді t продукт після виплати доходу на капітал і заробітної плати виявляється зосереджений у «репрезентативного» споживача. Він ділить випуск Yt на споживання Ct > 0 і заощадження, які в припущенні рівноваги на ринку капіталу збігаються з валовими інвестиціями It:

Зроблені інвестиції відразу ж перетворюються в новий капітал, тому запас основного капіталу в момент t +1 задається рівністю

де р - це коефіцієнт вибуття (норма амортизації) капіталу, що показує, яка частка запасу капіталу, наявного на поточний момент, не може бути використана в наступному періоді (через вихід з ладу, списання, і т. п.).
З приводу поведінки змінної L[M зазвичай припускають, що вона росте деяким постійним темпом (1 + /?):
