| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Перейдемо тепер до комплексного аналізу логіки поведінки економічного суб'єкта, який прагне постійно підтримувати оптимальну структуру свого майна, представленого портфелем цінних паперів. Для цього він на початку кожного періоду таким чином змінює структури свого портфеля, щоб максимізувати приріст його цінності до кінця періоду або, що те ж саме, забезпечити максимальну прибутковість майна, яка визначається як відношення доходу за період до цінності майна. Дохід портфеля складається з дивідендів і приросту цінності його активів, тому прибутковість визначається за формулою
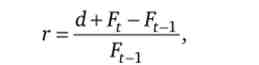
де г - прибутковість за період; d - відсоток (дивіденд), що виплачується за період; Fr Ft_x - ринковий курс портфеля відповідно в кінці і на початку періоду.
На рішення індивіда про розподіл загальної суми заощаджень між різними видами цінних паперів впливають чотири чинники: - прибутковість конкретного виду цінного паперу; - транзакційні витрати, пов'язані з перетворенням цінного паперу в гроші; - ступінь ризику отримання очікуваного доходу; - відношення індивіда до ризику.
Якби цінні папери відрізнялися тільки прибутковістю, то в портфелі економічного суб'єкта перебував би лише один вид цінного паперу, той, який має найбільшу норму прибутковості. Саме до такого висновку привів нас прознавств в попередньому розділі аналіз попиту на гроші як майно: поки дохід на облігацію перевищував очікувані втрати від зниження її курсу, в портфелі індивіда були тільки облігації; коли ці втрати стачо перевищувати суму процентних виплат, тоді майно індивіда складалося тільки з грошей. Однорідність портфеля обумовлена в даному випадку тим, що, крім прибутковості, ніякі інші властивості цінних паперів не бралися до уваги.
Коли при визначенні оптимальної структури портфеля враховуються також транзакційні витрати, як це було при дослідженні попиту на гроші для угод по моделі Баумоля - Тобіна, тоді в портфелі індивіда одночасно були і гроші, і облігації.
Розглянемо тепер роль ризику при формуванні портфеля цінних паперів. Ризик, пов'язаний з придбанням деяких видів цінних паперів, обумовлений тим, що очікуваний від них дохід - величина випадкова; він може приймати різні числові значення з певними ймовірностями.
Імовірність характеризує ступінь вірогідності настання деякої події. Імовірність гарантованого події приймають за одиницю, а неможливого - за нуль. Імовірність випадкової величини більше нуля, але менше одиниці, причому сума ймовірностей всіх можливих її значень дорівнює одиниці.
Існують два основних способи визначення ймовірності настання випадкової події: об'єктивний (історичний) і суб'єктивний (прогнозний). Об'єктивна оцінка ймовірності виводиться але даними статистичної обробки результатів спостережень за повторюваними процесами, що породжують випадкові події. Таким чином можна визначити ймовірність того, що в квітні поточного року в Москві середньомісячна температура буде вище нуля або що 31 грудня в місті не буде дорожньо-транспортних пригод. Іноді об'єктивну оцінку ймовірності настання деякої випадкової події можна дати апріорі: наприклад, ймовірність випадання цифри 3, як і будь-який інший від 1 до 6, при киданні шестигранного кубика дорівнює 1/6. Суб'єктивна оцінка ймовірності зводиться до більш-менш обгрунтованого прогнозу частоти появи можливих значень випадкової величини. В інвестиційних розрахунках зазвичай доводиться мати справу з новими технологіями, і тому з суб'єктивними оцінками ймовірності.
На основі заданих ймовірностей випадкових величин будують різні алгоритми визначення їх середніх очікуваних значень (математичні очікування). Найчастіше очікуване значення розраховують як середньозважену по можливостям величину. Так, якщо в наступному році прибуток фірми з ймовірністю 0,1 може дорівнювати і 15, і 30 ден. од., з імовірністю 0,2 - і 18, і 24 ден. од. і з імовірністю 0,4 - 20 ден. од., то очікувана величина складе: 0,1 (15 + 30) + 0,2 (18 + 24) + 0,4 - 20 = 20,9 ден. од.
Оскільки кількісні оцінки ймовірності не завжди достовірні, то фактичне значення прогнозованої величини може не збігтися з очікуваним. Звідси виникає поняття ризику: існує ризик, що фактична величина не співпаде з очікуваною. Імовірність відхилення фактичної величини від очікуваної тим більше, чим ширше розкид значень випадкової величини. Тому в якості міри ризику, притаманного рішенням з імовірнісним результатом, використовують так зване стандартне відхилення (ст) - середньоквадратичне абсолютне відхилення можливих значень випадкової змінної від очікуваного. У наведеному вище прикладі ризик не отримати в майбутньому році прибуток в розмірі 20,9 ден. од. складе
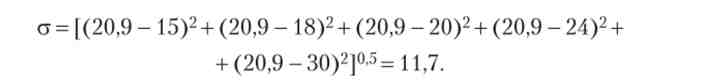
величину а2 називають дисперсією, або варіацією.
Дві випадкові змінні х, у можуть виявитися стохастично залежними або незалежними. Це залежить від того, наскільки поява значення х{ (I = 1, ..., п) пов'язане з появою значення у; (/ '= 1, ..., т). позначимо буквою W- ймовірність того, що змінна у прийме значення у;- тоді, коли змінна х прийме значення xi. Звідси характер залежності двох випадкових змінних можна відобразити наступною матрицею:
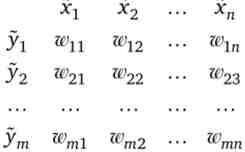
Кількісною мірою взаємозалежності двох випадкових змінних служить ковариация
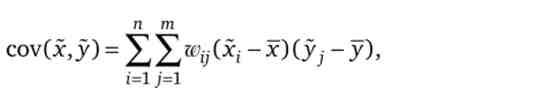
де х, у - математичні очікування відповідних величин.
Часто зручніше характеризувати ступінь взаємозалежності двох випадкових змінних за допомогою коефіцієнта кореляції: р = cov (Jc, у)/ схзу. За побудовою значення коефіцієнта кореляції знаходиться в інтервалі -1 < р < +1. Якщо cov (x, y) = 0 (відповідно р = 0), то х і у є стохастично незалежними або некорельованих випадковими змінними; при р = 1 випадкові значення х і у знаходяться в позитивній, а при р = -1 - в негативній лінійної залежності.
приклад 5.2
Випадкова змінна х з ймовірністю 0,3 може прийняти значення 50, з 0,2 - 100 і з 0,5 - 130. Випадкова змінна у з ймовірністю 0,6 прийме значення 150, з 0,4 - 275. Імовірність того, що х дорівнюватиме 50 тоді, коли у = 150, становить 0,2. Всі інші показники ймовірності спільного появи різних значень х і у представлені у вигляді такої матриці:
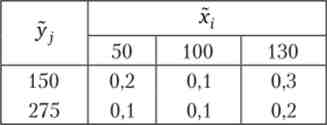
В даному прикладі математичні очікування
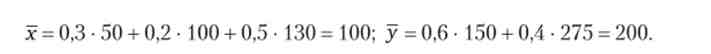
Визначимо стандартні відхилення
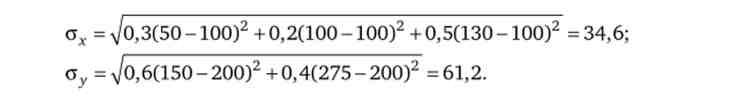
обчислимо ковариацию
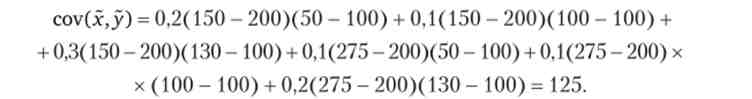
Тепер можна визначити коефіцієнт кореляції
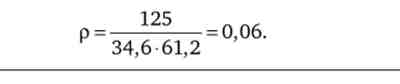
Надалі нам доведеться скористатися ще рядом положень теорії ймовірностей. Математичне сподівання суми випадкових змінних дорівнює сумі їх математичних очікувань:
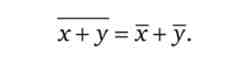
якщо а і b деякі константи, то

Дисперсія суми двох випадкових змінних відповідно
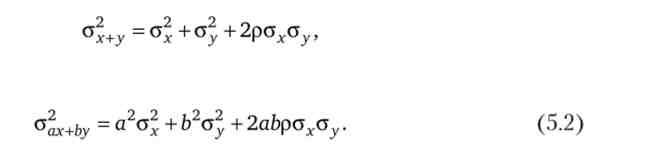
Якщо випадкові змінні стохастично незалежні, т. Е. Р = 0, тоді
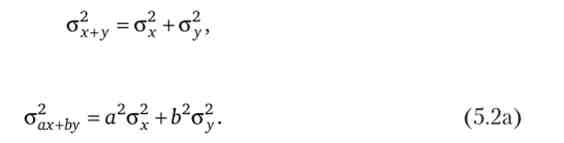
відповідно
Необхідність враховувати поряд з прибутковістю акції і її ризик значно розширює область вибору інвестора при формуванні портфеля. Припустимо, на фондовому ринку обертаються акції шести фірм. Характеристики цих акцій наведені в табл. 5.3.
Для більшої наочності наведемо ці дані в графічному вигляді (рис. 5.2).
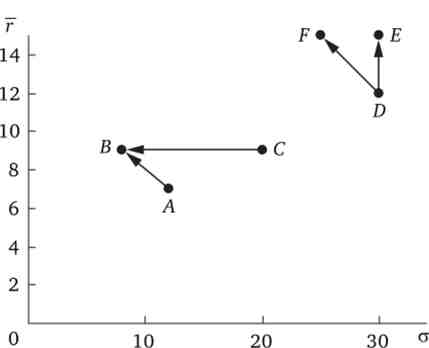
Таблиця 5.3. Прибутковість і ризик акцій
|
Показник,% |
Акції фірми |
|||||
|
Л |
В |
З |
D |
Е |
F |
|
|
г |
7 |
9 |
9 |
12 |
15 |
15 |
|
про |
12 |
8 |
20 |
30 |
30 |
25 |
Мал. 5.2. Прибутковість і ризик акцій 128
На перший погляд акції фірм А, С і D будуть витіснені з ринку, так як з точки зору типового інвестора по співвідношенню прибутковості і ризику акції фірми В переважніше акцій фірм Л і С, а замість акцій фірми D доцільніше купити акції або фірми?, або F. Насправді на фондовому ринку можуть одночасно і постійно звертатися акції всіх зазначених фірм. Чому це так, пояснює теорія портфеля.