Складання портфеля з двох різновидів акцій

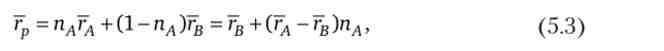
де г_р, г_А, г_в - очікувані прибутковості відповідно портфеля і акцій А і В; п_Ау (1 - п_А) = П_в - частки кожної з акцій в загальній цінності портфеля. Як розраховується частка кожного виду акцій в цінності портфеля, показано в табл. 5.4.

Таблиця 5.4. Частка акцій у цінності портфеля

Варіація прибутковості кожного з можливих варіантів портфеля відповідно до властивістю (5.2) дорівнює

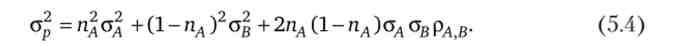
З рівняння (5.3) випливає, що при п_А + п_в = 1 прибутковість портфеля не може перевищувати прибутковість найбільш дохідної акції. Тому, здавалося б, складати змішаний портфель немає сенсу. Однак при р_{А в} 1 ризик портфеля менше середньозваженого ризику містяться в ньому акцій. Щоб переконатися в цьому, визначимо середньозважену стандартне відхилення двох акцій:

і зведемо обидві частини цієї рівності в квадрат:

Порівнюючи отриманий вираз з рівністю (5.4), легко помітити, що у всіх випадках, крім досконалої позитивної кореляції доходностей акцій, ризик портфеля менше середнього ризику входять в нього акцій.

Для визначення структури портфеля з мінімальним ризиком прирівняємо похідну функції (5.4) по п_А до нуля:

Щоб переконатися, що знайдений екстремум є мінімумом, визначимо другу похідну

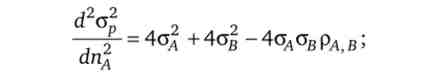
так як -1 < р_{4 в} < +1, то друга похідна завжди неотрицательна.

Рішення рівності (5.5) щодо п_л дає структуру портфеля з мінімальним ризиком

при р_{л в} = -1 частки кожного виду акцій, що мінімізують ризик, будуть

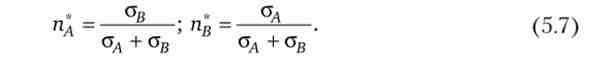
Портфель з такою структурою має нульовий ризик. У цьому можна переконатися, підставивши значення (5.7) в формулу (5.4) при р_{л в} = -1:

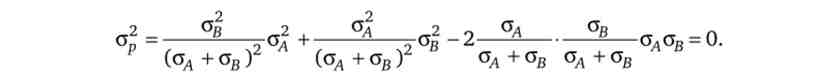
Портфель з двох стохастично незалежних акцій (р_{4 в} = 0) у відповідності до розділу (5.5) має мінімальний ризик при

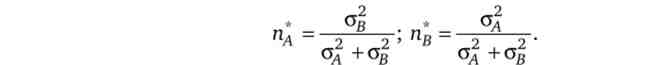
У такого портфеля

При досконалої позитивної кореляції двох акцій (р_{4 в} = +1) структура портфеля з мінімальним ризиком наступна:

він теж може бути безризиковим, так як

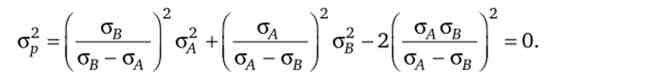
Але при цьому, як випливає з наведених формул, що визначають частки кожного виду акцій цього портфеля, одна з них повинна бути негативною: якщо з_в > G_{/ V} то п_в < 0, а якщо а_л > то п_А < 0. На практиці цьому відповідає продаж акцій «без покриття», т. Е. Реалізація акцій, взятих на час.

Однак не всі вибирають портфель з мінімальним ризиком. Деякі інвестори згодні мати більш ризиковий портфель з більш високою очікуваною прибутковістю. Тому потрібно знайти всі безліч можливих поєднань г_р, про_р- Щоб отримати функціональну залежність очікуваної прибутковості портфеля безпосередньо від ступеня його ризику: г_р = г_р(про_р), Потрібно вирішити рівняння (5.4) щодо п_л:

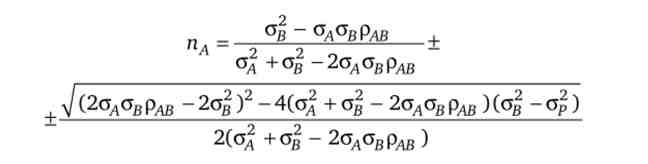
і це значення підставити у формулу (5.3).

На рис. 5.3 показано, як виглядають графіки функції Т_р(про_р) портфеля з двох акцій Аі В з очікуваними прибутковістю г_А= 2_уг_в = 18 і стандартними відхиленнями ст_л = 4, з_в = 6 при чотирьох різних коефіцієнтах кореляції.

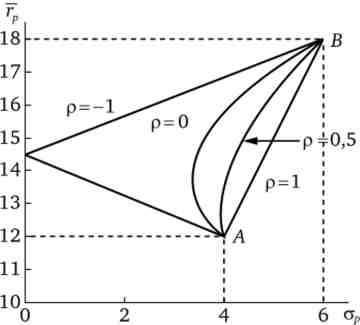
Мал. 5.3. Залежність прибутковості і ризику портфеля від коефіцієнта кореляції

У тих випадках, коли РЛ, В < 1, графік функції т ^ (а_р) Має точку перегину, що ділить область вибору інвестора на дві частини: верхню і нижню. Для інвестора, що бажає максимізувати прибутковість портфеля при заданій величині ризику, всі портфелі, представлені нижньою частиною кривої г_р(про_р), Неефективні тому, що кожному з них на верхній частині кривої відповідає портфель з таким же ризиком і більшою прибутковістю.

1. Теорія ефективної зарплати, поняття ефективної зарплати
   В індустріальних моделях передбачається сумлінну поведінку всіх працівників. У постіндустріальній економіці ускладнюються трудові функції, і у працівників з'являється можливість використовувати робочий час в своїх особистих цілях, т. Е. «Ухилятися» від роботи. Для боротьби з цим явищем рівень
2. Теоретичне обґрунтування зв'язку розвитку населення і кредиту
   Майже повсюдно нарощування кредитних комунікацій відбувалося під впливом зростання населення. Однак висхідний тренд кредиту періодично переривався і тимчасово відступав. Як тільки намічалося скорочення приросту і, тим більше, відбувалося падіння чисельності і щільності населення, кредитні
3. Технології і структура ринку
   Продукт виробляється декількома фірмами, причому фірма застосовує або стару технологію А, або нову технологію В. Зарплата працівника дорівнює одиниці. Власники фірми є також її працівниками, їх чисельність (L) незмінна, їх дохід (У) дорівнює сумі зарплати (I) і прибутку (л): технологія А.
4. Таблиці «галузь на галузь»
   Так само як для складання матриці «продукт на продукт» використовуються два методу, існують і два способи складання матриці «галузь на галузь»: 1) використання постійної структури продажів для продуктів, що передбачає залежність розподілу попиту між споживачами від продукту, а не від галузі
5. Сукупний попит і сукупна пропозиція
   В результаті вивчення матеріалу даного розділу студент повинен: знати обгрунтування використання рівняння кількісної теорії грошей як найпростішої моделі сукупного попиту; вплив макроекономічної політики держави на рух уздовж / зрушення кривої сукупного попиту; співвіднесення кривої сукупної
6. Сценарний метод
   . Кожен прогноз і кожне рішення, що стосуються майбутнього, неявно грунтуються на сценарії або ряді сценаріїв. Поняття «сценарій» спочатку означало тільки план або конспект п'єси. У прогнозуванні цим терміном позначають словесну картину якогось моменту майбутнього. сценарій - его упорядкована
7. Столітній механізм ціноутворення золота змінила електронна платформа
   20.03.2015 еталонні ціни на золото в злитках в Лондоні почали визначатися на електронному аукціоні ICE. Нова система прийшла на зміну історичному золотому фіксингу, який діяв з 1919 р 20.03.2015 на лондонській біржі ICE еталонна ціна золота в злитках, раніше відома як London Gold Fix, вперше
8. Стабілізаційна політика в закритій економіці
   №81 Умова рівноваги на ринку блага Умова рівноваги на грошовому ринку Функція сукупного попиту Умова рівноваги на ринку праці М Л = W D Функція сукупної пропозиції Рівноважний рівень цін Інші ендогенні параметри: у = 60 + 230/2 = 175; 175 = 45гУ- 2Л ' 2 -» N = 5; 11 '= 50; i = 0,05 175 + 16-