| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Чи достатньо знати очікувану прибутковість лотереї, щоб визначити вибір індивіда? Виявляється, що ні. Ілюстрацією цього служить так званий парадокс Бернуллі.
Історична довідка
Данило Бернуллі (1700-1782), швейцарський фізик і математик фламандського походження, творець математичної фізики. Представник знаменитої швейцарської родини Бернуллі, в якій протягом двох століть народжувалися видатні математики і натуралісти. Навчався в Базельському університеті на медичному факультеті. У 1725-1733 рр. працював на кафедрах фізіології і математики Санкт-Петербурзького університету. Потім повернувся в Базель, але залишився почесним членом Петербурзької академії наук. До кінця життя працював професором на кафедрі фізики Базельського університету. У 1748 р був обраний іноземним членом Паризької академії наук. Широко відомі його праці в області математичної фізики і теорії диференціальних рівнянь. Опублікував результати ряду досліджень з теорії ймовірності.
Припустимо, індивіду пропонується взяти участь в грі, пов'язаної з киданням монети. Якщо випадає «орел», то гравець отримує 2 руб. Якщо випадає «решка», монету продовжують кидати далі. Якщо «орел» випав на N-й спробі, то гравець отримує 2Л'Руб.
Знайдемо очікувану цінність (прибутковість) даної лотереї. Так як результати незалежні (передбачається чесна гра зі стандартними монетами), то ймовірність випадання «орла» на спробі N складе: р =
Тобто якщо «орел» випадає при першій спробі кидка монети, індивід
отримує 2 руб. з ймовірністю р, = -; якщо при другій спробі - 4 руб. 1 2
з ймовірністю Р2 - якщо при третій спробі - 8 руб. з ймовірністю
р3 = -; і т. д. Очікувана прибутковість буде дорівнює 8
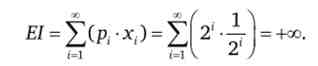
Однак, як зауважив Д. Бернуллі, зазвичай ніхто довго в цю гру не грає і не готовий багато платити за участь в ній. Чому так відбувається?
Роздуми на цю тему дозволили Бернуллі висунути концепцію очікуваної корисності невизначених результатів. Люди оцінюють лотереї не по очікуваної прибутковості, а на основі очікуваної корисності можливих доходів.
Функція очікуваної корисності показує математичне очікування корисності невизначених результатів:
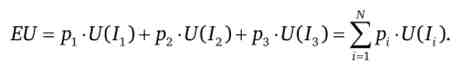
Існування функції очікуваної корисності виводиться на основі аксіом поведінки індивіда в умовах невизначеності і ризику. Якщо ці передумови виконуються, то функція очікуваної корисності існує, є єдиною, безперервної, зростаючої по доходу і лінійної по можливостям. Ця функція називається функцією корисності фон Неймана - Моргенштерна.
Історична довідка
Джон фон Нейман (1903-1957), американський математик угорського походження. Народився в Будапешті на території Австро-Угорської імперії. Вивчав математику в університеті Будапешта, хімічну інженерію в Цюріху.
З 1926 по 1930 р працював приват-доцентом в Берліні. З 1930 р був професором в Прінстонському університеті США. Зробив важливий внесок в квантову фізику, функціональний аналіз, теорію множин, інформатику та економіку. Є творцем теорії ігор і її застосування в економіці і соціальних науках.
Оскар Моргенштерн (1902-1978), американський економіст. Народився в Німеччині, закінчив Віденський університет. У 1929-1938 рр. викладав економічну теорію і статистику у Віденському університеті. У 1931-1938 рр. був директором Австрійського інституту по вивченню економічних циклів. З 1938 р керував програмою економетричних досліджень в Прінстонському університеті США. У 1976 р був обраний Почесним членом Американської економічної асоціації. Займався питаннями міжнародної торгівлі, розробив методологію статистичного і математичного аналізу економічних проблем. Застосував теорію ігор до дослідження ринкової економіки.
Нехай, наприклад, корисність грошового доходу для індивіда має вигляд: UU) = 77. Тоді очікувана корисність гри Бернуллі складе
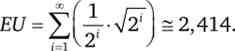
У цьому випадку ціна гри - сума грошей, яку готовий віддати індивід за участь в грі, буде дорівнює
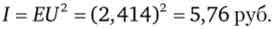
Парадокс Бернуллі вирішене!
На відміну від звичайної функції корисності, яка допускає будь-які позитивні монотонні трансформації, функція очікуваної корисності дозволяє лише такі перетворення, які зберігають порядок. До них відносяться аффінниє перетворення виду «множення на позитивну константу» і «додаток константи». Таким чином, якщо базова функція EUQ) характеризує переваги індивіда щодо ризикових ситуацій, то функція:? 1 / (7) = ос? 1 / (/) + р (а > 0) відображає ті ж переваги. Доказ цієї властивості базується на аксіомі незалежності простих і складних лотерей.
Важливою характеристикою ситуації невизначеності і ризику і вибору індивіда є передумова про наявність безризикового грошового еквівалента лотереї.
безризиковий еквівалент - це грошова сума, яку індивід може отримати, не беручи участь в лотереї, і яка еквівалентна очікуваної прибутковості лотереї. Для випадку двох випадків безризиковий еквівалент дорівнює
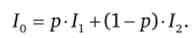
Наприклад, для ризикового проекту з імовірністю 0,25 отримання доходу в 100 тис. Руб. і ймовірністю 0,75 отримання доходу в 10 тис. руб. безризиковий грошовий еквівалент складе
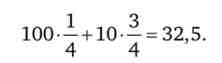
Завдання, що ілюструє концепцію
Функція корисності індивіда дорівнює: U = 120 - 200 / D (де U - сукупна корисність; D - дохід споживача). Споживачеві надається на вибір 4 тис. Руб. або лотерея, де він з ймовірністю 1/4 може виграти 10 тис. руб. або з ймовірністю 3/4 - 2 тис. руб. Що віддасть перевагу споживач: грати або отримати безризиковий еквівалент гри?
Рішення
Корисність безризикового еквівалента дорівнює
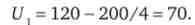Очікувана корисність лотереї дорівнює
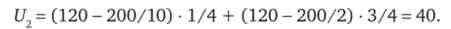
Так як t / j > U2, споживач вважатиме за краще не грати і отримати безризиковий еквівалент.