Області застосування схеми простих відсотків
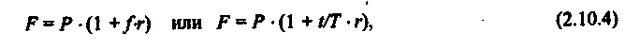
Де r - річна процентна ставка в частках одиниці;
t - тривалість фінансової операції в днях;
Т - кількість днів в році;
f - відносна довжина періоду до погашення позички.
Для наочності формулу (2.10.4) можна записати таким чином:
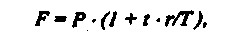
тобто дріб r / Т являє собою денну ставку, а твір t - r / T - ставку за t днів.
Визначаючи тривалість фінансової операції, прийнято день видачі та день погашення позики вважати за один день. Залежно від того, чому береться рівній тривалість року (кварталу, місяця), розмір проміжної процентної ставки може бути різним. Можливі два варіанти:
- точний відсоток, який визначається виходячи з точного числа днів у році (365 або 366), в кварталі (від 89 до 92), у місяці (від 28 до 31);
- звичайний відсоток, який визначається виходячи з наближеного числа днів у році, кварталі і місяці (відповідно 360, 90, 30).
При визначенні тривалості періоду, на який видана позичка, також можливі два варіанти:
- приймається в розрахунок точне число днів позики (розрахунок ведеться по днях);
- приймається в розрахунок приблизне число днів позики (виходячи з тривалості місяця в 30 днів).
Для спрощення процедури розрахунку точного числа днів користуються спеціальними таблицями (одна - для звичайного року, друга - для високосного), в яких всі дні в році послідовно пронумеровані. Тривалість фінансової операції визначається вирахуванням номера першого дня з номера останнього дня.
У тому випадку, коли в розрахунках використовується точний відсоток, береться і точна величина тривалості фінансової операції; при використанні звичайного відсотка може застосовуватися як точне, так і наближене число днів позики. Таким чином, розрахунок може виконуватися одним з трьох способів:
- звичайний відсоток з точним числом днів (застосовується в Бельгії, Франції);
- звичайний відсоток з наближеним числом днів (Німеччина, Данія, Швеція);
- точний відсоток з точним числом днів (Великобританія, США).
У практичному сенсі ефект від вибору того чи іншого способу залежить від значущості суми, що фігурує в процесі фінансової операції. Але й так ясно, що використання звичайних відсотків з точним числом днів позики, як правило, дає більший результат, ніж застосування звичайних відсотків з наближеним числом днів позики.
Приклад 2.16. Надано позика в розмірі 7 тис. руб. 10 лютого з погашенням 10 червня під 20% річних (рік невисокосний). Розрахувати різними способами суму до погашення (F).
Величина сплачують за користування позичкою відсотків залежить від кількості днів, яке береться в розрахунок. Точне число днів фінансової операції дорівнює 120. Наближене число днів позики одно: 18 дн. Лютий + 90 дн. (По 30 дн. Трьох місяців: березень, квітень, травень) + 10 дн. Червень=118 дн. Можливі варіанти повернення боргу:
1. У розрахунок приймаються точні відсотки і точне число днів позики:
F=7 - (1 + 120: 365 - 0,2)=7,460 тис. руб.
2. У розрахунок приймаються звичайні відсотки і точне число днів:
F=7 - (1 + 120: 360 - 0,2)=7,467 тис.
3. У розрахунок приймаються звичайні відсотки і наближене число днів:
F=7 - (1 + 118: 360 - 0,2)=7,459 тис. руб.
Інший вельми поширеною операцією короткострокового характеру, для оцінки якої використовуються розглянуті формули, є операція з обліку векселів банком. У цьому випадку користуються дисконтною ставкою. Одна з причин полягає в тому, що векселі можуть оформлятися по-різному, однак найчастіше банку доводиться мати справу з сумою до погашення, тобто з величиною FV. Схема дій у цьому випадку може бути наступною. Власник векселя на суму FV пред'являє його банку, який погоджується врахувати його, тобто купити, утримуючи на свою користь частину вексельної суми, яка нерідко також називається дисконтом. У цьому випадку банк пропонує власникові суму (PV), яке обчислюється виходячи з оголошеною банком ставки дисконтування (d). Очевидно, що чим вище значення дисконтної ставки, тим більшу суму утримує банк на свою користь. Розрахунок надається банком суми ведеться за формулою, що є наслідком формули (2.10.2):
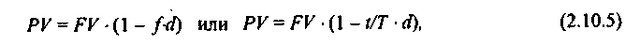
де f - відносна довжина періоду до погашення позики (відзначимо, що операція має сенс, коли число в дужках неотрицательно).
Приклад 2.17. Векселедержатель пред'явив для обліку вексель на суму 50 тис. руб. з терміном погашення 28.09.1997 р. Вексель пред'явлено 13.09.1997 р. Банк погодився врахувати вексель за обліковою ставкою 30% річних. Визначити суму, яку векселедержатель отримає від банку ..
Величина цієї суми розраховується за формулою (2.10.5) і становитиме:
PV=50 - (1 - 15: 360 - 0,3)=49,375 тис . руб.
Різниця між FV (номінальною величиною векселі) та PV (дисконтованою величиною векселя) являє собою комісійні, утримувані банком на свою користь за надану послугу. У даному прикладі вона склала 625 руб.
Можна виконати і більш глибокий факторний аналіз. Справа в тому, що дохід банку при обліку векселів складається з двох частин - відсотків за векселем, належних за час, що залишився до моменту погашення векселя, і власне комісійних за надану послугу. Як вже згадувалося вище, теоретична дисконтна ставка менше відсотковою. Однак на практиці, встановлюючи дисконтну ставку, банк, як правило, підвищує її залежно від умов, на яких видано вексель, ризику, пов'язаного з його погашенням, комісійних, які банк вважає за доцільне отримати за надану послугу, і т.п. Оскільки величина відсотків за векселем за період з моменту обліку до моменту погашення зумовлена, банк може варіювати лише розміром комісійних шляхом зміни облікової ставки. Перш ніж розглянути найпростіший приклад, викладемо логіку факторного аналізу доходу банку в цьому випадку.
Введемо наступні позначення:
PV - вартість векселя в момент його оформлення;
P1 - теоретична вартість векселя в момент обліку;
P2 - пропонована банком сума в обмін на вексель;
FV - вартість векселя до погашення;
? 0 - загальний дохід банку від операції.
З формул (2.10.4) і (2.10.5) видно, що функції PV=f (t) і FV=g (t) є лінійними щодо t, тобто процеси переходу PV> FV і FV> РV, а також структура факторного розкладання при обліку векселів можуть бути представлені графічно таким чином (рис. 2.6).
Логіка факторного розкладання доходу банку при обліку векселя
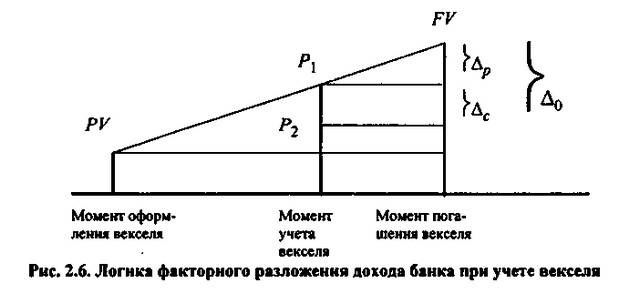
Швидкість нарощення вартості векселя, тобто крутизна нахилу прямої РVFV, залежить від рівня процентної ставки r, узгодженої між векселедавцем і векселедержателем. У міру наближення терміну погашення векселя його теоретична вартість постійно зростає на суму належних за минулий період відсотків, таким чином, в момент обліку векселя вона складе величину Р1, яку можна розрахувати за формулою (2.
Приклад 2.18. Підприємство продало товар на умовах споживчого кредиту з оформленням простого векселя: номінальна вартість 150 тис. руб., Термін векселя - 60 днів, ставка відсотка за наданий кредит - 15% річних. Через 45 днів з моменту оформлення векселя підприємство вирішило врахувати вексель у банку; запропонована банком дисконтна ставка становить: а) 20%, б) 25%. Розрахувати суми, одержувані підприємством і банком, якщо використовуються звичайні відсотки з точним числом днів.
Майбутня вартість векселя до моменту його погашення складе:
FV=150 - (l + 60: 360 - 0,15)=153,75 тис. руб.
Термінова вартість векселя в момент урахування його банком складе:
P1=150 - (1 + 45: 360 - 0,15)=152,813 тис. руб.
Пропонована банком сума розраховується за формулою (2.10.5):
а) P2=153,75 - (1 - 15: 360 - 0,2)=152,469 тис. руб.;
б) Р2=153,75 - (1 - 15: 360 - 0,25)=152,148 тис. руб.
Таким чином, банк отримує від операції відсотки за векселем за решту 15 днів у розмірі 937 руб. (153,75 - 152,81?), Величина яких не залежить від рівня дисконтної ставки, і комісійні за надану послугу в розмірі:
у випадку а): 344 руб. (152,813 - 152,469);
у разі 6): 665 руб. (152,813 - 152,148).
Дисконтування, здійснюване за формулою (2.10.5), називається банківським дисконтированием на відміну від математичного дисконтування, що є процесом, зворотним нарощенню первинного капіталу. При математичному дисконтуванні вирішується завдання знаходження такої величини капіталу Р, яка через п років при нарощенні по простих відсотках за ставкою r дорівнюватиме Rn. Вирішуючи (2.10.3) щодо Р, отримаємо:
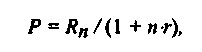
де п необов'язково ціле число років.
Приклад 2.19. Через півроку після укладення фінансової угоди про отримання кредиту боржник зобов'язаний заплатити 2,14 тис. руб. Яка початкова величина кредиту, якщо він виданий під 14% річних і нараховуються звичайні відсотки з наближеним числом днів?
Позначаючи Rn=2,14, п=180/360=0,5, r=0,14 і використовуючи математичне дисконтування, отримаємо:
P=2 , 14 / (1 + 0,5 - 0,14)=2 тис. руб.
Інформація, релевантна " Області застосування схеми простих відсотків "
- Поняття простого і складного відсотка
застосування простого відсотка доходи в міру їх нарахування доцільно знімати для споживання або використання в інших інвестиційних проектах або поточної діяльності . У практиці діяльності господарюючих суб'єктів часто зустрічаються фінансові контракти, що передбачають не поодинокі виплати на початку і в кінці терміну дії контракту, а ряди послідовних виплат. Найбільш наочним - 2.10.3. Процентні ставки і методи їх нарахування
схеми нарахування відсотків, ці розрахунки різноманітні зважаючи варіабельності умов фінансових контрактів щодо частоти і способів нарахування, а також варіантів надання та погашення - Гіпотези , теореми, теорії, концепції та моделі
схеми їх реалізації, то ці схеми називають моделями. При цьому не слід забувати, що як схеми біднішими життя, так і економічні моделі біднішими господарського життя, хоча і покликані її відображати. Зазвичай вони не можуть використовувати все багатство життя і тому використовують - Ефективна річна процентна ставка
схеми нарахування відсотків. Як правило, в цих контрактах обмовляється номінальна процентна ставка, зазвичай річна. Ця ставка, по-перше, не відображає реальної ефективності угоди і, по-друге, не може бути використана для зіставлень. Для того щоб забезпечити порівняльний аналіз ефективності таких контрактів, необхідно вибрати якийсь показник, який був би універсальним для будь - Складні відсотки
простий відсоток, який розраховується за формулою ДN=Д0 (1 + n - r '), де Д0-первісний внесок; r'-відсоткова ставка; ДN - вклади з урахуванням нарахованих відсотків за відповідні періоди; n-кількість років. Величина процентного доходу залежить не тільки від величини початкового строкового вкладу, але і від частоти нарахування відсотків на вклад. Розрахунки платежів за вкладом зазвичай проводяться на - 17.3.1. Загальні основи традиційного формування тарифних умов оплати праці
застосування нині тарифної системи зразка 1986 свідчить про її достатню універсальності і життєздатності та в умовах становлення ринкових відносин. Однак застосування цієї системи нині не означає її простого копірованія26. Суттєвим є те, що ця тарифна система повсюдно доповнена механізмом, який дає можливість переглядати такі визначальні її параметри, як - Питання 76. Статистика процентних ставок. Прості і складні відсотки Статистика процентних ставок є складовою частиною статистики фінансів. Базисним поняттям статистики процентних ставок є процентні гроші або відсотки.
прості відсотки: J1=P * i - за перший рік; J2=J1 + P * i=P * i * 2 - за другий рік; ... Jn=Jn-1 + P * i=P * i * n - за n років. У цьому випадку сума, яку зобов'язаний заплатити боржник з нарощеними за весь період відсотками, тобто нарощена сума боргу S, визначається за формулою простих відсотків: S=P * (1 + in). При терміні користування позичкою менше одного року: {foto227} - 4.12.4. Виробничо-фінансовий леверидж
схеми і зроблених пояснень стає зрозуміло, чому така велика увага з позиції стратегічного планування приділяється операційного та фінансового левериджу - саме умовно-постійні витрати виробничого та фінансового характеру значною мірою визначають кінцеві фінансові результати діяльності підприємства. Вибір більш-менш капіталомістких напрямків діяльності - Модель Кобба-Дугласа
проста, заснована тільки на двох виробничих факторах модель Кобба-Дугласа (названа по імені двох американських економістів). Вона виглядає таким чином: Q=AK? L? , (2.1) де Q - обсяг виробництва; К - розмір капіталу; L - витрати праці (у вартісному вираженні);? і? - Показники еластичності виробництва Q по відношенню відповідно до капіталу і праці (вони показують, на - 3. АНАЛІЗ КОРИСНОСТІ І ПОПИТУ
область застосування економічної теорії попиту, відмежовуючись від гедонізму Бентама - Джевонса. Тут відчувається відгук на критику маржиналистской теорії з боку психологів за те, що вона дотримується застарілої гедоністичної концепції людини, рухомого лише прагненням отримувати насолоди від задоволення своїх потреб. Маршалл погоджується з тим, що потрібно (і чим далі, тим - 3. Аналіз корисності і попиту
область застосування економічної теорії попиту, відмежовуючись від гедонізму Бентама - Джевонса. Тут відчувається відгук на критику мар-жіналістской теорії з боку психологів за те, що вона дотримується застарілої гедоністичної концепції людини, рухомого лише прагненням отримувати насолоди від задоволення своїх потреб. Маршалл погоджується з тим, що потреби (і чим далі, - Глава 4 КЛАСИЧНІ ФІГУРИ ТЕХНІЧНОГО АНАЛІЗУ
застосуванням набору типових фігур до цінового графіку, тобто той, який ми називаємо класичним, був створений одним з перших. Вже в Теорії Доу можна знайти типову схему руху індексу. І до цих пір набір фігур поповнюється новими, все більш і більш витонченими. За глибокої переконаності автора, прогнозування з використанням тільки класичних фігур не надто ефективно. По-перше, - Типи ощадних рахунків і відсотки
простий спосіб залучення грошових ресурсів - це ощадні рахунки. Ощадний рахунок - форма зберігання грошей у банку, при якій вкладник, отримуючи дохід у формі відсотка на вкладені грошові суми, може вилучити свої гроші. Існують два основних види ощадних рахунків: поточний і терміновий. Поточний ощадний рахунок припускає, що вкладник в будь-який зручний для нього момент може - 4.2. Інвестиційний криза та шляхи її подолання
застосування нового господарського механізму в цій сфері можуть з'явитися лише на наступному етапі реформ, за умови не тільки серйозного коригування практичних заходів закінчився етапу, а й уточнення самої концепції реформ інвестиційного - Реальна ставка відсотка коригує номінальну з урахуванням поправки на інфляцію.
відсотка коригує номінальну з урахуванням поправки на інфляцію. Іншими словами, її значення говорить вам про зміну в часі купівельної здатності ваших заощаджень. Реальна ставка відсотка дорівнює різниці номінальної процентної ставки і темпів інфляції: Реальна ставка відсотка=Номінальна ставка відсотка - Темпи інфляції. Наприклад, якщо банк встановлює номінальну ставку - Костромська область
області введено в усіх 303 муніципальних утвореннях. В основному по області ставки податку встановлені в розмірі 0,3% і 1,5%, тобто відповідають максимальним ставками, зазначеними у статті 394 НК - Питання для закріплення матеріалу
застосування імпортного тарифу країною з малої економікою. 4. У чому полягає відмінність оптимального тарифу і хто його вводить? У чому суть застосування імпортної квоти і які наслідки її застосування? Опишіть особливості застосування Део і його наслідки. 7. Назвіть інші методи обмеження імпорту. У чому економічний сенс експортного тарифу та експортної квоти? 9. Опишіть