Поняття простого і складного відсотка
- схема простих відсотків;
- схема складних відсотків.
Схема простих відсотків припускає незмінність бази, з якої відбувається нарахування. Нехай вихідний інвестується капітал дорівнює Р, необхідна прибутковість - r (в частках одиниці). Вважається, що інвестиція зроблена на умовах простого відсотка, якщо інвестований капітал щорічно збільшується на величину Р - r. Таким чином, розмір інвестованого капіталу (Rn) через n років буде дорівнює:
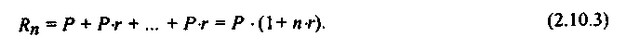
Вважається, що інвестиція зроблена на умовах складного відсотка, якщо черговий річний дохід обчислюється не з вихідної величини інвестованого капіталу, а з загальної суми , включає також і раніше нараховані і не затребувані інвестором відсотки. У цьому випадку відбувається капіталізація відсотків в міру їх нарахування, тобто база, з якої нараховуються відсотки, весь час зростає. Отже, розмір інвестованого капіталу дорівнюватиме:
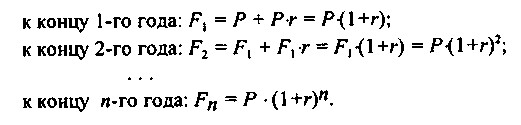
Як же співвідносяться величини Rn і Fn? Це надзвичайно важливо знати при проведенні фінансових операцій. Все залежить від величини п. Порівняємо множники нарощення за простим і складним відсоткам, тобто порівняємо (1 + п - r) і (1 + r) п. Очевидно, що при п=1 ці множники збігаються і дорівнюють (1 + r). Можна показати, що при будь-якому r справедливі нерівності (1 + n - r)> (1 + r) n, якщо 0
- Rn> Fn при 0
Графічно взаємозв'язок Fn і Rn можна представити таким чином (рис. 2.5):
Проста і складна схеми нарощення капіталу
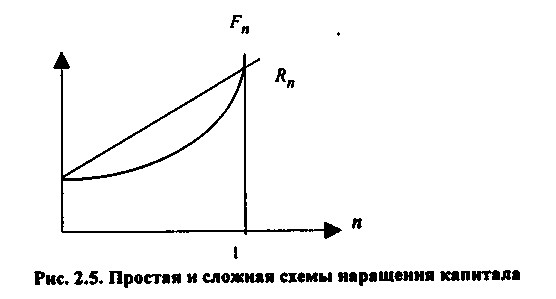
Таким чином , у разі щорічного нарахування відсотків для особи, що надає кредит:
- більш вигідною є схема простих відсотків, якщо термін позики менше одного року (відсотки нараховуються одноразово в кінці періоду);
- більш вигідною є схема складних відсотків, якщо термін позики перевищує один рік (відсотки нараховуються щорічно);
- обидві схеми дають однакові результати при тривалості періоду 1 рік і одноразовому нарахуванні відсотків.
У разі короткострокових позичок з терміном погашення до одного року в якості показника і береться величина, що характеризує питому вагу довжини підперіоди (дні, місяць, квартал, півріччя) у загальному періоді (рік). Довжина різних часових інтервалів в розрахунках може заокруглюватимуть: місяць - 30 днів; квартал - 90 днів; півріччя - 180 днів; рік - 360 (або 365, 366) днів.
Приклад 2.15. Розрахувати нарощену суму з вихідної суми в 1 тис. руб. при розміщенні її в банку на умовах нарахування простих і складних відсотків, якщо: а) річна ставка 20%, б) періоди нарощення: 90 днів, 180 днів, 1 рік, 5 років, 10 років. Думати, що в році 360 днів.
Результати розрахунків мають наступний вигляд:
(тис. крб.)

Таким чином, якщо кошти розміщені в банку на термін в 90 днів (менше одного року), то нарощена сума складе: при використанні схеми простих відсотків - 1,05 тис. руб.; при використанні схеми складних відсотків - 1,0466 тис. руб. Отже, більш вигідна перша схема (різниця - 3,4 руб.). Якщо термін розміщення грошових коштів перевищує один рік, ситуація змінюється діаметрально: вигідніша стає схема складних відсотків, причому нарощення в цьому випадку йде дуже швидкими темпами.
Використання в розрахунках складного відсотка у випадку багаторазового його нарахування більш логічно, оскільки в цьому випадку капітал, що генерує доходи, постійно зростає. При застосуванні простого відсотка доходи в міру їх нарахування доцільно знімати для споживання або використання в інших інвестиційних проектах або поточної діяльності.
У практиці діяльності господарюючих суб'єктів часто зустрічаються фінансові контракти, що передбачають не поодинокі виплати на початку і в кінці терміну дії контракту, а ряди послідовних виплат. Найбільш наочним прикладом такого грошового потоку є кредит, одержуваний одномоментно або поетапно із зобов'язанням погашати його протягом декількох послідовних періодів заздалегідь обумовленими частинами, рівними або нерівними. Розрахунки фінансових характеристик таких грошових потоків аналогічні розглянутим, з тією лише різницею, що кожна з виплат розглядається як окрема і незалежна від інших. Нарощена або дисконтована вартість кожної виплати визначається за вказаними вище формулами, а їх наведені до одного моменту вартості сумуються.
Формула складних відсотків є однією з базових формул у фінансових обчисленнях, тому для зручності розрахунків часто користуються спеціальними фінансовими таблицями, в яких табульовані значення мультиплицирующее множників виду (1 + r) n, 1 (1 + r) n і деяких інших.
Докладно про використання фінансових таблиць можна дізнатися в спеціальній літературі, наприклад, [Ковальов, Уланов, 1999].
Інформація, релевантна " Поняття простого і складного відсотка "
- Складні відсотки
простий відсоток, який розраховується за формулою ДN=Д0 (1 + n - r '), де Д0-первісний внесок ; r'-відсоткова ставка; ДN - вклади з урахуванням нарахованих відсотків за відповідні періоди; n-кількість років. Величина процентного доходу залежить не тільки від величини початкового строкового вкладу, але і від частоти нарахування відсотків на вклад. Розрахунки платежів за вкладом зазвичай проводяться на - Питання 76. Статистика процентних ставок. Прості і складні відсотки Статистика процентних ставок є складовою частиною статистики фінансів. Базисним поняттям статистики процентних ставок є процентні гроші або відсотки.
Прості відсотки: J1=P * i - за перший рік; J2=J1 + P * i=P * i * 2 - за другий рік; ... Jn=Jn-1 + P * i=P * i * n - за n років. У цьому випадку сума, яку зобов'язаний заплатити боржник з нарощеними за весь період відсотками, тобто нарощена сума боргу S, визначається за формулою простих відсотків: S=P * (1 + in). При терміні користування позичкою менше одного року: {foto227} - Терміни і поняття
складного відсотка Фактор дисконтування Грошові надходження (грошовий потік) Чиста приведена вартість Внутрішня норма прибутковості Рентабельність проекту Термін окупності - Редукція праці
поняття простої праці, в середині століття включалося початкову освіту, в кінці XX в. - Неповну середню освіту. В цілому висловити витрати праці в єдиній одиниці виміру, наприклад, в годинах робочого часу (трудоднях), не представляється можливим, з одного боку, через відсутність жорсткого критерію безпосередньої редукції праці, а з іншого - через неймовірно величезного обсягу робіт з - 3. Кругообіг товарів і послуг
простими, згрупувати і укрупнити, або, як висловлюються економісти, агрегувати, однорідні і подібні зв'язку. У агрегировании економічних відносин полягає одне із завдань макроекономіки. Для початку представимо найпростішу картину економічних зв'язків - укрупнену схему руху товарів і доходів, продукції та - Види послуг медичного закладу
просту, і комплексну медичну послугу. Детальна медична послуга - елементарна і неподільна послуга (ін'єкція, заклад історії хвороби тощо), яка не виступає об'єктом ціноутворення. Проста медична послуга - елементарна і неподільна: «Пацієнт» + «Спеціаліст»=«Один елемент профілактики, діагностики або лікування». Наприклад: операція, яку можна розкласти на - ПЕРІОДИЗАЦІЯ СТАНОВЛЕННЯ ТА РОЗВИТКУ СВІТОВОГО ГОСПОДАРСТВ
поняття «світове господарство». Етапи формування сучасної світової економіки. Підсистеми світового господарства. Система найважливіших показників. З часу свого формування в другій половині XIX століття світове господарство пройшло досить довгий шлях розвитку. Нині, через більш ніж століття, відбувається подальше зростання масштабів господарської діяльності окремих країн, диверсифікація їх - 5. Обчислення відсотка
просто комерційним звичаєм і зручним правилом обчислень. Вона не робить впливу на величину відсоткових ставок, визначених ринком. Діяльність підприємців сприяє встановленню єдиної ставки первинного відсотка у всій ринковій економіці. Якщо виявляється, що в будь-якому секторі ринку маржа між цінами на готівкові і майбутні товари відрізняється від маржі, існуючої в - 4. Рівні вартості
простого до складного, від аналізу до - Вартість грошей у часі. Складний відсоток і дисконтування
понятті, як вартість грошей у часі. Воно означає, що рубль, отриманий раніше, коштує більше, ніж рубль, отриманий пізніше. В економічному і фінансовому аналізі використовують спеціальну техніку для вимірювання поточної і майбутньої вартості однієї грошової міркою. Ця техніка (технічний прийом) називається дисконтуванням. Дисконтування є процесом, зворотним нарахуванню складного - Глава 6 СТРУКТУРА РИНКУ
поняття, що має безліч аспектів. Вона може визначатися характером об'єктів ринкових угод. Існують ринки факторів виробництва (земля, праця, капітал), ринки продуктів і послуг, ринки товарів тривалого (більше року) і нетривалого (до року) користування і т. - Модель Кобба-Дугласа
проста, заснована тільки на двох виробничих факторах модель Кобба-Дугласа (названа по імені двох американських економістів). Вона виглядає таким чином: Q=AK? L? , (2.1) де Q - обсяг виробництва; К - розмір капіталу; L - витрати праці (у вартісному вираженні);? і? - Показники еластичності виробництва Q по відношенню відповідно до капіталу і праці (вони показують, на - Основні терміни і поняття
відсоток, номінальний, реальний відсоток, Пофакторние розподіл доходів, персональний розподіл доходів, крива Лоренца, коефіцієнт Джинні, доцільний коефіцієнт, прожитковий мінімум, споживча - Типи ощадних рахунків і відсотки
простий спосіб залучення грошових ресурсів - це ощадні рахунки. Ощадний рахунок - форма зберігання грошей у банку, при якій вкладник, отримуючи дохід у формі відсотка на вкладені грошові суми, може вилучити свої гроші. Існують два основних види ощадних рахунків: поточний і терміновий. Поточний ощадний рахунок припускає, що вкладник в будь-який зручний для нього момент може - Стаття 4. Визначення основних понять
відсотків і більше ... Домінуючим визнається становище господарюючого суб'єкта, частка якого на ринку певного товару становить менше 65 відсотків, якщо це встановлено антимонопольним органом ... Не може бути визнано домінуючим становище господарюючого суб'єкта, частка якого на ринку певного товару не перевищує 35