Метод матриці взаємодій

Дозволяє планомірно досліджувати результати потенційної взаємодії елементів в прогнозованої сукупності подій. Він вимагає методичного опитування щодо потенційного впливу однієї події (якщо воно має відбутися) на інші події, що розглядається сукупності, причому бажано знати спосіб і сили зв'язку і час, в яке можна очікувати впливу однієї події на інше. Зібравши судження або дані, що зв'язують всі можливі комбінації подій за їх способу, силі і часу, можна провести аналіз, в ході якого переглядаються початкові оцінки ймовірності подій в їх сукупності.

Матриця взаємодій - метод, за допомогою якого здійснюється системний підхід до вивчення взаємозв'язків між прогнозами, що базується на взаємодії між прогнозованими подіями і їх «сумісністю». Матриця взаємодій вперше була використана при дослідженні методу Дельфі. Вона з'явилася як інструмент доопрацювання даного методу, так як передбачається, що експерти зосереджені кожен раз на якомусь одній події і не можуть прийняти до уваги взаємодії між прогнозованими подіями. Ідея обліку взаємозв'язків в ряду оцінок, отриманих від експертів, заснована на припущенні, що якщо такі взаємозв'язки існують, то вони повинні бути виявлені за допомогою процедури, що дозволяє перевірити «сумісність» цих оцінок і обгрунтувати перетворення початкових оцінок для отримання «сумісного» ряду. При цьому облік взаємозв'язків і взаємовпливів між прогнозованими подіями може служити додатковим джерелом інформації, що знижує рівень невизначеності.

Якщо позначити ряд подій, які повинні відбутися з різним ступенем ймовірності до певної дати через D_{, D₂, ..., D_n, а відповідні ймовірності їх звершення через Р [, Р2 - то події можна записати у вигляді матриці взаємодій (табл. 5.2).

Таблиця 5.2

матриця взаємодій

Примітка. Стрілки в клітинах матриці означають, що якщо, наприклад, станеться подія D₂, то ймовірність подій і D_A зросте.

Для проведення аналізу взаємовпливів необхідно мати наступну інформацію:

• безліч розглянутих подій А-,
• сукупність «безумовних» ймовірностей р, подій з безлічі А-,
• матриця взаємодій x_V}, елементи якої описують вплив здійснення події А_} на ймовірність події А_х
• модель взаємозв'язку між значеннями «безумовних» ймовірностей і параметрами взаємного впливу.

Існують різні моделі взаємозв'язку, форма яких вибирається з апріорних міркувань. Безліч досліджуваних явищ А_р вихідні значення «безумовних» ймовірностей р_{ і матриці взаємодій Хц зазвичай встановлюються за допомогою експертів. Так, наприклад, одна з апробованих моделей взаємозв'язку між р_} і х_1} мала такий вигляд:

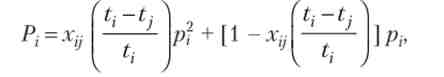
де Pj - корекція вихідної оцінки ймовірності події Л, при наступив подію Aj (- t:) / tj - відносне запізнювання події А- по відношенню до події А_х.

знаючи значення р_х, можна обчислити скориговане значення ймовірності р_х за законом повної ймовірності:

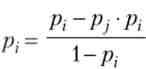
Процедура корекції ймовірностей може бути виконана за допомогою пакетів прикладних програм (Statistica, SPSS).

Наведемо приклад використання процедури матриці взаємодії для прогнозування можливостей використання в 2015 р електромобіля. У матрицю взаємодій були включені можливі події, оцінки ймовірності скоєння яких дані експертами (табл. 5.3).

Таблиця 53

Взаємопов'язані події і ймовірності їх звершення

Використовуючи теореми теорії ймовірностей, можна розрахувати оцінки матриці, що враховує ймовірності того, що зазначені події не відбудуться.

Потім дані з цих матриць обробляються за допомогою статистичних пакетів.

Ця процедура може проводитися в такій послідовності:

• 1) з набору подій проводиться випадковий вибір однієї події (наприклад, події 3);
• 2) за допомогою датчика випадкових чисел вибирається число від 0 до 1, яке порівнюється з первісною оцінкою ймовірності цієї події;
• 3) змінюються ймовірності інших подій в матриці з урахуванням того, що подія 3 не відбудеться;
• 4) випадковим чином вибирається з переліку подій (виключаючи подія 3) наступні подія, наприклад 6;
• 5) повторюється крок 2, і приймається рішення станеться подія 6 чи ні;
• 6) в залежності від того, відбудеться або не відбудеться подія 6, використовується відповідна матриця взаємодії для зміни ймовірностей інших подій переліку;
• 7) ця процедура повторюється для всіх подій; ймовірності появ подій, встановлені по її закінченні, є оцінками того, «відбудеться» або «не відбудеться» кожне з подій переліку, в результаті виходить так званий одиничний сценарій;
• 8) потім цей процес повторюється (зазвичай 100 раз); в результаті виробляється велика кількість сценаріїв, на основі яких для кожної події розраховуються «остаточні» оцінки ймовірностей, що відрізняються від початкових тим, що була врахована взаємозв'язок між оцінюваними подіями;
• 9) початкові і остаточні оцінки ймовірностей подій повинні бути близькі, якщо матриця «збалансована», т. Е. Якщо їх доречність чи не суперечить різними статистичними обмеженням.

Після виконання цієї процедури можна провести перевірку будь-якого з первинних пропозицій. Припустимо, прийнято рішення, що в 2015 р буде випущено 8 млн електромобілів. Іншими словами, приймається, що ймовірність першої події прагне до 1, т. Е. Ця подія безумовно трапиться. Виходячи з цього, повторюють процедуру обробки інформації за допомогою статистичних програм. Різниця між спочатку встановленими оцінками ймовірності і новими скоригованими оцінками, отриманими при вторинній обробці інформації, є результатом обліку зв'язків між подією, яке прийнято як достовірне, і іншими подіями даного переліку. Для даного прикладу в табл. 5.4 наведені початкові і скориговані оцінки ймовірностей подій.

Оцінка ймовірності подій

Таблиця 5.4

Метод взаємодій дозволяє уточнити оцінки ймовірностей звершення прогнозних подій будь-якого типу: технічних, екологічних, соціальних - з урахуванням зв'язку між ними. Разом з тим метод містить деякі довільні припущення щодо моделі корекції оцінок і елементи обчислювальної процедури. Принципова проблема при застосуванні даного методу - використання суб'єктивних ймовірностей і суб'єктивних оцінок впливу. Безперервне множення суб'єктивних оцінок призводить до складання сценарію з великими відхиленнями ймовірностей і подій. Інша проблема - це властиві методу спотворення, пов'язані з тим, що аналіз починають з цього взаємозв'язку. Це зумовлює явище майбутніх причинно-наслідкових зв'язків на основі сучасного способу мислення.

В останні роки розроблено ряд модифікацій методів взаємодії, в яких зроблені спроби подолати концептуальні суперечності, що виникають при його використанні.

Будь-яка комбінація подій, що відбулися відповідає деякому сценарієм Е_до, т. е. довільній сукупності подій з даного переліку. Це означає, що при розгляді системи з п подій теорітіче- скі можливими є г = 2^п комбінацій або сценаріїв. Наприклад, якщо до заданого моменту часу здійснилися події е_{, е₂, е₄,..., е_п, а подія е₃ не відбулося, то це відповідає одному з 2 "сценаріїв. Сума ймовірностей всіх сценаріїв дорівнює 1, оскільки вони є взаємовиключними і тільки один з них повинен здійснитися. Одні сценарії є більш ймовірними, інші - менш імовірними. Для того щоб вибрати найбільш ймовірні сценарії, розроблені методи, що дозволяють їх ранжувати.

1. Модель переливу капіталу
   Нехай інвестор стоїть перед вибором: інвестувати в Росію або в США. Ставка відсотка (прибутковість інвестицій) в Росії дорівнює /, в США - / *, плаваючий курс долара: поточний - е } очікуваний через рік - е ь . Для розрахунку доходу від рублевих інвестицій в США їх величину ділять на початковий
2. Модель олігархії
   Олігархія - економічна система, в якій уряд діє в інтересах групи приватних підприємців і не враховує інтереси інших груп населення. Воно встановлює ставку податку, яка найбільш вигідна для приватного бізнесу. Цільова функція уряду при олігархії - віддача на одиницю капіталу після вирахування
3. Модель міжнародного обміну (Хекшер - Олін)
   У країні виробляють тканину (х) і хліб (У) з праці (L) і землі (7), виробничі функції задані формулами (10.11). У кожній галузі сумарна вартість ресурсів дорівнює фіксованій величині витрат: де w иг - ціни праці і землі; R i і R 2 - витрати на ресурси в галузях. Обмеження для економіки в цілому:
4. Модель маленької країни при мінливому рівні цін
   Щоб продовжити графічний аналіз наслідків стабілізаційної політики при змінному рівні цін, доповнимо модель IS - LM - FE моделлю взаємодії сукупних попиту і пропозиції у відкритій економіці y D (P t е ) - y s (P f е) у в яку теж додамо третю лінію - лінію нульового сальдо торгового балансу
5. Модель Калдора
   Н. Калдор перетворив норму заощаджень в ендогенний параметр на основі наступних припущень: ? одержувачі прибутку (П) зберігають велику частину свого доходу, ніж одержувачі заробітної плати (І 7 ); ? ціни факторів виробництва, а отже, і величини прибутку і зарплати реагують на співвідношення
6. Моделі світової економіки, модель конкурентних переваг
   Нехай країна виробляє два продукти (X, Y). Виробнича можливість - набір випусків продуктів (Х, у), який країна може зробити при заданих технологіях і доступних обсягах ресурсів (х - випуск продукту Х } у - випуск продукту У). Кордон виробничих можливостей - підмножина виробничих можливостей
7. Моделі регулювання
   Порівняльна характеристика альтернативних цілей монетарної політики представлена в табл. 9.17. У 1990-х рр. Банк Росії орієнтувався більшою мірою на динаміку номінального ВВП і валютного курсу. Стримування зростання грошової маси з метою стабілізації валютного курсу рубля було головним напрямком
8. Модель Гудвіна
   У закритій економіці без економічної актив- пости держави завдяки гнучкій системі цін на ринку благ постійно існує рівновага; відповідно обсяг інвестицій дорівнює обсягу заощаджень. Внаслідок зростання населення і технічного прогресу національний дохід країни щорічно збільшується. Річний темп