
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Для математичного виразу міжгалузевого балансу інформацію про витрати на виробництво в окремих галузях, про транспортні торгово-посередницьких націнки, а також дані про податки, що входять в вартісну величину кожного міжгалузевого потоку, позначимо через Ху (Використовуємо в якості поточних витрат), а кожну компоненту продукції, що йде на потреби кінцевого споживання, через yik. З урахуванням введених позначень балансові тотожності для кожного рядка i запишемо у вигляді

де X / - обсяг випуску в галузі г; У, - кінцеве споживання.
Ці співвідношення є вихідними для побудови математичної моделі МОБ.
Отже, Xjj - це витрати продукції виду i на виробництво продукції виду j. З теоретичних міркувань слід, що обсяг витрат повинен бути позитивно пов'язаний з обсягом випуску Хр т. е.

Найпростіше і разом з тим найочевидніше (але не обов'язково точне) припущення щодо виду функції (8.3) полягає в прийнятті гіпотези про прямий пропорційності витрат і випуску в рамках окремої галузі, або

де atj за змістом - питома витрата матеріальних ресурсів виду i на виробництво одиниці продукції виду 7, або коефіцієнт прямих витрат па виробництво продукції. сукупність коефіцієнтів аху що стоять в однойменному стовпці, є формальним описом технології виробництва даної галузі /
В. Леонтьєв розглядав припущення про прямий пропорційної зв'язку витрат і випуску як допустимий спрощення реальних виробничих зв'язків, яке забезпечує простоту розрахунку коефіцієнтів а1} на основі звітних даних міжгалузевої таблиці.
Очевидно, що на розрахункові значення коефіцієнтів аУ) впливає і склад випуску Xj, і склад окремих потоків хху якщо Х-} і х ^ описують будь-якої виробничий процес (наприклад, виробництво сталі в електропечі, транспортування газу по трубопроводу і т. н.), незмінність технічних характеристик обладнання, що застосовується закономірно повинна визначати приблизну пропорційність витрат і випуску. Тому чим більше однорідним є склад продукції, що включається в дану галузь, і чим ближче виробничий процес, описуваний в термінах «витрати - випуск», до конкретної технології, тим більш обгрунтовано припущення про незалежність ахх від обсягу виробництва Ху
Саме ця обставина визначає необхідність складання міжгалузевої таблиці в розрізі «чистих» галузей, а також застосування можливо більш детальної галузевої класифікації. В умовах науково-технічного прогресу більш-менш достовірно коефіцієнти прямих витрат aXj можна оцінити не більше ніж на 5-7 років вперед.
коефіцієнти аХ) в сукупності утворюють квадратну матрицю А, або матрицю коефіцієнтів прямих витрат МОБ.
матрицю А іноді також називають матрицею технологічних коефіцієнтів, і вона допомагає побачити, як функціонує економіка. Якщо переважають сировинні продукти з невеликим ступенем переробки у вітчизняній економіці, в А присутній відносно небагато елементів, що значно відрізняються від нуля. У міру розвитку економіки, коли переробка сировини стає більш поширеною, в А з'являється більше записів, що відображають зрослу вертикальну і горизонтальну інтеграцію економічної діяльності.
Досліджуючи різні галузі, пов'язані з різними стадіями виробничого процесу, можна зрозуміти, де створюється додана вартість. Наприклад, бавовна вирощується як сільськогосподарська культура. Потім його ділять на бавовняне волокно і насіння (хлопкоочістка), бавовняне волокно далі перетворюють в нитки, а нитки - в тканини. Якщо кожен з цих видів діяльності здійснюється в різних галузях, можна зрозуміти, де між вирощуванням бавовни і отриманням в результаті тканини, для якої він використаний, створюється додана вартість.
У векторно-матричних позначеннях
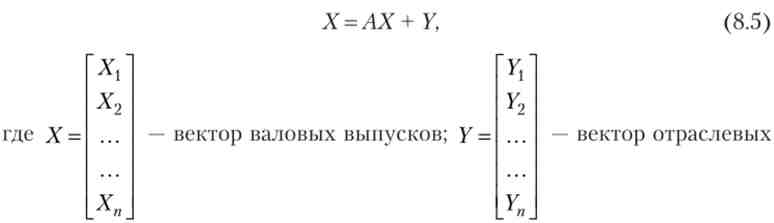
елементів кінцевого попиту.
Рішення системи (8.5) має вигляд

де Е - одинична матриця. Елементи матриці В = (Е - Л)-1 називаються коефіцієнтами повних витрат на виробництво кінцевої продукції, або коефіцієнтами повних витрат. Коефіцієнти повних витрат (Ь $) показують потребу у валовому випуску продукції галузі г для виробництва одиниці кінцевого попиту j-го виду. Кожен такий коефіцієнт враховує складний комплекс взаємозв'язків процесу виробництва. Формалізоване обгрунтування цього факту полягає в наступному.
З лінійної алгебри відомо, що якщо існує матриця (Е - Л)-1, зворотна матриці (Е - Л), то вона подана в вигляді нескінченного матричного ряду (Е + Л + Л2 + Л3 + ...) і відповідно
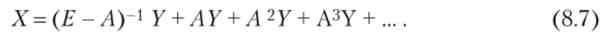
Дана система являє вектор валових випусків X як суму векторів, що характеризують послідовне зростання витрат продуктів галузей, пов'язаних з виробництвом встановленої кількості кінцевих продуктів. Перший доданок системи відображає той факт, що У - частина загальної суми валового продукція. У свою чергу, виробництво цих заданих кількостей кінцевих продуктів вимагає певних витрат матеріальних ресурсів різного галузевого походження; потреба в цих матеріальних ресурсах визначається величиною Л У; забезпечення виробничих потреб на виробництво продукції в розмірі AY, в свою чергу, викликає додаткову потребу в матеріальних ресурсах в розмірі Л (Л У) і т. д.
Співвідношення коефіцієнтів прямих і повних витрат має вигляд
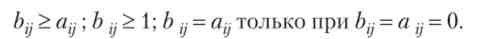
Нижче наведені деякі аналітичні і прогнозні завдання, які вирішуються за допомогою моделі МОБ.
За зміною елементів матриці А від року до року (якщо є така інформація) можна судити про зміну виробничих потреб в окремих видах матеріальних ресурсів. Так, зростання (зниження) питомих витрат палива па транспорті або в електроенергетиці, що виражається в зростанні (зниженні) відповідних коефіцієнтів прямих витрат, свідчить при інших рівних умовах про зниження (зростання) ефективності функціонування названих виробництв. Разом з тим зміни в технічних методах виробництва можуть бути такі, що зниження одних коефіцієнтів може супроводжуватися зростанням інших (наприклад, заміна лісу металом в будівництві, металу пластмасами в машинобудуванні і т. П.).
схема X = АХ + У дозволяє дати загальну оцінку цих змін. Зокрема, сума коефіцієнтів матриці А по стовпцю характеризує загальний рівень поточної матеріаломісткості виробництва (т. е. загальну потребу в матеріальних ресурсах на виробництво одиниці продукції) даного виду. Відповідно, звітні дані про загальний рівень матеріаломісткості в зіставленні з перспективними значеннями цього показника дозволяють робити висновки про тенденції і результати технічних змін в окремо взятій галузі або в економіці в цілому.
Схема балансу міжгалузевих зв'язків у вигляді X = АХ + У - найбільш проста його різновид - називається відкритої статичної моделлю.
Відкритої вона називається тому, що для визначення валових випусків (наприклад, перспективної виробничої програми народного господарства) необхідно екзогенне завдання вектора кінцевого попиту, т. Е. Попереднє знання обсягів та галузевого розподілу продукції, що використовується на споживання і накопичення.
Статичної модель є тому, що фіксує міжгалузеве розподіл проміжного продукту і окремі напрямки використання кінцевого попиту для даного року, не зв'язуючи явно поточний стан економіки з її попереднім станом.
Характерна риса динамічних міжгалузевих моделей в порівнянні зі статичними - відображення в них інвестиційного процесу. Дійсно, капітальні вкладення є носієм економічної динаміки і сполучною ланкою відтворювальних циклів.
Елементи кінцевого попиту - накопичення (інвестиції) і невиробниче споживання в статичної моделі задаються екзогенно. Однак з точки зору повноти аналізу відтворювального процесу необхідно перш за все врахувати взаємозв'язку інвестицій та обсягів виробництва.
Найбільш простий і історично перший спосіб формалізації зв'язків між галузевими обсягами випуску продукції та інвестиціями (також запропонований В. Леонтьєвим) - включення в схему балансу (поряд з йу - коефіцієнтами прямих матеріальних витрат) галузевих коефіцієнтів питомої капіталомісткості kh), або співвідношень виду

де AXj - приріст випуску в галузі j але порівняно з попереднім періодом часу (наприклад, роком); // у - обсяг інвестицій в основний капітал в галузь j> є продукцією галузі h. індекс h відноситься в даному випадку до так званим фондосоздающім галузям, т. е. галузям, продукція яких використовується в якості елементів капіталовкладень (в укрупненому МОБ таких галузей дві - машинобудування та будівництво).
якщо коефіцієнти khj передбачаються незалежними від інших змінних моделі (як і коефіцієнти прямих витрат), то окремі галузеві компоненти загального обсягу накопичення основного виробничого капіталу, що фігурують в II квадранті статичної моделі МОБ, можуть бути параметризовані у вигляді функцій, аргументами яких є галузеві прирости випуску продукції і коефіцієнти капіталоємності . В результаті система рівнянь, що описують розподіл продукції окремих галузей, буде включати як показники валових випусків поточного року, так і їх прирости але порівняно з попереднім роком. Тим самим рівняння МОБ стають динамічними, т. Е. Пов'язують галузеві показники виробництва, що відносяться до послідовних тимчасових інтервалах (років).
Всі відомі і практично апробовані моделі динамічного МОБ (як в Росії, так і за кордоном) є розвитком описаної схеми.
В рамках динамічного МОБ галузеві капіталовкладення виявляються внутрішніми (ендогенними) змінними моделі; інші ж елементи продукції, що надходить в кінцеве споживання, як і в статичному МОБ, повинні визначатися екзогенно. Тому в більш загальному контексті розвиток міжгалузевих моделей як інструменту економічних досліджень неминуче пов'язане з процесом трансформації показників III квадранта в показники II квадранта МОБ, в тому числі узгодження оцінок оплати праці та особистого споживання, обсягів інвестицій з галузевими розмірами прибутку і амортизації, т. Е. накопичень окремих галузей (прикладом подібної міжгалузевої моделі може служити модель для середньострокового економічного планування, розроблена в 1960-і рр. в Японії).
Моделі є динамічними моделями міжгалузевого балансу, якщо вони враховують такі взаємозв'язки:
можливості розвитку виробництва в даному році обумовлюються готівковим обсягом основних виробничих фондів, частина якого утворена фондами, введеними в попередні роки.
Розглянемо основні аспекти побудови прогнозу структури національної економіки виходячи з статичної моделі «Витрати - Випуск».
Опис економіки за допомогою моделі МОБ дозволяє розбити всю процедуру формування прогнозних показників на три складові: