| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
У параграфі 11.4 була відзначена взаємозалежність між розміром державного боргу і темпом економічного зростання. Неокласична модель росту дозволяє поглибити аналіз зазначеної взаємозалежності. Для цього в модель потрібно запровадити економічну активність держави.
Нехай державні витрати становлять певну частку (А) національного доходу G-ay і фіксована їх частина (b) Направляється на інвестиції (Ig) на додаток до інвестицій приватного сектора Ig = BG = aby. Податки стягуються за єдиною ставкою (Ту) з доходів від господарської діяльності, продажу праці та відсотків на державні облігації (5), що представляють державний борг: Т = Ту(у + ГВ). Загальний дефіцит державного бюджету (8) перевищує первинний дефіцит на величину виплат відсотків по державному боргу: 8 = G - Т + 1В. Якщо державний бюджет дефіцитний, то інвестиції приватного сектора менше його заощаджень на величину бюджетного дефіциту I = S- 8 = S- G + T-iB. Обсяг заощаджень приватного сектора дорівнює нормі заощаджень (s), помноженої на наявний дохід, що залишається після сплати податків: 5 = 5 (1 - Т) (у + iB). Трудові ресурси збільшуються з екзогенно заданим темпом приросту п. Для спрощення відвернемося від амортизації, і тоді приріст капіталу дорівнює обсягу приватних і державних інвестицій:
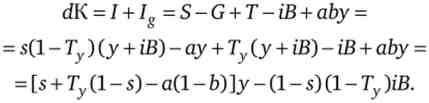
Щоб зменшити число змінних, запишемо це рівність в розрахунку на одного працюючого, взявши до уваги, що y / N = q = Ц /а і d| / = dK / N - т | /. Крім того, приймемо, що ставка відсотка дорівнює граничної продуктивності капіталу: i = ду / ДК = Ац /а_1, і позначимо B / N = Тоді приріст капіталоозброєності праці можна представити у вигляді
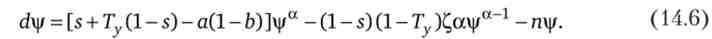
Нелінійне диференціальне рівняння (14.6) описує динаміку капиталовооруженности праці в даній моделі; звернемо увагу на те, що вона залежить і від величини державного боргу, представленого ф Для отримання рівняння, що описує динаміку державного боргу, врахуємо, що приріст держборгу дорівнює дефіциту бюджету: dB = 5 = (а - - Ту) У + (1 - Ty) IB, а приріст держборгу (облігацій) на одного працівника, на зразок приросту капіталу, дорівнює: dC, = dB / N - Гат тоді:
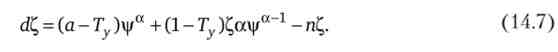
У стані динамічної рівноваги di = dC, = 0. Тому, прирівнявши рівності (14.6) і (14.7) до нуля, отримаємо систему з двох диференціальних рівнянь, рішення якої визначає значення і ф відповідні рівноважного росту:
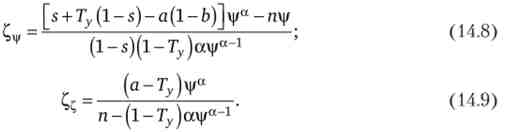
Рівняння (14.8) визначає все безліч поєднань i і ф при яких капиталовооруженность праці не змінюється в часі (ізокліни vp), а рівняння (14.9) - поєднання значень vp і ф при яких не змінюється частка державного боргу в національному доході в розрахунку на одного працівника (ізокліни Q.
Графічне рішення системи рівнянь (14.8) і (14.9) при значеннях a = 0,25; а = 0,22; b = 0,6; Ту = 0,2; s = 0,3; п = 0,03 представлено на рис. 14.10. ізокліни С, має розрив при значенні vp, що перетворює знаменник у виразі (14.9) в нуль.
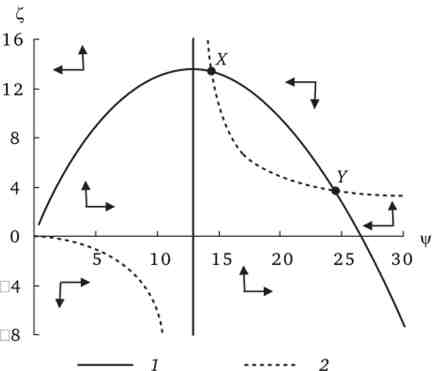
Мал. 14.10. Ізокліни капиталовооруженности праці (?) І частки державного боргу в національному доході на одного працівника (2)
З рис. 14.10 очевидно, що при наявності державного боргу (? > 0) існує не більше двох станів динамічної рівноваги. Ізокліни ділять все безліч нерівноважних поєднань | / і С, на п'ять підмножин, що розрізняються тим, в якому напрямку відповідно до рівняннями (14.8) і (14.9) будуть змінюватися розглядаються показники. З цього випливає, що в точці X (| / = 14,4;? = 13,2) рівновага є нестійким, а в точці Y (Р = 24,5; С, = 3,8) - стійким. Лише випадково рівноважна капиталовооруженность праці може відповідати «золотому правилу» накопичення капіталу.