Еластичність заміщення факторів виробництва і рівноважний зростання

Як уже зазначалося, умова стійкого зростання в моделі Солоу - Свана можна представити у вигляді наступного рівняння: so = n; в ньому екзогенно задані s і п, а а знижується в міру зростання капіталоозброєності праці

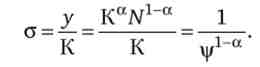
Тому графічно процес руху до стійкого економічного зростання можна змалювати таку картину, як показано на рис. 14.11. оскільки so-n = j), то відстань між зображеними на цьому малюнку лініями представляє темп приросту капіталоозброєності праці.

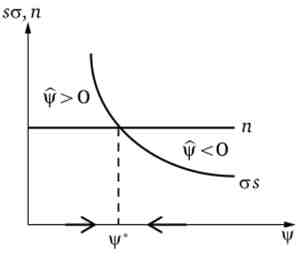
Мал. 14.11. Стійкість зростання в моделі Солоу - Свана

Так як п> 0, а а -> оо при | / -> 0 і а -> 0 при | / - »оо, то існує єдина точка стійкого рівноважного зростання з незмінними значеннями капиталовооруженности праці та продуктивності капіталу. Це - властивість технології, яка відображається виробничою функцією Кобба - Дугласа.

Специфіка технології (залежно витрати - випуск) характеризується еластичністю заміщення факторів виробництва

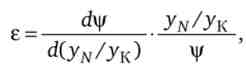
де е - коефіцієнт еластичності заміщення, який показує, на скільки відсотків повинна змінитися капиталовооруженность праці при зміні ставлення граничних продуктивностей праці і капіталу на 1%, щоб випуск не змінився. В технології Кобба - Дугласа 8 = 1.

У найбільш загальному вигляді технологія виробництва відображається виробничою функцією з постійною еластичністю заміщення

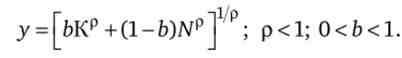
Еластичність заміщення факторів виробництва при такій технології визначається за формулою 8 = 1 / (1 - р). Коли р -> 0, тоді у -> у = AK^bl} ~^b; якщо р - » - оо, то у -> у = Min {bK, (l- b) N}.

Середня продуктивність капіталу при технології з постійною еластичністю заміщення факторів

якщо 0 < р < 1, т. Е. 8 > 1, то lima = Ь^{1 / р} > 0 і limso = sb^{1 / P} > 0.

J / -> оо

Якщо limsa = sb^{A р} > П, то на відміну від варіанту, представленого на

у- »оо

Мал. 14.11, крива so не перетинається з прямою п. Це означає, що при технології з 8 > 1 в зростаючій економіці встановиться динамічна рівновага з постійним темпом приросту капіталоозброєності і продуктивності праці.

приклад 14.4

У початковий період К = 80; N = 10; темп приросту населення п = 0,05; норма заощаджень 5 = 0,25; виробнича функція

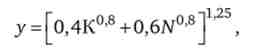
еластичність заміщення факторів виробництва якої дорівнює е = 1 / (1 - 0,8) = 5. Динаміка економічних показників в умовах неокласичної моделі зростання представлена на рис. 14.12 і в табл. 14.9.

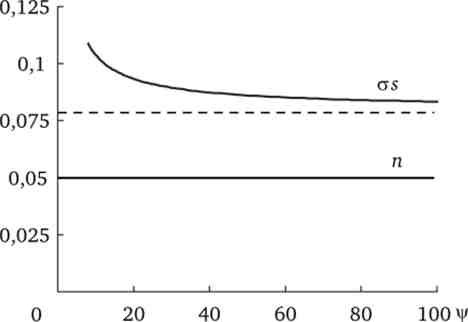
Мал. 14.12. Рівноважний зростанні зростаючої КАПИТАЛОВООРУЖЕННОСТЬ праці

Таблиця 14.9. Динамічна рівновага при зростаючої капиталовооруженности і продуктивності праці

Якби технологія виробництва національного доходу відображалася виробничою функцією

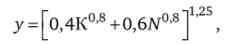
еластичність заміщення факторів виробництва якої дорівнює е = 1 / (1 + 0,8) = 0,56, то динамічна рівновага встановилося б при стабільних значеннях q = 1,636; у = 8,181 (рис. 14.13 і табл. 14.10).

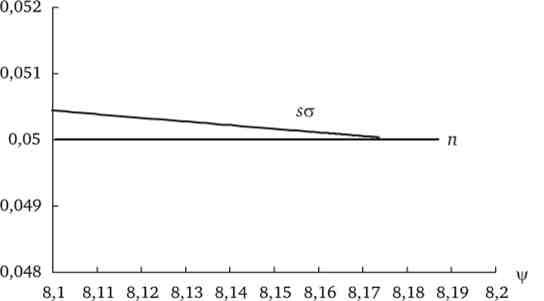
Мал. 14.13. Динамічна рівновага при технології, яка відображається виробничою функцією CES з постійною КАПИТАЛОВООРУЖЕННОСТЬ праці

Таблиця 14.10. Динамічна рівновага при технології, яка відображається виробничою функцією CES з постійною КАПИТАЛОВООРУЖЕННОСТЬ і продуктивністю праці

1. Хайєковські форми і кейнсіанські розміри
   Англійської аудиторії було чуже використання трикутної конструкції в якості основи для макроекономічного теоретизування, зокрема для пояснення природи підйомів і спадів. Спроба Хай- ска уявити теорію циклічного зміни виробництва за допомогою трикутників і з урахуванням межчасовий переваг спочатку
2. Характеристики нульового порядку, характеристики першого порядку
   Кожній функції / зіставляються її значення в спостерігалися точках х (?) = (Х, (?)> х "{()). Дана характеристика відображає наявність у функції асимптот і показує, який максимальний обсяг випуску при необмеженому зростанні одного з факторів (якщо Х2 / обсяг випуску необмежено зростає). Значення
3. Грошовий мультиплікатор
   Повна модель мультиплікації грошей будується з урахуванням відтоку частини грошей з депозитів у готівку. Грошова база (гроші підвищеної потужності) (В) - це банківські резерви (R ) Плюс готівку, яка звертається поза банками (С): Уподобання населення щодо форми зберігання грошей впливають
4. Глобалізація і національна економіка, сучасне світове господарство
   В результаті вивчення даного розділу студент повинен: знати - ключові компоненти глобальної економіки; вміти - аналізувати форми прояву інтерналізації господарського життя в національній економіці; володіти - навичками дослідження різних підходів до розуміння сутності та основних рис процесів
5. Гіпотеза Фріша - Слуцького
   Гіпотеза Фріша - Слуцького є основою для економетричного аналізу бізнес-циклів. Вона показує, чому і як виникає бізнес- цикл. Відповідно до гіпотези існують імпульси, поширення яких запускає бізнес-цикл, сприяє зростанню економіки або її падіння. Наведемо приклади. Спусковим механізмом іпотечної
6. Гедонічні індекси
   Більш загальним і ефективним методом вирішення проблем, пов'язаних зі змінами якості, є використання оціночних значень цін, одержуваних з гедоничних регресійних рівнянь. Гедонічні регресивні рівняння пов'язують спостережувані ринкові ціни різних моделей товарів з певними ціноутворюючими
7. Функція Кобба - Дугласа
   Тут також використовується кілька систем передумов, що виділяють клас функцій Кобба - Дугласа серед двічі диференційовних функцій від двох змінних: а) еластичності випуску за факторами постійні: Рішенням цієї системи диференціальних рівнянь в приватних похідних першого порядку є клас функцій
8. Фіскальна стійкість, сеньйораж і інфляція
   В результаті вивчення матеріалу даного розділу студент повинен: знати визначення платоспроможності; фактори, що впливають па платоспроможність держави в короткостроковій і довгостроковій перспективі; поняття сеньйоражу стосовно способів фінансування державного боргу; модель Кейган (учасники