2.9.2. Лінійне програмування
Метод лінійного програмування, найбільш поширений в прикладних економічних дослідженнях зважаючи на його досить наочною інтерпретації, дозволяє господарюючому суб'єкту дати обгрунтування найкращому (за формальними ознаками) рішенням в умовах більш-менш жорстких обмежень, що стосуються доступних для підприємства ресурсів. За допомогою лінійного програмування в аналізі фінансово-господарської діяльності вирішується цілий ряд завдань, в першу чергу відносяться до процесу планування діяльності, який він дозволяє відшукувати оптимальні параметри випуску і способи найкращого використання наявних ресурсів.
Суть методу лінійного програмування полягає в пошуку максимуму або мінімуму обраної відповідно до інтересів аналітика цільової функції при наявних обмеженнях. Розглянемо використання цього методу на прикладі 2.15.
Приклад 2.15. Фабрика з виробництва чаю випускає дві марки цього продукту. Умовне найменування марок - А і В. Відпускна ціна чаю марки А - 60 руб. за кілограм, марки В - 50 руб. за кілограм. Якими мають бути оптимальні річні обсяги виробництва чаю обох марок, щоб виручка фабрики від їх реалізації був максимальним?
Нехай оптимальний обсяг виробництва чаю марки А складе X тонн на рік, а марки В - у тонн на рік. Сумарна виручка від їх реалізації складе (60x + 50y) тис. руб. Рішення завдання передбачає пошук такої комбінації (х, у), яка дозволила б забезпечити максимум цієї функції, тобто пошук
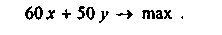
Зрозуміло, що чим більше буде випуск і тієї, і іншої марки, тим більше буде виручка, проте ресурси фабрики небезмежні. Для виготовлення обох сортів чаю використовується одне і те ж обладнання, загальна продуктивність якого становить 300 тонн продукції на рік. Таким чином, обмеження по потужності обладнання виглядає наступним чином:
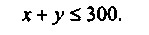
При виготовленні чайних сумішей різних марок використовують чайний лист двох сортів: до складу чаю марки А входить 70% 1-го сорту і 30% 2-го сорту, до складу марки В - 20% 1-го сорту і 80% 2-го сорту.
Фабрика може витрачати на закупівлю сировини не більше 9000 тис. руб. на рік. Отже, на обсяг випуску накладається ще одне обмеження фінансового порядку:
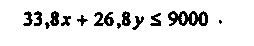
Зрозуміло, що шукані величини обсягів виробництва різних сортів чаю (x і у) повинні бути позитивні. Таким чином, повна формулювання задачі лінійного програмування в даному випадку буде наступною:
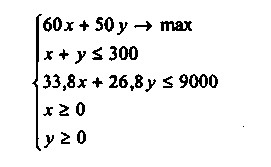
Для вирішення цього завдання знайдемо область можливих значень х і у графічним способом (рис. 2.3). Для цього спочатку знайдемо на площині (х, у) область, що відповідає всім чотирьом обмеженням.
Пошук рішення задачі лінійного програмування
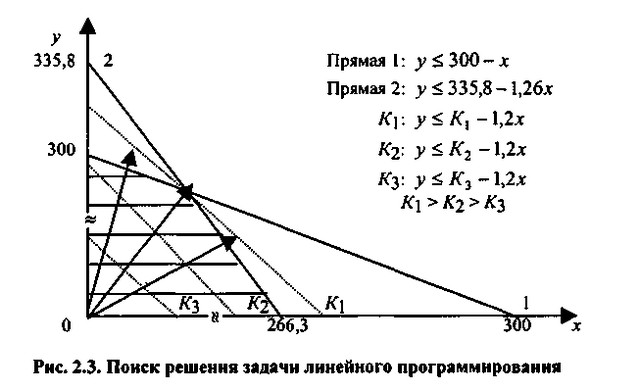
На рис. 2.3 пряма 1 відповідає виробничому обмеженню, пряма 2 - фінансовому; двох залишилися обмеженням відповідають самі осі х і у. Таким чином, задовольняють всім обмеженням значення (х, у) лежать в заштрихованої області. Яка ж точка цього п'ятикутника буде шуканим рішенням? Нам потрібно знайти таке значення К, яке дозволило б максимізувати цільову функцію на заштрихованої області. Для цього розглянемо безліч функцій виду
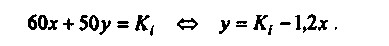
Три з цих функцій наведено на рис. 2.3 пунктирними прямими. Чим далі у напрямку стрілок від центру координат знаходиться пряма, тим більшому значенню Кi вона відповідає. Очевидно, що на заштрихованої області функція (60x + 50У) прийме максимальне значення в точці перетину прямих 1 і 2. Отже, координати цієї точки будуть шуканим оптимальним рішенням, максимизирующим цільову функцію.
Найденное алгебраїчним методом рішення цієї системи рівнянь буде таким:
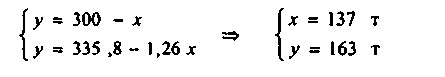
Саме таке співвідношення обсягів випуску чаю сортів А і В дозволить фабриці при існуючих технологічних і фінансових обмеженнях отримати максимальний обсяг виручки .
Існує безліч комп'ютерних програм, що дозволяють відшукувати рішення в задачах з десятками і навіть сотнями параметрів і обмежень. Розглянутий нами в прикладі 2.15 випадок представляв собою завдання оптимізації випуску при двухпродуктовом виробництві (марки А і В). Реальні ж підприємства в переважній більшості випадків випускають набагато ширшу номенклатуру продукції, залучаючи при цьому у виробництво не два, як у прикладі 2.15 (1-й і 2-й сорту), а сотні й тисячі видів різних ресурсів. Обмеження можуть стосуватися не тільки технологічних і фінансових можливостей підприємства (т.
Крім задачі оптимізації випуску, не можна не згадати ще про два типи завдань, які вирішуються за допомогою методу лінійного програмування: це так звані транспортні завдання і завдання складання розкладу.
Тисячам підприємств, великих і малих, доводиться щодня вирішувати проблему, як найкращим способом доставити товар споживачам, що знаходяться на різних відстанях і в різних напрямках від підприємства, та ще з урахуванням обсягу замовленої партії товару. Постановку транспортної задачі можна описати як мінімізацію витрат на експлуатацію транспортних засобів при існуючих обмеженнях на наявне їх кількість, вантажопідйомність, тривалість робочого дня при необхідності обслужити якомога більшу кількість замовлень.
Завдання складання розкладу полягає в такому структуруванні часу роботи колективу підприємства, яке було б максимально зручно для всіх його співробітників і клієнтів. Особливо актуальна ця проблема для підприємств сфери послуг, а також освітніх установ. Наприклад, якщо відомо, що максимальна кількість покупців приходить в магазин з 15 до 19 годин по буднях і з 11 до 16 годин по суботах і неділях, то і кількість співробітників, чиї робочі години припадають на цей час, має відповідати напливу клієнтів. Графік роботи змін повинен забезпечувати максимальну чисельність персоналу в торговому залі саме в ці години. Складання графіка роботи співробітників на таких підприємствах можна вважати задачею лінійного програмування. Типова постановка задачі лінійного програмування в даному випадку така: максимізація кількості обслужених покупців при наявних обмеженнях, що стосуються кількості співробітників, а також з урахуванням вимог законодавства з приводу тривалості робочого дня і кількості вихідних днів на тиждень для кожного співробітника.
В аналізі розміщення та використання ресурсів і в процесі планування метод лінійного програмування знаходить досить широке застосування.
У всіх розглянутих нами випадках ми вважали, що залежності між факторами лінійні і характер їх не змінюється з часом. Це далеко не завжди буває так, тому в теорії прийняття рішень використовуються також методи нелінійного, динамічного, стохастичного, опуклого програмування, які набагато більш складні і застосовуються в аналізі діяльності окремих підприємств вкрай рідко.
Інформація, релевантна " 2.9.2. Лінійне програмування "
- Терміни і поняття
програмування Великі цикли Н. - 25. ОТЕЧЕСТВЕННАЯЕКОНОМІКО-МАТЕМАТИЧНА ШКОЛА.Л.В. КАНТОРОВИЧ: ЛІНІЙНЕ ПРОГРАМУВАННЯ
лінійного - 91. Л. В. Канторович: розробка теорії лінійного програмування
лінійного програмування Леонід Віталійович Канторович (1912-1986) був (спільно з американським економістом Т. Купмансом) удостоєний Нобелівської премії в галузі економіки (1975 р.) . Заслуга Канторовича полягає в тому, що він запропонував математичний метод пошуку оптимального варіанту розподілу ресурсів. Вирішуючи конкретну задачу досягнення найбільшої продуктивності при завантаженні - 3.2. Лінійні чарти (Line Charts)
лінійний "так, як ми його сприймаємо в російській мові, не зовсім коректно. Цей тип скоріше можна назвати" графіком відрізків ", але ми за вже сформованою у російських фахівців традиції будемо називати його "неправильним" ім'ям. 8 На підставі щоденного фіксингу на ММВБ. 34 35 Рис. 3.3. Графік руху курсу Долар США / Російський рубль за даними про щоденний фіксинг. - 18.3. КЛАСИФІКАЦІЯ СТРУКТУР УПРАВЛІННЯ
лінійна структура управління? підпорядкованість знизу вгору, вона використовується в невеликих фірмах з однорідною і нескладною технологією, б) лінійно-штабна структура? створення спеціалізованих служб (штабів) при кожному лінійному керівнику; наприклад, штаб для : 1) організації випуску нової продукції; 2) реалізації інноваційних проектів; 3) реалізації стратегії підвищення якості і т. д.; в) - Лінійні залежності
лінійної; це означає, що лінія, що представляє цю залежність, є прямой.Чтоби побудувати графік лінійної залежності, нам треба знати тільки дві величини: значення вільних члена і значення кутового коеффіціента.Еслі значення X розташовані на горізонтальнойосі, а значення У - на вертикальній, як на ріс1П-1, то вільний член визначається значенням Yпрі X=O. Отже, графічно - 10.2. Попит і виручка
лінійної функції попиту відповідає і лінійна функція граничної виручки (рис. 4.10). Зупинимося на цьому відповідно докладніше, оскільки воно широко використовується при аналізі монополії, коли функція граничної виручки набуває особливо важливого значення. Припустимо, що попит на продукцію монополіста заданий лінійною функцією: Q=a - bP, (10.5) де а, b - позитивні константи. На - Програма. Ще про криві попиту та еластичності попиту за ціною
лінійних крівихспроса полягає в тому, що їх легко будувати і анали -зировать. 94 Частина 2: Попит, пропозиція і ринки товарів Кількість (а) Кількість (Ь) РИС. 5П-1. Нелінійні криві попиту, (а) Криві попиту з постійною еластичністю. (Ь) Крива попиту з високою еластичний-ністю при низькій ієни і низькою еластичністю при високій ієни (крива попиту із зворотного - 2.1.2 Економічне програмування в країні
програмування призначене для координування між собою всіх форм державного втручання в економічне життя і є напрямних початком у господарському розвитку країни. Програмування, чи планування, економіки складалося і розвивалося в Італії протягом усього післявоєнного періоду, йдучи часткових форм до більш широким. Число діяли часткових планів було - 4 . Неокласична модель зростання Р. Солоу
лінійно-однорідну виробництві ^ ную функцію: Y=F {K, L). Розділивши всі члени на L і позначивши дохід на одного працюй! (У / L) через у, а капіталоінтенсіЕНОсть K / L через к, отримаємо: y=LF (k, \)=L №. Як і в моделі Харрода-Домара, передбачається, що населення зростає незмінним темпом і, а інвестиції становлять постояннун частку доходу, яка визначається нормою заощадження s: I=sY. Темп - Контрольні питання
програмування як інструментів економічного регулювання? 8. Що таке перехідна економіка? 9. Які основні напрямки формування ринкової економіки в перехідний період? 10. Що таке приватизація і які способи приватизації ви знаєте? 11. У чому виявляються основні негативні елементи державного втручання в економіку? 12. У чому полягає дерегулювання - 47. ВНУТРІШНЯ середу ПІДПРИЄМСТВА
лінійна структура; 2) цільова структура. Кожній відповідає однойменна система управління. Лінійна система обеспечіваетуправленіе по лінії прямого підпорядкування зверху вниз. Через цю систему керівники доводять до кожного виконавця свої розпорядження і здійснюють контроль за їх виконанням. При лінійному управлінні кожен вищестоящий керівник є прямим начальником усього