2.7.3. Елементарні методи обробки розрахункових даних
Зрозуміло, всі середні величини відносяться до першої групи показників, оскільки є характеристиками досліджуваної сукупності як цілого. Крім того, в якості показників спільності використовуються такі величини: середина інтервалу, мода і медіана.
Середина інтервалу можливих значень xi розраховується за формулою:
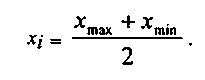
Мода - таке значення досліджуваного ознаки, яке серед всіх його значень зустрічається найчастіше. Якщо частіше інших зустрічаються два або більше різних значень, таку сукупність даних називають бімодальною або мультимодальной. Якщо ж ні одне із значень не зустрічається частіше за інших (тобто якщо всі значення зустрічаються по одному разу або рівну кількість разів), така сукупність є безмодальной.
Медіана - таке значення досліджуваної величини, яке ділить досліджувану сукупність на дві рівні частини, в яких кількість членів зі значеннями менше медіани дорівнює кількості членів, які більше медіани. Медіану можна знайти тільки в сукупностях даних, що містять непарну кількість значень. Тільки тоді і зліва, і справа від медіанного значення буде однакове число членів.
На відміну від середньої, величина медіани не залежить від крайніх значень показників. Наприклад, якщо максимальне значення досліджуваного показника збільшиться, то всі середні зростуть разом з ним, медіана ж залишиться незмінною. Тому вона є більш зручною характеристикою сукупності в тих випадках, коли сукупність даних неоднорідна і має різкі "викиди" у бік мінімуму або убік максимуму.
Як показники розмаху та інтенсивності варіації показників найчастіше використовуються такі величини: розмах варіації, середнє лінійне відхилення, середньоквадратичне відхилення, дисперсія і коефіцієнт варіації.
Розмах варіації розраховується за формулою:
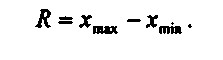
Середнє лінійне відхилення (середній модуль відхилення) від середнього арифметичного обчислюється за формулою:
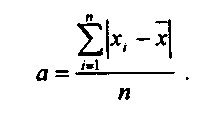
Якщо використовуються вагові коефіцієнти, то формула середньозваженого середнього лінійного відхилення має вигляд:
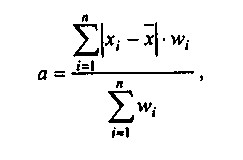
де wi - частота, з якою в досліджуваної сукупності зустрічається значення xi.
Найбільше поширення при вивченні розкиду значень числових даних отримали величини середньоквадратичного відхилення (СКО)? і дисперсії? 2:
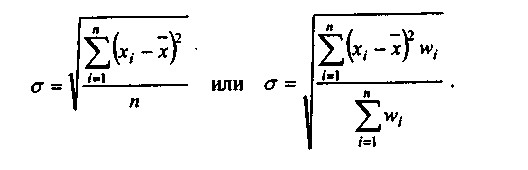
Чим більше величина? або? 2, тим сильніше розкид значень навколо середнього. Слід зазначити, що? завжди більше модуля середнього лінійного відхилення. Для нормально розподілених величин? / А 1,2. Якщо ж таке співвідношення не виконується, це свідчить про те, що в досліджуваному масиві даних є елементи, неоднорідні з основною масою, сильно вибиваються за своєю величиною із загального ряду. Залежно від природи розв'язуваної задачі слід подумати про виключення цих одиниць з розгляду взагалі або не використовувати їх при побудові деяких моделей, оскільки вони є у своєму роді винятками із загального правила.
Величина СКО, як випливає з її визначення, залежить від абсолютних значень самого досліджуваного ознаки. Чим більше величини xi, тим більше буде?. Тому для порівняння рядів даних, що відрізняються за абсолютними величинами, вводять коефіцієнт варіації:
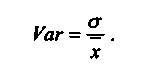
Цей коефіцієнт є показником "кількісної" неоднорідності сукупності даних. Критичне значення його вважається рівним 33%. Якщо VаR> 33%, то сукупність не можна визнати однорідною.
Використання коефіцієнта варіації в аналізі даних, що стосуються фінансово-господарської діяльності торгової мережі, розглянемо на прикладі 2.12.
Приклад 2.12. Торгова мережа "Океан" включає 10 магазинів та спеціалізованих відділів в універсамах міста. Є дані про виручку (R) і середньорічної вартості основних засобів (ОФ) кожного з магазинів за 1998 і 1999 рр.. (Тис. крб.). На підставі цих даних потрібно зробити висновок про посилення або зменшення ступеня диференціації точок у торговельній мережі за критерієм фондовіддачі (ФО).
Аналізовані дані представлені в табл. 2.4.
Таблиця 2.Показателі фондовіддачі торгових точок мережі "Океан"
Показники фондовіддачі торгових точок мережі "Океан"
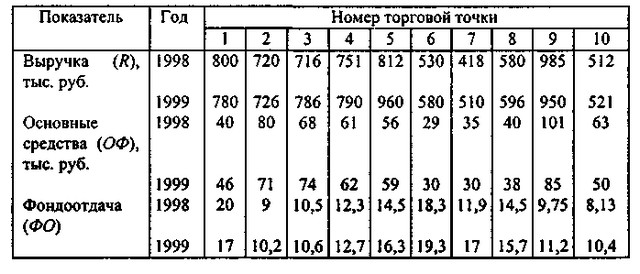
Потрібно порівняти показники фондовіддачі різних підприємств однієї торгової мережі за звітний і попередній роки.
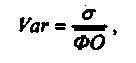

По зміні величини коефіцієнта варіації можна скласти думку про поглиблення диференціації магазинів або, навпаки, про підвищення однорідності торгових точок в мережі. Зокрема, спостерігається за аналізовані два роки зменшення коефіцієнта варіації фондовіддачі свідчить про підвищення однорідності різних магазинів мережі за цим критерієм.
Однією з найважливіших аналітичних характеристик є ступінь асиметрії розподілу, яка характеризується коефіцієнтом асиметрії:
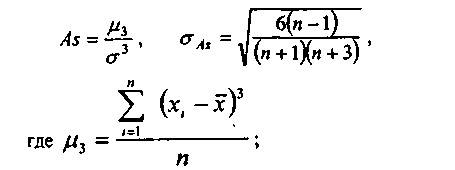
п - кількість спостережень.
Деякий розподіл симетрично в тому випадку, якщо As=0. Чим більше величина As, тим більше асиметрично розподіл величин.
Крутизна розподілу даних характеризується показником ексцесу:
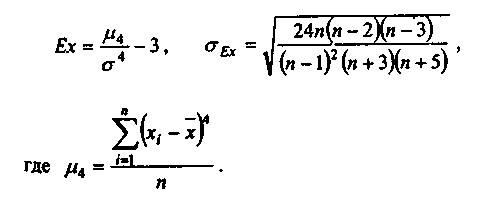
Для нормального розподілу Ех=0. Великий позитивний ексцес означає, що в сукупності даних є слабо варьирующее за цією ознакою "ядро", оточене рідкісними, сильно відстають від нього значеннями. Велике негативне значення показника ексцесу говорить про відсутність такого "ядра".
Розрахунок всіх розглянутих у даному розділі показників спільності і варіації, характеризують ряди даних, буде приведений у прикладі 4.13 (розділ 4.11).
Інформація, релевантна " 2.7.3. Елементарні методи обробки розрахункових даних "
- РЕЗЮМЕ
методологію, програми спостереження, а інші безпосередньо здійснюють збір, обробку та публікацію статистичних даних. Різноманіття статистичних збірників, що випускаються різними організаціями з різних сфер економічної діяльності, ставлять питання про уніфікацію методів збору інформації, її статистичній обробці, порівнянності класифікаторів, що беруть участь у міжнародному обміні - Ринковий підхід
методу оцінки: метод ринку капіталів, метод угод та метод галузевої оцінки. Метод ринку капіталів заснований на цінах продажу акцій подібних фірм на світових фондових ринках. Для застосування цього методу потрібно детальна фінансова і цінова інформація по представницької групі порівнянних фірм. Серцевина методу - фінансовий аналіз, вибір і обчислення оціночних коефіцієнтів (факторів). К - 2. МЕХАНІМЗ ОРГАНІЗАЦІЇ МІЖНАРОДНОЇ СТАТИСТИКИ
методів, однакових правил і програм спільних робіт. У розвиток цього міжнародного форуму було вирішено заснувати Міжнародний статистичний інститут - МСІ (InternationalStatisticalInstitute-ISI), який був створений в 1885 р. Відповідно до Статуту, основним завданням МСІ є розвиток та удосконалення статистичних методів у різних країнах світу. Фактично МСІ проводить курс на - Методи історико-економічного аналізу
методів пізнання, застосовуваних цією наукою, пов'язана з використанням методологічного арсеналу, категоріального апарату, основних теоретичних побудов історичного та економічного знання і відображає їх взаємодію. Методи, що застосовуються при історико-економічних дослідженнях, поділяються на традиційні та новітні. У систему традиційних методів входять: 1) історичний - Внутрішня норма прибутковості
метод розрахунку називається методом ітерацій. Додамо, що Вt - Сt як показник широко використовується при оцінці результатів діяльності фірми (підприємства) і називається грошовими надходженнями (грошовим потоком, англ. Cash flow). Він має більш широке значення, ніж надходження готівкових коштів до каси фірми (підприємства): це чистий грошовий результат комерційної діяльності фірми. - 2.3.2. Комп'ютерна обробка даних
методів у самих бухгалтерських та управлінських інформаційних системах не передбачено. Для цього існують спеціальні прикладні пакети аналізу. Хорошим прикладом такої аналітичної системи є пакет Statistica. Невеликий, але досить функціональний аналітичний пакет входить до складу табличного процесора MSExcel, що працює в середовищі Windows. Комп'ютери, що працюють з Windows, є - ОСНОВНІ ПОНЯТТЯ
методам розрахунків, які використовуються різними країнами, галузями і сферами господарства показників економічного розвитку з метою забезпечення їх - 2.8.4. Дисперсійний аналіз
метод, що дозволяє підтвердити або спростувати гіпотезу про те, що дві вибірки даних відносяться до однієї генеральної сукупності. Стосовно до аналізу діяльності підприємства можна сказати, що дисперсійний аналіз дозволяє визначити, до однієї і тієї ж сукупності даних чи ні відносяться групи різних спостережень. Дисперсійний аналіз часто використовується спільно з методами угруповання. - § 3. ЕКОНОМІЧНА ОЦІНКА ПІДВИЩЕННЯ ПРОДУКТИВНОСТІ ПРАЦІ ПО ФАКТОРАМ
методами прямого і факторного рахунку. Приріст продуктивності праці методом прямого рахунку визначається за формулою: де: - обсяг виробництва (реалізації) продукції в розрахунковому та базовому періодах; - чисельність персоналу відповідно в розрахунковому та базовому періодах. Для економічної оцінки підвищення продуктивності праці за методом факторного - 4.2 Характеристика виробничого процес а
елементарних технологічних процедур, що здійснюються при виготовленні готового виробу. Ці окремі процедури називаються операціями. Операція - це елементарна дія (робота), спрямоване на перетворення предмета праці й одержання заданого результату. Виробнича операція - це окрема частина виробничого процесу. Зазвичай вона виконується на одному робочому місці без - 20. ЕТАПИ МАРКЕТИНГОВИХ ДОСЛІДЖЕНЬ
методів проведення маркетингових досліджень, а розробку в рамках маркетингових досліджень специфічних завдань. На цьому етапі також визначається потреба в інформації, тип необхідної інформації, джерела і методи її одержання. 4. Збір даних. З точки зору організації процесу існує принаймні три альтернативних підходи до збору даних: силами співробітників маркетингової служби, - 2.5.3. Побудова аналітичних таблиць
обробки та отриманих результатів. Вона являє собою комбінацію горизонтальних рядків і вертикальних граф (стовпців, колонок). Остов таблиці, в якому заповнена текстова частина, але відсутні числові дані, називається макетом таблиці. Аналітичні таблиці використовуються на всіх етапах проведення аналізу фінансово-господарської діяльності: на етапі підготовки вихідних даних у таблиці