2.7.2. Метод угруповання даних
Найважливіше питання при проведенні такого роду дослідження - вибір інтервалу угрупування. Існують два основних підходи (методу) до його вирішення.
Перший підхід припускає розподіл сукупності даних на групи з рівними інтервалами значень. Цей метод використовується найбільш часто, так як він позбавлений суб'єктивізму при виборі кордонів інтервалів. При визначенні довжини інтервалу i доцільно користуватися формулами Стерджеса:
формула Стерджеса
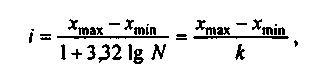
де хmах - максимальне значення ознаки в досліджуваній сукупності;
xmin - мінімальне значення ознаки в досліджуваній сукупності;
k - число груп;
N - число спостережень.
Цілком очевидно, що знаменник дробу чисельно дорівнює кількості груп або інтервалів, на яке розбивається вихідна сукупність.
Таким чином, оптимальна кількість груп, відповідне деякому числу спостережень, згідно з формулою Стерджеса можна представити таким чином:
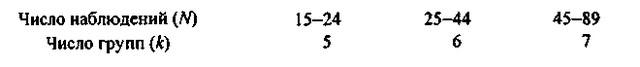
Пряме застосування формули Стерджеса означає, що на параметри угруповання не накладається яких обмежень. Можливий і варіант, коли такі обмеження вводяться, - наприклад, аналітик вже має деяке уявлення про число груп (зокрема, таке обмеження може бути викликано бажанням забезпечити деяку якісну однорідність виділяються груп одиниць сукупності). В останньому випадку довжина інтервалу угруповання знаходиться розподілом розмаху варіації, тобто різниці між максимальним і мінімальним значеннями группировочного ознаки, на передбачуване число груп.
Відповідно до другого підходу інтервали угруповання можна вибрати і нерівними (зростаючими або убутними). Цей підхід зазвичай застосовується при великій варіації і нерівномірності розподілу ознаки по всьому інтервалу його зміни. При виборі розміру інтервалу угруповання керуються здоровим глуздом і логікою, спираючись при цьому на розподілу минулих періодів і традиційно сформовані підходи в угрупованні. При використанні цього підходу інтервали часто вибирають таким чином, щоб групи були равнозаполненнимі.
Ілюстрація використання обох підходів до угруповання приведена в прикладі 2.11.
Приклад 2.11. Компанія "Фарма" володіє мережею стаціонарних аптек, аптечних кіосків та фармацевтичних відділів у різних магазинах міста. Виручка 35 торгових точок, що належать компанії, за липень 1999 р. склав (тис. крб.):

Використовуючи формулу Стерджеса, отримаємо:
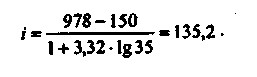
Округливши цей результат, в якості довжини інтервалу угруповання виберемо 140. Угруповання буде мати вигляд:

Угрупування, на думку аналітика, вийшла не надто вдала, оскільки не цілком відображає реальну структуру сукупності.
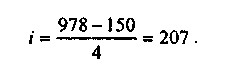
Округливши, візьмемо довжину інтервалу угруповання рівний 200. Тоді угруповання прийме вигляд:

Це угрупування вже набагато краще відповідає істинному стану речей.
Спроба застосувати підхід равнозаполненних інтервалів різної довжини ніякої змістовної інформації для аналізу в даному випадку не дасть. Формально таке угрупування могла б виглядати таким чином:

У цьому угрупованню інтервали, починаючи з другого, постійно збільшуються.
Як зазначалося вище, метод нерівних інтервалів достатньо обгрунтований у разі відчутною варіації группировочного ознаки. У цьому випадку застосування формули Стерджеса, що припускає певну рівномірність у розподілі значень группировочного ознаки всередині інтервалу варіювання, не дає логічно прийнятних результатів. При побудові нерівних інтервалів необхідно орієнтуватися на фактичний розподіл аналізованої сукупності і намагатися забезпечити достатню наповненість всіх інтервалів угруповання. Знаходження інтервалів може здійснюватися методом послідовних ітерацій.
У деяких ситуаціях при угруповання сукупності з відчутно варьирующим ознакою все ж можливе застосування формули Стерджеса. Уявімо собі ситуацію, коли торговельна фірма має 100 магазинів торговою площею, варьирующей від 10 до 400 кв. м, і два великих універмагу торговою площею відповідно 8000 і 12 000 кв. м. Якщо скористатися формулою Стерджеса, отримаємо:
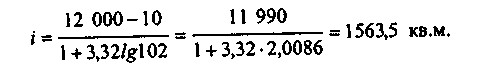
Вся сукупність, отже, повинна бути розділена на вісім груп, наприклад, такого вигляду:

Навряд чи така угрупування представляє інтерес для аналітика, оскільки переважна частина одиниць сукупності потрапила в один інтервал, а більшість інших інтервалів взагалі виявилися незаповненими. Тому з очевидністю напрошується висновок про необхідність відокремлення великих універмагів в окрему групу і угрупуванню залишилися 100 магазинів. Якщо в цьому випадку скористатися формулою Стерджеса, отримаємо:
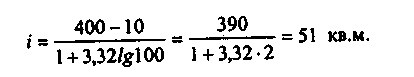
У цьому випадку сукупність рекомендується розбити на дев'ять інтервалів: у перших восьми інтервалах (відповідно до формули Стерджеса) буде розподілена основна маса магазинів (100), в останній інтервал увійдуть великі універмаги. Один з варіантів угруповання в цьому випадку може мати наступний вигляд:

У загальному випадку процес угруповання даних включає кілька етапів:
вибір группировочного ознаки;
упорядкування сукупності за цією ознакою;
визначення (тим чи іншим способом) кількості груп;
визначення меж інтервалів (зазвичай проводиться округлення формально отриманих даних).
Основне правило при проведенні угруповання полягає в наступному: не повинно бути порожніх або малозаполненних інтервалів. Іншими словами, формула Стерджеса дає лише орієнтовні значення інтервалів угрупування; при прийнятті остаточного рішення, як правило, значення округлюються або незначно змінюються.
В аналізі фінансово-господарської діяльності використовуються в основному два види угруповань: структурні і аналітичні.
Структурні угруповання призначені для вивчення структури і складу сукупності, що відбуваються в ній зрушень щодо обраного варьирующего ознаки. Структурна угруповання оформляється, як правило, у вигляді таблиці, в підметі якої знаходиться группіровочний ознака, а в присудок - показники, що характеризують структуру сукупності або в динаміці, або в просторі. Цей вид угруповання характеризує структуру сукупності по якомусь одному ознакою (у прикладі 2.11 такою ознакою є обсяг виручки торгових точок). Зміна структури угруповання найчастіше описується одним із двох показників.
Показник середнього абсолютного зміни структури розраховується за формулою:
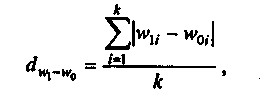

Показник среднеквадратического зміни структури розраховується за формулою:
Показник среднеквадратического зміни структури
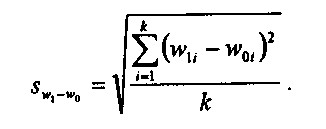
Чим більш значні структурні зрушення, тим більше значення цих показників. За відсутності структурних зрушень обидва вони рівні нулю. Квадратичний коефіцієнт реагує на зміну структури трохи більш чуйно. При розрахунку цих показників слід пам'ятати про те, що кількість груп в угрупованні і в базовому, і в звітному періодах має бути однаковим.
Аналітичні угруповання призначені для вивчення взаємозв'язків між двома і більше показниками, що характеризують досліджувану сукупність. Один з показників при цьому розглядається як результативний, а решта - як факторні. За аналітичної угрупованню можна розрахувати силу зв'язку між факторами.
При оформленні результатів угруповання в таблиці ознака-результат розміщується в присудок, групувальні ознаки, що розглядаються в якості факторних, розміщуються в підметі таблиці.
Вибрати один ознака в якості группировочного найчастіше буває досить важко. Аналіз за кількома ознаками досить трудомісткий і має принципову ваду - розмиванням сукупності, оскільки навіть комбінація двох ознак при спробі розбити сукупність на три або чотири категорії дає шість або вісім підгруп. У деяких з них виявляється одне-два спостереження, що недостатньо для підготовки обгрунтованих висновків про ці підгрупах. Уникнути цього недоліку дозволяють методи багатовимірних угруповань. Широке поширення вони одержали завдяки використанню обчислювальної техніки при розрахунках. При аналізі діяльності окремих підприємств методи багатовимірної угруповання використовують нечасто через їх складності, більш поширені вони при соціологічних та економічних дослідженнях галузей і регіонів. Найбільш розробленим методом багатовимірної класифікації є кластерний аналіз (див. розділ 2.8.3).
Інформація, релевантна " 2.7.2. Метод угруповання даних "
- 5. МЕТОДИ І ПРИЙОМИ АНАЛІЗУ ФІНАНСОВО ГОСПОДАРСЬКОЇ ДІЯЛЬНОСТІ
методів і прийомів. Для обробки економічної інформації користуються такими методами, як балансовий, базисний, графічний, і такими прийомами аналізу, як порівняння, угруповання, елімінування. Балансовий метод дає можливість встановити взаємозв'язок показників. В аналізі фінансово господарської діяльності використовуються різні балансові зіставлення і ув'язки. При базисному методі - Питання 4. Поняття угруповань, класифікацій і номенклатур в економічній статистиці. Єдина Система класифікації та кодування інформації
методами. Підставою для класифікації є ознака (критерій) або декілька ознак (критеріїв). Класифікатором в статистиці називається систематизований перелік об'єктів (галузей, підприємств і т. п.), кожному з яких присвоюється код. Код замінює назву об'єкта і служить засобом його ідентифікації. Номенклатурою в статистиці називається стандартний перелік об'єктів та їх - Метод бухгалтерського обліку
методом бухгалтерського обліку. Іншими словами, об'єктами бухгалтерського обліку, є кошти установи, джерела їх утворення та процес виконання робіт і послуг. Рис. 7.3.-Об'єкти бухгалтерського обліку Основними складовою методу бухгалтерського обліку є: документація, інвентаризація, оцінка, калькуляція, рахунки, подвійний запис, бухгалтерський баланс, звітність, - 5.1. Призначення бюджетної класифікації
методологічного підходу до складання і виконання всіх видів бюджетів, для порівнянності бюджетних показників у галузевому і територіальному розрізі. Бюджетна класифікація є обов'язковою для всіх установ і організацій та будується відповідно до вимог, визначених бюджетним законодавством Російської Федерації. У міру розвитку методів управління бюджетна класифікація - ОСНОВНІ ПОНЯТТЯ
методам розрахунків, які використовуються різними країнами, галузями і сферами господарства показників економічного розвитку з метою забезпечення їх - Ринковий підхід
методу оцінки: метод ринку капіталів, метод угод та метод галузевої оцінки. Метод ринку капіталів заснований на цінах продажу акцій подібних фірм на світових фондових ринках. Для застосування цього методу потрібно детальна фінансова і цінова інформація по представницької групі порівнянних фірм. Серцевина методу - фінансовий аналіз, вибір і обчислення оціночних коефіцієнтів (факторів). К - Методи історико-економічного аналізу
методів пізнання, застосовуваних цією наукою, пов'язана з використанням методологічного арсеналу, категоріального апарату, основних теоретичних побудов історичного та економічного знання і відображає їх взаємодія. Методи, що застосовуються при історико-економічних дослідженнях, поділяються на традиційні та новітні. У систему традиційних методів входять: 1) історичний - § 5. МЕТОДИ СКЛАДАННЯ МОБ
методом витрат, по рядках - по методу випуску. На другому етапі за методом витрат на основі як можна більш докладних даних про структуру проміжного споживання і компонентах валової доданої вартості визначають, яким чином всі витрати поділяються по окремих галузях (складається таблиця витрат). При цьому необхідно мати на увазі, що дані про види витрат є по «господарським» - § 1. ЗАГАЛЬНЕ ПОНЯТТЯ Про класифікації, групування та номенклатури І ЇХ РОЛЬ У статистичних досліджень
метод класифікації - це послідовний розподіл множини об'єктів на підлеглі класифікаційні угруповання. Спочатку безліч об'єктів підрозділяється по деякому обраною ознакою на великі групи, потім кожна з них - за іншою ознакою на ряд наступних угруповань, при цьому конкретизується об'єкт класифікації. Таким чином, між класифікаційними угрупованнями - Політико-економічний характер інтеграції
угруповання, і у відносинах з третіми країнами. Тому економічна інтеграція - це політико-економічний процес зі створення єдиного економічного простору країн, що входять в інтеграційне угруповання, з єдиним механізмом регулювання економічних і соціальних відносин між ними. Вона являє собою спосіб і форму розв'язання суперечності між національною економічною - Питання 45. Статистика інвестицій та інвестиційної діяльності
угруповання: 1) угруповання інвестицій по напрямки відтворення основних фондів; 2) угруповання інвестицій джерелами фінансування інвестицій; 3) угруповання інвестицій технологічним призначенням витрат; 4) угруповання інвестицій формами власності інвесторів та ін; При розподілі інвестицій в основний капітал за джерелами фінансування в цілому з економіки виділяють: - 5. РОСІЯ У МІЖНАРОДНІЙ СИСТЕМІ НАЦІОНАЛЬНИХ рахунків
методологічну раду Держкомстату Росії, за активної участі якого була розроблена спеціальна Державна програма на період 1992-2000 рр.. Основна мета цієї програми - створення умов для підвищення ефективності державного регулювання життя суспільства на основі об'єктивної та достовірної оцінки стану і можливостей різних форм власності, сфер економіки, - Питання +9. Основні угруповання населення. Показники демографічного навантаження населення. Розміщення населення по території країни
угрупованнями в демографічній статистиці є угруповання за статтю та віком. Населення за своїм складом за статтю ділиться на чоловіків і жінок, співвідношення між якими утворює статеву структуру суспільства. Статева структура суспільства характеризується за допомогою абсолютних і відносних показників. Серед абсолютних показників можна виділити показники чисельності чоловіків і жінок, - 2.8.3. Технологія планування
методів планування та можливостей технічних засобів їх розробки. Зазвичай виділяють наступні методи економічного планування: 1. Статистичний; 2. Нормативний; 3. Балансовий; 4. Експертний. СТАТИСТИЧНИЙ МЕТОД базується на статистичних даних, на підставі яких будують статистичні ряди, індекси, визначають темпи розвитку, екстраполіруемого на - Тема 7. Особливості прямого оподаткування в індустріальноразвітих країнах
метод обкладення корпоративних доходів, фіскальну значимість корпоративних податків, середній рівень податкових ставок, рівень справляння корпоративних податків і т.п. Далі необхідно розглянути, які системи оподаткування прибутку (доходів) корпорацій застосовуються на практиці, в чому їх схожість і відмінності, навести приклади країн, в яких застосовується класична система оподаткування прибутку