2.7.1. Метод середніх величин
Роль середніх величин, таким чином, полягає в узагальненні, тобто заміні безлічі індивідуальних значень ознаки середньої величиною, що характеризує всю сукупність явищ. Середня величина узагальнює якісно однорідні значення ознаки і, отже, є типової характеристикою ознаки в даній сукупності. Наприклад, середній товарообіг на одного працюючого є типової характеристикою торговельній мережі міста.
Зрозуміло, середня величина не фіксована раз і назавжди: середня вироблення на одного співробітника нормально функціонуючого підприємства постійно зростає. Середні витрати на одиницю продукції із зростанням обсягу випуску зазвичай падають. Таким чином, не тільки самі середні значення величин, а й тенденції їх зміни можна розглядати як індикатори положення підприємства на ринку і успішності його фінансово-господарської діяльності в даній галузі.
Існує кілька видів середніх величин. Найбільш простий і прозорий сенс має середня арифметична.
Середня арифметична величина - це таке середнє значення ознаки, при обчисленні якого загальний обсяг ознаки в сукупності не змінюється. Іншими словами, середня арифметична - це середнє доданок, при розрахунку якого загальний обсяг ознаки в сукупності розподіляється порівну між усіма одиницями. Наприклад, середня заробітна плата - це така величина заробітної плати, яка припадала б на одного працівника, якби весь фонд заробітної плати підприємства розподілявся між усіма співробітниками порівну. Формула для розрахунку середньої арифметичної:
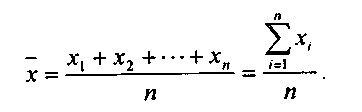
Так обчислюють середню величину, якщо відомі всі індивідуальні значення в сукупності. Якщо ж обсяг сукупності великий і представляє собою ряд розподілу, використовують значення середньозваженої арифметичної середньої. Формулу її розрахунку і використання в аналізі діяльності підприємства ілюструє приклад 2.5.
Приклад 2.5. Молокозавод випускає сметану різної жирності, реалізуючи її за різною ціною. Дані про реалізацію різних сортів сметани за тиждень представлені в таблиці.

Середня ціна за кілограм сметани повинна являти собою результат розподілу загальної виручки від продажу всіх сортів по всіх 1597 кілограмам реалізованої продукції. Обчислюється ця величина наступним чином:
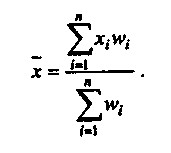
У нашому випадку розрахунок показує, що середньозважена середня арифметична ціна одного кілограма сметани, реалізованої молокозаводом за анализируемую тиждень, склала:
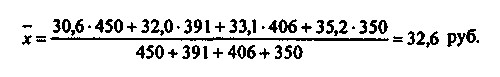
У середньої арифметичної величини є ряд властивостей, про які слід пам'ятати аналітику. Ці властивості такі.
По-перше, сума відхилень індивідуальних значень ознак від його середнього значення дорівнює нулю, тобто:
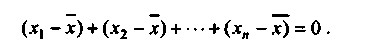
Дана властивість характерно і для середньозважених величин.
По-друге, якщо кожне індивідуальне значення ознаки помножити або розділити на якесь число, то і середня збільшиться або зменшиться в стільки ж разів, тобто:
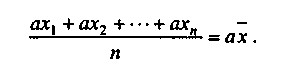
По-третє, якщо до кожного значення ознаки додати (або від нього відняти) яке число, то середня збільшиться (або зменшиться) на таке ж число, тобто:
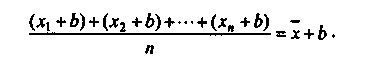
Це властивість іноді застосовують при оперуванні показниками з великими значеннями. Проілюструємо сказане на прикладі 2.6.
Приклад 2.6. Розрахувати середній квартальний обсяг реалізації продукції підприємством за даними за чотири квартали 1998

З кожного значення xi можна відняти 587 612, а потім розрахувати середню по "залишкам":

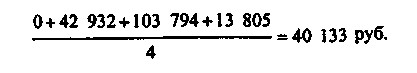
Шукана середня величина квартальної реалізації буде дорівнює
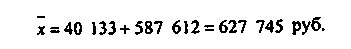
По-четверте, якщо ваги середньої зваженої помножити або розділити на одне і те ж число, величина середньої не зміниться, тобто:
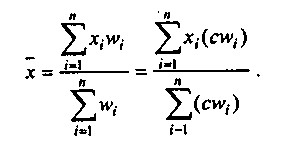
По-п'яте, сума квадратів відхилень індивідуальних значень ознаки від середньої арифметичної величини менше, ніж від будь-якого іншого числа. На цій властивості грунтується застосування методу найменших квадратів, який використовується для визначення виду регресійної залежності між факторами.
Крім середньої арифметичної використовуються і інші форми середніх величин. У першу чергу це середня геометрична, яка дозволяє зберігати незмінним не сума, а твір індивідуальних значень величини:
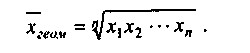
Основне застосування середня геометрична знаходить при вивченні темпів зростання. Розглянемо її використання на прикладі 2.7.
Приклад 2.7. Темпи зростання цін на сировину, що використовується у виробництві продукції підприємства, протягом чотирьох кварталів 1998 були різними. Потрібно знайти квартальний темп зростання цін в середньому за рік за даними за чотири квартали року.
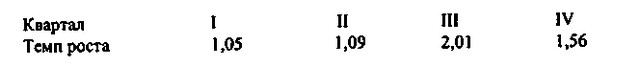
Темп зростання цін за рік склав: 1,05 - 1,09 - 2,01 - 1,56=3,59.
Якщо скористатися для розрахунку середнього темпу зростання формулою середньої арифметичної, отримаємо, що щорічний темп зростання склав в середньому 1,43 рази:
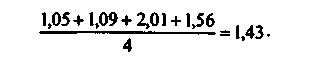
Отримане значення навряд чи дає достовірну картину темпів зростання, оскільки якщо припустити, що ціни кожен квартал збільшувалися в 1,43 рази, то тоді темп зростання за рік має скласти 4,15 рази:
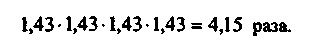
Для того щоб зазначене протиріччя не виникало, для розрахунку середнього квартального темпу зростання цін за рік слід використовувати формулу середньої геометричної:
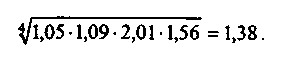
Середня геометрична дає найбільш правильний за змістом результат і в тих випадках, коли потрібно знайти таке значення економічної величини, яке було б якісно рівновіддаленим як від її максимального, так і від мінімального значення. Проілюструємо це на прикладі 2.8.
Приклад 2.8. В період найбільшої активності рентабельність діяльності готелю, розташованої на курорті, становить 60% на місяць, в періоди щорічного спаду (в так званий "мертвий" сезон) - 2%.
Розрахунок середньоарифметичної величини в даному випадку (припускаючи, що висока рентабельність має місце рівно половину року, а іншу половину - низька) дає результат:
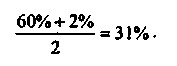
Така рентабельність - теж дуже високий показник. Це значення якісно ближче до 60%, тобто до максимуму, ніж до 2%, тобто до мінімуму. Такий фінансовий результат - свідчення високої рентабельності, він різко відрізняється від поняття "низька рентабельність". Тому для розрахунку величини, яка буде "якісно середньої" характеристикою рентабельності, слід використовувати формулу среднегеометрической:
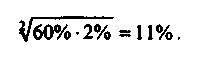
Ще один показник, що характеризує середні величини, - середня гармонійна. Він використовується у випадках, коли необхідно, щоб при усередненні залишалася незмінною сума величин, зворотних індивідуальним значенням ознаки. Формула розрахунку середньої гармонійної така:
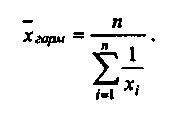
Використання середньої гармонійної величини ілюструє приклад 2.9.
Приклад 2.9. Робочий виготовляє на верстаті 520 деталей за денну зміну. У нічну зміну його вироблення становить 450 деталей. Яка середньозмінна виробіток на одного робітника, якщо денна та нічна зміни рівні за тривалості?
При розрахунку середньозмінної вироблення необхідно врахувати, що тривалість обох змін однакова і дорівнює t. Тоді:
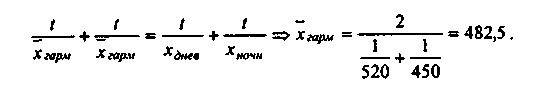
Між наведеними видами середніх величин існує наступне співвідношення:
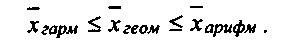
В аналізі фінансово-господарської діяльності широко використовується також середня хронологічна. Для характеристики підприємства застосовуються інтервальні і моментні показники. Прикладами перших є товарообіг, прибуток, обсяг надходження за деякий період; прикладами другого - дані про запаси, основні засоби, чисельності працюючих на певну дату. Для усереднення інтервальних показників найчастіше використовується формула середньої арифметичної, а для усереднення моментних показників як раз і застосовується формула середньої хронологічної.
Якщо дано ряд моментних показників: x1, ... , Хп, то середня хронологічна Sch, для цього ряду розраховується за формулою:
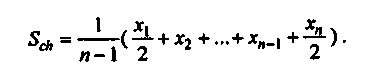
Приклад 2.10. Потрібно знайти величину середнього товарного запасу в магазині в 1999 р., якщо є такі дані про запаси на початок кожного кварталу (тис. крб.):
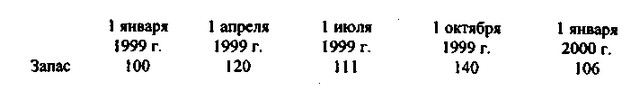
Користуючись формулою середньої хронологічної, знаходимо:
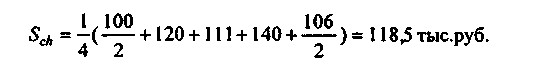
Економічна інтерпретація отриманої величини така: Протягом 1999 р. щодня підприємство мало запас товарів, рівний в середньому 118,5 тис. руб.
Підкреслимо, що отримане значення середньої хронологічної є умовним - воно дає уявлення про порядок, а не про точному значенні величини запасу, оскільки фактичний запас протягом аналізованого періоду може відчутно варіювати. Зокрема, якщо б у розпорядженні аналітика (у прикладі 2.10) були дані про запаси на початок кожного місяця або тижня, розраховане значення середнього запасу майже напевно було б іншим.
Інформація, релевантна " 2.7.1. Метод середніх величин "
- Співвідношення середньої та граничної продуктивності
середньої продуктивності певною мірою ідентичний характеру кривої граничної продуктивності. У той же час необхідно звернути увагу на наступні особливості співвідношення динаміки граничної і середньої продуктивності. По-перше, в тих випадках, коли гранична продуктивність перевищує величину середньої продуктивності, остання схильна зростанню. Середня - Взаємозв'язок середніх витрат
середніх загальних витрат можна сказати, що вони виступають як результату складання середніх змінних і середніх постійних витрат. Характер кривої середніх загальних витрат визначається положенням кривих середніх змінних і середніх постійних витрат. Мінімальна величина загальних середніх витрат досягається при більшому обсязі виробництва порівняно з його об'ємом, якому відповідає - Середнє падіння капіталу
метод характеризується співвідношенням два до одного між максимальним і середнім падінням капіталу. Якщо співвідношення має значення, менше цієї величини, то швидше за все максимальний спад буде більше. Інший коефіцієнт, який може дати деякі цінні відомості, - це співвідношення між середнім падінням капіталу і середньорічний прибутком. Тут використовується підхід, заснований на більш - Математичне сподівання
методу з іншими. У торгівлі я віддаю перевагу методи, які показують вище 0,6. Пам'ятайте: чим вище число, тим більш стійкими будуть результати. Чим менше число (нижче нуля), тим негативніше очікування. Для довідки: наступний вираз використовується для визначення математичного очікування: (1 + (середній виграш / середній збиток)) х відсоток виграшів - - ДВА ПОСЛІДОВНИХ ЗАКРИТТЯ НИЖЧЕ КОВЗНОЇ СЕРЕДНЬОЇ
метод вимагає, щоб крива реального поточного капіталу рухалася нижче ковзної середньої. Крім того, існує ще додаткова вимога: наступний рівень капіталу повинен бути нижче середнього, але в той же час дуже близько до нього. Таблиця 11.2. показує результати застосування цього методу на тому ж прикладі, який наводився раніше для ілюстрації методу ковзної середньої капіталу. - 14. МЕТОДИ РОЗРАХУНКУ ЦІН
методи ціноутворення. Витратні методи ціноутворення забезпечують розрахунок продажної ціни на товари та послуги за допомогою додавання до витрат або собівартості їх виробництва якоїсь конкретної величини. До ринкових методів ціноутворення відносяться: 1) метод поточної ціни; 2) метод «запечатаного конверту», або тендерного ціноутворення. До економічних методів ціноутворення відносять - Середня торгівля
метод або систему, яка дає менше 250 доларів у середній - 6.8. Інші способи застосування ковзних середніх
методів, конвергенція-дивергенція (MACD), користується зараз великою популярністю. Цей метод буде висвітлено в розділі про - АНАЛІЗ КОВЗНОЇ СЕРЕДНЬОЇ КАПІТАЛУ
методу ковзної середньої капіталу в торгівлі виникає питання щодо логіки цього методу. У попередньому прикладі наведені результати були дещо занижені для випадку торгівлі за допомогою ковзної середньої. У таблиці 11.1 дається розбивка за первісною серії з 132 угод з 9-денним середнім, а потім показується, які угоди були укладені і чому. Якщо навпроти угоди стоїть знак - 6.9. Поради щодо правильного застосування ковзних середніх. Переваги та недоліки методу
методів. Методи з використанням ковзних найкраще працюють в умовах тренда, хоча ніколи не сигналізують про стелю або дні ринку вчасно. Через це при бічному тренді запізнювання сигналів призведе до їх повної непотрібності. 103 Рис. 6.7. Способи горизонтального розташування однієї і тієї ж ковзної середньої Графік наданий агентством Dow Jones Telerate 104 - Специфіка кривої попиту
середній дохід (дохід, що припадає на одиницю продукції із загального обсягу її реалізації) дорівнює ринковій ціні. Таким чином, в результаті того, що ціна продукції дорівнює одночасно та середньому, і граничному доходу, на графіку крива попиту для окремо взятого підприємства одночасно представляє і ціну, і середній дохід, і граничний дохід. При безперервному нарощуванні ресурсів, що ведуть до