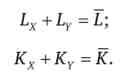
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Проаналізуємо тепер іншу сторону економіки - виробництво. Нехай в економіці виробляється два товари (X і Y). У виробничому процесі задіяно два види ресурсів - працю L і капітал К. Загальний обсяг трудових ресурсів становить L; загальний обсяг капітальних ресурсів дорівнює К. У виробництві товару X задіяно Lx праці та Дох капіталу. У виробництві товару Y зайнято Ly праці та Доу капіталу, так що
Розглянемо економіку конкурентних ринків. Ціни товарів і ціни ресурсів задані рівноважними станами відповідних ринків. Фірми не можуть вплинути на ціни, фірми є ценополучате- лями. Мета фірм полягає в максимізації прибутку при технологічному обмеження, заданому виробничою функцією. Мета споживачів - максимізація корисності від покупок товарних наборів. Виробничі функції та функції корисності представлені стандартними моделями.
Використовуємо для аналізу діаграму Еджуорт (рис. 21.7). По горизонтальній осі будемо відкладати обсяги застосованої праці, по вертикальній - обсяги капітальних ресурсів. Фактори виробництва для випуску товарах зображені в стандартному поданні: ізокванти зростають зліва направо. Фактори виробництва для випуску товару Y даються в перевернутому вигляді: ізокванти зростають справа наліво.
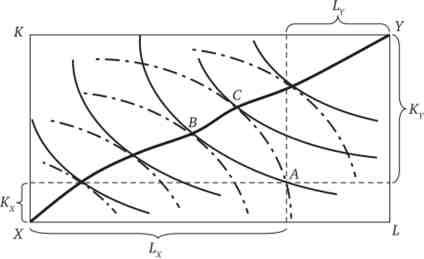
Мал. 21.7. Діаграма Еджуорт для загальної рівноваги у виробництві
Нехай первинний розподіл ресурсів в економіці представлено точкою А. У цій точці дві ізокванти двох виробничих процесів перетинаються. Чи є ця точка оптимальної з точки зору загальної рівноваги? Згідно з критерієм Парето точка А не є точкою ефективного розподілу виробничих ресурсів в економіці між випусками товарів X і У. Шляхом перерозподілу факторів виробництва, наприклад в точку В або точку С, можна збільшити сукупний випуск хоча б одного з товарів, не скорочуючи виробництво іншого виробу. Так як точки А і В розташовані на одній і тій же ізокванте для товара X, то перехід з точки А в ціль В збільшить випуск товару Y без зменшення виробництва товару X. Оскільки точки А і С розташовані на одній і тій же ізокванте для товара У, то перехід з точки А в точку З збільшить випуск товару X, не скорочуючи обсягу виробництва товару У. Перерозподіл ресурсів уздовж лінії ВС сприятиме зростанню випуску і одного, і іншого товару.
Як знайти точки В і С і аналогічні їм?
Візьмемо дві репрезентативні фірми, одна з який займається випуском тільки товару X, а інша виробляє тільки товар У. Кожна фірма прагне найняти ресурси в такому співвідношенні, щоб максимізувати свій прибуток. Так як мова йде про конкурентній економіці і фірми не можуть впливати на цінові параметри виробництва, то завдання максимізації прибутку зводиться до задачі максимізації випуску:
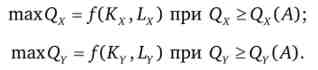
Вирішуючи цю задачу, отримуємо результат: MTRS *, = MTRSYKl. Ефективність загальної рівноваги у виробництві спостерігається там, де ізокванти відповідних випусків торкаються один одного, так що граничні норми технологічного заміщення ресурсів у виробництві різних товарів рівні між собою. Ці точки формують криву виробничих контрактів (Потовщена лінія ХУ на рис. 21.7). Крива виробничих контрактів показує альтернативні комбінації ресурсів і альтернативні комбінації товарів, які можуть бути зроблені при ефективному використанні факторів виробництва.
Оскільки загальний обсяг кожного ресурсу в економіці фіксований в кожен даний момент, то крива виробничих контрактів одночасно показує кордон виробничих можливостей цієї економіки. Висловивши криву виробничих контрактів у вигляді функції: Qx = F (QY), отримаємо криву виробничих можливостей (рис. 21.8), добре відому нам по гл. 2.
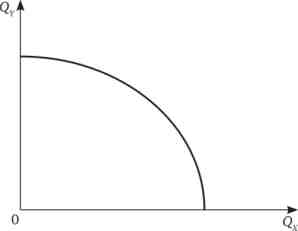
Мал. 21.8. Крива виробничих можливостей економіки
Тепер можна проаналізувати детально нахил КПВ. Нахил кривої виробничих можливостей показує граничну норму продуктової трансформації - пропорцію, в якій випуск одного товару (скажімо, товару X) може бути замінений виробництвом іншого товару (товару У) зі збереженням ефективності виробництва.
Гранична норма продуктової трансформації (Marginal rate of product transformation - MRPT) дорівнює
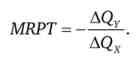
З іншого боку, крива виробничих можливостей може трактуватися як крива витрат суспільства на випуск двох товарів: С (Х; У). Ефективне виробництво вимагає повного використання наявних ресурсів, обсяг яких фіксований. Тому вздовж КВП повний диференціал функції витрат буде дорівнює нулю:
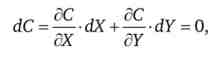
ДС
де - = МСХ - граничні витрати суспільства на випуск товару X;
мул.
ДС
- = MCY - граничні витрати суспільства на випуск товару Y; X і У - 8Y
обсяги виробництва двох товарів.
ЗЗО
Перегрупувавши складові, отримаємо ще один вислів для граничної норми продуктової трансформації:
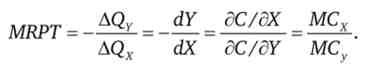
Таким чином, гранична норма продуктової трансформації оцінює відносні витрати випуску товарів, т. Е. Показує альтернативні витрати виробництва.
Завдання, що ілюструє концепцію
Нехай в економіці використовується один фактор виробництва - праця. Загальний обсяг трудових ресурсів становить 100 чел.-ч. Економіка може виробляти товар X і товар У відповідно до виробничих функціями: X
і У = ^ -
Чому дорівнює границя виробничих можливостей економіки?
Чому дорівнює гранична норма продуктової трансформації в цій економіці?
Рішення
Запишемо загальний обсяг праці в економіці: Lx+Ly = 100. Підставами в цей вислів значення ресурсів з відповідних виробничих функцій:
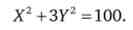
Це і є функція КПВ даної економіки. Її форма - еліпс при X > 0; У > 0. Знайдемо повний диференціал цієї функції
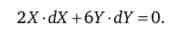
Звідки отримуємо граничну норму продуктової трансформації
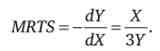 Таким чином, альтернативні витрати випускати складають ЗУ.
Таким чином, альтернативні витрати випускати складають ЗУ.
Використовуючи міркування, аналогічні ситуації, дослідженої в грошовій економіці обміну, можна довести, що в грошовій економіці виробництва рівноважні ціни ресурсів повинні бути такими, щоб:
MRTSu = MRTSykl = Лінія цін ресурсів в оптимумі стосуватиметься изоквант кожного виду виробництва. Якщо виробничі функції представлені опуклими изоквантой (наприклад, при стандартній моделі у вигляді функції Кобба - Дугласа), то така точка дотику буде єдиною для економіки з виробництвом.