| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Очевидно, що стан рівноваги на всіх ринках, крім ринку праці, в найпростішої неокласичної моделі визначається в тому числі і параметрами державної фіскальної та грошово-кредитної політики. Виникає природне запитання: як зміниться стану рівноваги при зміні параметрів макроекономічної політики? Відповісти на нього дозволяє порівняльна статика, в рамках якої порівнюються стану економіки «до» і «після» зміни якогось одного параметра - G, Т або М. Не можна з упевненістю відповісти на питання, що станеться, якщо змінити відразу кілька параметрів, - це вимагає знання конкретних функціональних залежностей усередині моделі. Крім того, як випливає з назви використовуваного методу, ми не аналізуємо динаміку переходу від одного стану рівноваги до іншого, а дивимося лише на самі стану рівноваги.
Розглянемо спочатку, что_проізойдет, якщо держава збільшить обсяг грошової маси з рівня до рівня М2. Як ми вже знаємо з аналізу передумов і структури моделі, зміна обсягу грошової маси ніяк не вплине на реальні показники, а тільки призведе до пропорційної зміни рівня цін і номінальної заробітної плати. На рис. 7.4 показані рівноважні рівні ціп Р * і Р2, відповідні Мх
и і р
і М2. Нескладно бачити, що -1- = - = ± -.
Ру М2
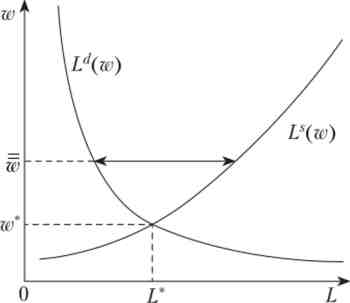
Мал. 7.3. Дефіцит попиту на ринку праці
Більш цікаві ефекти можуть надати зміни в обсязі державних закупівель та податків. Розглянемо спочатку зміна величини державних закупівель. Припустимо, що держзакупівлі збільшилися на «малу» величину dG. Відзначимо, що з формальної точки зору ми розглядаємо саме «мале» зміна обсягу державних закупівель. За відсутності точних знань про виробничу, інвестиційної функції і про функції споживання неможливо зробити загальні висновки поза сферою аналізу диференціального обчислення, що оперує малими величинами.
Перш за все слід зазначити, що рівноважна реальна зарплата, рівноважна зайнятість і рівноважний випуск не зміняться, так як вони визначаються виходячи зі стану ринку праці, на який величина держзакупівель впливу не робить. Крім того, не зміниться і розподіл реального наявного доходу на споживання і приватні заощадження (якщо функція споживання не залежить від реальної ставки відсотка). Відзначимо, що на ринок грошей зміна обсягу держзакупівель також не матиме ніякого впливу. Таким чином, зміни відбудуться тільки на двох ринках: продуктовому і фінансовому. Застосуємо теорему про неявну функцію до рівняння, що описує рівновагу на ринку продукту та фінансовому ринку. Розглянемо рівняння, що описує рівновагу на цих ринках, як визначення неявної функції:
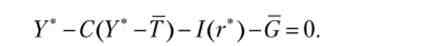
Повний диференціал цієї функції за умови, що державні закупівлі зросли на величину dG, задовольняє властивості:
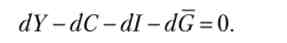
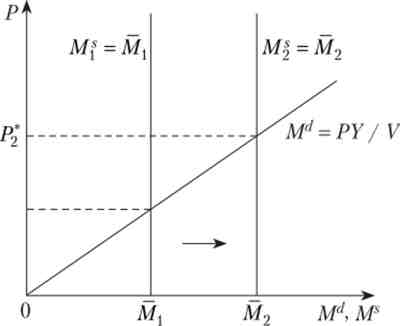
Мал. 7.4. Макроекономічна політика: збільшення грошової маси
Як ми вже встановили, dY = 0, dC = 0. Отже, dl = -dG. Враховуючи що dl = I'dr, отримаємо також, що
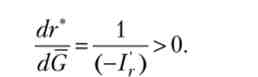
Таким чином, збільшення державних закупівель на величину dG призводить до зменшення інвестицій на ту ж величину внаслідок зростання реальної ставки відсотка. Це не повинно нас дивувати, оскільки фіксований пропозицію продукту ділиться між фіксованим приватним споживанням, держзакупівлями (які збільшилися в силу постанови держави) і інвестиціями, причому тільки останній компонент попиту може змінюватися, забезпечуючи рівновагу. Явище, коли через зростання державних закупівель зростає реальна ставка відсотка і знижуються приватні інвестиції, називається витісненням. При цьому мова йде про повне витіснення в тому сенсі, що приватні інвестиції зменшуються рівно на величину збільшення державних закупівель. Зауважимо також, що збільшення державних закупівель веде при незмінних податках до зростання первинного дефіциту державного бюджету, а значить, до збільшення державного боргу. Отже, збільшення попиту держави призводить до зниження приватних інвестицій і зростання державного боргу, т. Е. Не робить позитивного ефекту на економіку.
Розглянемо тепер зміна розміру стягуваних податкових зборів на малу величину dT. Слідуючи тій же логіці, отримаємо, що повний диференціал неявної функції задовольняє рівняння
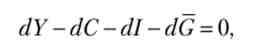
однак тепер незмінні загальний випуск і державні закупівлі. Приватне споживання та інвестиції змінюються:
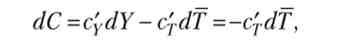
де Су - гранична схильність до споживання за доходом, a cf - гранична схильність до споживання по податках. В силу пристрою функції споживання, Су = з 'т. отже, c 'TdT = I'dr. Звідси отримуємо, що
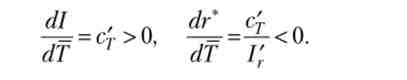
Таким чином, якщо, наприклад, зменшити податки, то особисте споживання збільшиться на деяку величину. На таку ж величину зменшиться обсяг приватних інвестицій, а рівноважна ставка відсотка зросте. Як і в разі зростання державних закупівель, не підкріпленого зростанням податків, зменшення податків без зменшення державних закупівель призведе до зростання первинного дефіциту державного бюджету і, отже, до збільшення державного боргу. Па рис. 7.5 показано, що рівноважна ставка при збільшенні державних закупівель або зниження податків збільшиться з г / до г2 при зменшенні заощаджень з до 5 * 2 Якщо це зменшення викликане збільшенням державних ^ закупівель з рівня G{ до G2j то зниження заощаджень складе S [-S2 ~ G2 -Gy Якщо ж це зменшення викликане зменшенням розмірів податків, що стягуються з величини 7j до Г2, то Si -S2 ~ З 'т(7j -Т2).
Таким чином, расширительная фіскальна політика (збільшення державних закупівель або зниження податків) призводить до зростання державного боргу і зниження інвестицій за рахунок зростання державного або приватного споживання. Тим самим підкріплюється тезу прихильників доктрини laissez-faire, які вважають втручання держави в економічні процеси шкідливим для економічного розвитку.
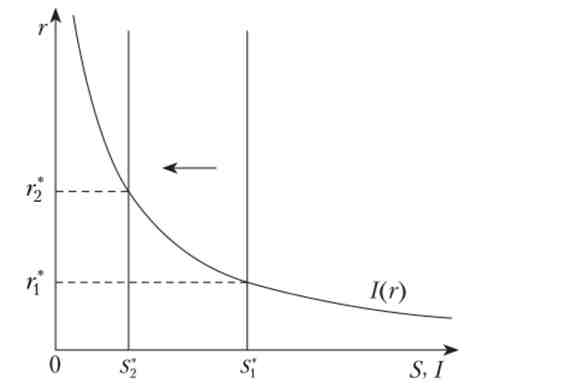
Мал. 7.5. Макроекономічна політика: зменшення пропозиції на фінансовому ринку
Стійкість. Коли говорять про економічну рівновагу, то явно або неявно мають на увазі рівновагу в сенсі дії деяких економічних сил. Якщо економічна система не знаходиться в стані рівноваги, то ці сили зрушують її в якомусь напрямку. Якщо ж в якомусь стані результуюча цих сил дорівнює нулю і не сприяє виходу економіки з цього стану, таку ситуацію називають станом рівноваги.
Одним з природних способів опису рушійних сил економіки є опис за допомогою системи диференціальних рівнянь. Відповідно, стан рівноваги моделюється економіки - це стан рівноваги в сенсі цієї системи, т. Е. Її нерухома точка. Очевидно, що дуже важливим є також питання про те, чи є стан рівноваги стійким або, ще краще, асимптотично стійким. Як відомо, нестійкі рівноваги «в реальному житті» не реалізуються. Слід зазначити, що один і той же стан може бути рівноважним в сенсі різних систем диференційних рівнянь, т. Е. Різного набору діючих економічних сил.
В рамках неокласичного підходу, коли говорять про стійкість, зазвичай мають на увазі стійкість так званого процесу намацування. Його можна описати приблизно так: якщо на ринку певного продукту, ресурсу або фактора попит вищий за пропозицію, то ціна цього продукту, ресурсу або фактора підвищується. І навпаки, якщо попит менше пропозиції, то ціна знижується. Наведемо цей процес за допомогою диференціальних рівнянь стосовно аналізованої моделі.
На ринку праці «ціною» є реальна заробітна плата w, тому ми можемо записати наступне диференціальне рівняння:
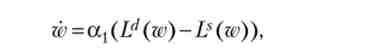
де оц > 0.
На фінансовому ринку «ціною» є ставка відсотка м Тим самим має сенс наступне диференціальне рівняння:
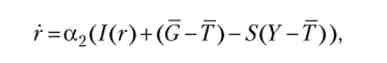
де а2 > 0.
Нагадаємо, що S (Y-T) = Y-Т -C (Y-Т). Щоб визначити величину К, скористаємося дією закону Сея і визначальною роллю ринку праці, поклавши Y = F (L), де L = Ld(W).
Тепер опишемо диференціальне рівняння, що стосується ціни Р. З одного боку, Р - це ціна на ринку товарів і послуг (ціна нашого умовного єдиного продукту), тому се зміни повинні залежати від попиту і пропозиції на цьому ринку. У той же час величина Р важлива для ринку грошей, так як ціною грошей можна вважати величину 1 / Р. У всякому разі, природно припустити, що якщо пропозиція грошей більше спроса_на них, т. Е. Якщо М > PY / V, то ринок грошей «штовхає» ціни вгору, а якщо М
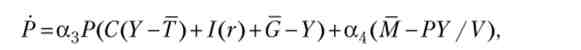
де а3 > 0, а4 > 0.
Система з трьох наведених вище диференційних рівнянь описує процес намацування стосовно аналізованої моделі. Слід зазначити, що при зроблених припущеннях щодо всіх вхідних в опис цієї системи функцій і досить великому безлічі початкових станів, у цієї системи рівнянь існує рішення.
Що ж стосується стійкості, то збіжність w {t) ^ w * при t -слід безпосередньо з Пропозиції А.1 (див. математичне додаток А). Ілюстрація збіжності на ринку праці наведена на рис. 7.6.
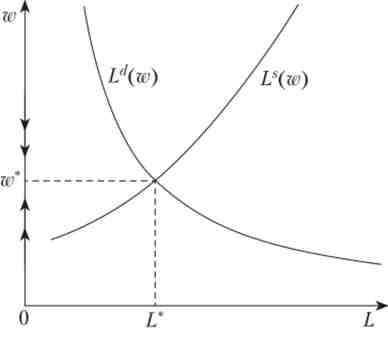
Мал. 7.6. Стійкість на ринку праці
При початковому умови w (0) = w * ми мали б рівність Y (t) = Y *. В цьому випадку збіжність г (?) - "г * теж витікала б з Пропозиції А.1, якого в загальному випадку для такої збіжності вже недостатньо. У той же час вона все ж має місце при досить слабких додаткових припущеннях. Це можна довести, модифікувавши і узагальнивши Пропозиція А.1.
Майже те ж саме вірно і з приводу збіжності P (t) -> Р У разі да (0) = w * і г (0) = г * вона просто випливає з Пропозиції А.1, але має місце і в загальному випадку. Суть полягає в тому, що з плином часу, в силу збіжності F (?) -> У *, динаміка г, описувана відповідним диференціальним рівнянням, стає практично такий же, як і динаміка, описувана рівнянням
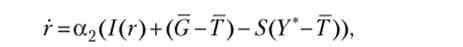
для якого Пропозиція А.1. вже діє. Відповідно, з плином часу динаміка Р, задається рівнянням
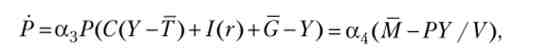
стає практично такий же, як і динаміка, обумовлена рівнянням
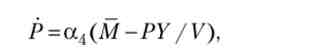
оскільки C (Y * - Т) + I (r *) + G-Y * = 0.
Відзначимо, що в наведених міркуваннях не ставилося умова, щоб початкові значення w {0), г (0) і Р (0) були близькі до рівноважних значень відповідних величин w *, г *, Р *. Іншими словами, мова йде про глобальну асимптотичної стійкості стану рівноваги в розглянутій моделі.