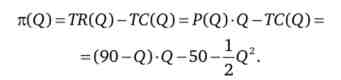Знайдемо умови першого порядку| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Фірма-монополіст може використовувати два типи цінової політики:
а) призначати єдину ціну на всі одиниці продукції, що продається; б) проводити стратегію цінової дискримінації, при якій різні обсяги і (або) різним споживачам продаються за різними цінами. У цьому параграфі мова піде про вибір оптимальної єдиної монопольної ціни. У параграфі 14.5 ми проаналізуємо механізм цінової дискримінації.
Розглянемо проблему максимізації прибутку для монополіста. Очевидно, що в умовах, коли крива попиту має негативний нахил, чим більша кількість товару монополіст хоче продати, тим нижче повинна бути ціна одиниці товару. Щоб сукупна виручка монополіста при цьому не зменшувалася, зниження ціни (і втрати монополіста на кожної додаткової одиниці товару, що продається) має компенсуватися значним збільшенням обсягу продажів. Отже, монополісту доцільно проводити операції в еластичною частини свого попиту.
Однак у міру збільшення випуску зростають витрати монополіста, так що кожна додаткова одиниця виробленої продукції обходиться йому дорожче (граничні витрати зростають). Тому монополіст буде розширювати випуск до тих пір, поки додаткова виручка від продажу додаткової одиниці товару перевищує або, принаймні, має величину не менше додаткових витрат, пов'язаних з її виробництвом, оскільки коли витрати виробництва додаткової одиниці випуску більше додаткової виручки, монополіст зазнає збитків .
Завдання, що ілюструє проблему
Фірма-монополіст стикається з лінійним попитом на свій товар: P (Q) = 90 - Q. Її сукупні витрати становлять: TC (Q) = 50 + ^ Q2. Який обсяг продажів
вибере фірма і яку вона призначить ціну, якщо компанія прагне максимізувати прибуток?
Рішення
Запишемо функцію прибутку компанії
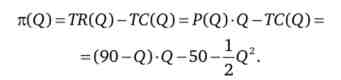Знайдемо умови першого порядку
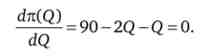
Звідки отримуємо обсяг продажів Q '= 30 і ціну Р = 60.
Однак чи принесе цей вибір фірмі максимальний прибуток? Для цього треба перевірити умова другого порядку
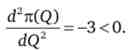
Ця умова максимізації прибутку виконується.
Крім того, слід переконатися в тому, що постійні витрати не поглинають весь прибуток:
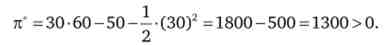
Таким чином, вибір Q"= 30 і Р'= 60 відповідає меті фірми - досягти максимального прибутку.
Проблема максимізації прибутку зводиться до знаходження максимуму функції прибутку tt (Q), який досягається там, де гранична виручка буде дорівнює граничним витратам: MR (Q) = MC (Q). Це буде так зване умова першого порядку функції прибутку: ^п^ = 0. Крім того,
dQ
необхідно переконатися, що дана точка є точкою максимуму, а не мінімуму прибутку. Це показує умова другого порядку, яке в простому випадку зводиться до знаходження другої похідної функції прибутку. Якщо друга похідна функції прибутку отрица- d2n (Q) п -
тельна: 2 < 0, знайдена критична точка відповідає точці максимуму прибутку. Однак самі по собі умови першого і другого порядків можуть гарантувати досягнення максимального прибутку тільки в довгостроковому періоді, коли всі витрати фірми є змінними і, отже, за визначенням, беруть участь у формуванні граничних витрат і прибутку.
У короткостроковому періоді присутні постійні витрати, які, хоча і впливають на загальну величину прибутку, що не мають прямого впливу на вибір оптимального обсягу виробництва, так як не впливають на величину граничних витрат. Тому в короткостроковому періоді може скластися така ситуація, коли фірма, вибравши за формальними критеріями обсяг виробництва, отримає нульову або навіть негативну прибуток, якщо її постійні витрати виявляться надмірно високими і перекриють одержувану без їх урахування прибуток. Ця ситуація ілюструється на рис. 14.2.
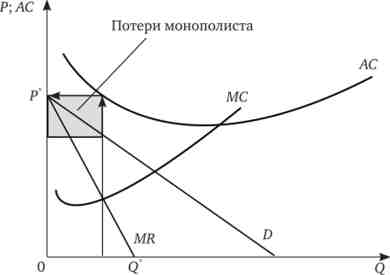
Мал. 14.2. Втрати монополіста в короткостроковому періоді
В такому випадку монополіст віддасть перевагу закрити провадження (QM = 0) і буде чекати зростання попиту або технологічних інновацій, які знижують витрати, а не виробляти «оптимальний» за формальними критеріями обсяг.
Ця проблема стає особливо актуальною у зв'язку з державним регулюванням монополіста. Найчастіше держава вводить паушальний (акордний) податок (наприклад, у вигляді плати за ліцензію або франшизу) на прибуток монополіста. Слід дуже акуратно підходити до такого заходу, оскільки надмірна величина подібного податку може призвести до закриття виробництва, що, поза всяким сумнівом, менш бажаний варіант, ніж навіть нерегульований монополіст.
Приклад, який ілюструє концепцію
Нехай функція попиту на продукцію монополіста має такий вигляд: p (Q) = а - bQ, а функція сукупних витрат представлена як: TC = F + cQ2 (де F - постійні витрати; с - коефіцієнт).
Знайдемо точку оптимального випуску монополіста з першого умови максимізації функції сукупного прибутку: MR = а - 2bQ = МС = 2cQ. Звідки
Q '= ---
2 (Ь + с)
Цей обсяг випуску може бути проданий за ціною
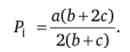
Знайдемо монопольний прибуток
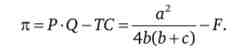
Тепер ми можемо написати функцію оптимального виробництва монополіста
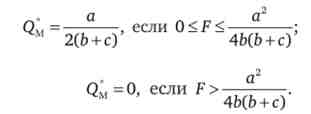
Нехай все ж фірма-монополіст стикається з подібною дилемою випуску. Як тоді монополіст встановить ціну?
Розглянемо докладніше граничну виручку фірми
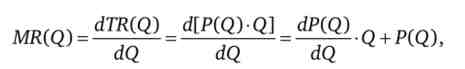
де P (Q) - функція попиту; -<0 - нахил функції попиту.
dQ
якщо Q > 0, монополіст випускає якийсь обсяг, то, як очевидно з цього виразу, функція граничної виручки завжди менше функції попиту:
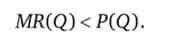
Значить, і в точці оптимуму, де MR = МС, функція граничної виручки і раніше менше функції попиту, менше ціни товару, яку готові платити споживачі. Тому ціна, яку призначає монополіст на свій товар, завжди буде вище граничних витрат його виробництва. А так як граничні витрати характеризують ціну вільної конкуренції, монопольна ціна виявляється явно вище ціни конкурентного ринку. Це і створює певні втрати добробуту для галузі.
З іншого боку, вираз - характеризує цінову еластичність попиту на товар фірми, в тому числі і фірми-монополіста. Тому
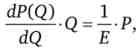
де Е - цінова еластичність попиту на товар фірми-монополіста.
тоді MR = P- ^ l + -J = МС. Звідки отримуємо вираз для величини монопольної ціни
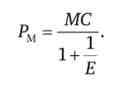
Оскільки цінова еластичність попиту - величина негативна і монополіст буде діяти в діапазоні еластичного попиту (| р | < 1), ми знову переконуємося в тому, що ціна монополіста виявляється вище граничних витрат виробництва товару.
Розглянемо тепер докладніше друга умова максимізації прибутку монополістом. Як ми знаємо, перша умова дає критичну точку, яка може виявитися і точкою максимуму, і точкою мінімуму функції прибутку. Для того щоб можна було говорити про максимум прибутку, має виконуватися друга умова
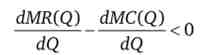
або
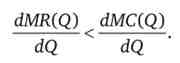
Функція граничної виручки завжди убуває, тому вираз в лівій частині завжди буде негативним. Якщо монополія діє в умови спадної, або, по крайней мере, незростаюча віддачі від масштабу (зростаючих або постійних граничних витрат), то права частина буде позитивною або рівною нулю - у всякому разі, буде завжди перевищувати вираз в лівій частині, що гарантує досягнення максимуму прибутку.
Складніше йде справа зі зростаючою віддачею від масштабу при відбувають граничних витратах. Якщо швидкість убування граничної виручки (реакція попиту) виявиться менше швидкості убування граничних витрат (реакції технології виробництва), то замість максимуму монополіст виявиться в точці мінімуму прибутку, але, як правило, це характерно для галузей природної монополії з дещо іншими параметрами поведінки і державного регулювання . Для тих монопольних ринків, з якими ми маємо справу в цьому розділі, така ситуація не зустрічається, хоча потенційну можливість цього треба все-таки мати на увазі.