8.2 Виробнича функція і функція витрат
Якщо, як було прийнято в главі 7, для виробництва продукції використовуються ресурси К і L, ціни яких г і w задані, то загальні витрати підприємства можуть бути представлені простим тотожністю:
С? RК + wL. (8.1)
Витрати, таким чином, залежать від цін використовуваних ресурсів і обсягу випуску, який у свою чергу залежить від кількості ресурсів До і L, необхідних для його отримання. Співвідношення між цінами ресурсів, їх кількостями, обсягом випуску і витратами можуть бути представлені за допомогою функції витрат. Функція витрат характеризує мінімальну суму витрат як функцію обсягу випуску і цін ресурсів.
Або, інакше, функція витрат характеризує загальний рівень витрат на виробництво певного обсягу продукції за умови, що підприємство використовує оптимальні комбінації ресурсів До і L. Останні визначаються, як було показано в попередньому розділі, киснем ізокванти, відповідної даному випуску, і ізокости. Тому (8.1) може бути в загальному випадку представлено як функція:
C (Q)=f [Q (K, L), r, w]. (8.2)
Вважаючи ціни ресурсів r і w незмінними, можна представити функцію витрат (8.2) графічно, як криву витрат. Ми будемо розрізняти витрати в тривалому періоді, або довгострокові витрати (LTC; long-run total cost - англ.), І витрати в короткому періоді, або короткострокові витрати (STC; short-run total cost - англ.). У тривалому періоді всі ресурси є змінними, в короткому - деякі з них постійні, кількість їх не може бути змінено в межах даного періоду. Крива довгострокових витрат може бути отримана на основі множин изоквант, що представляють деяку виробничу функцію, і ізокост, що характеризують певне співвідношення цін.
Найважливішим фактором, що визначає конфігурацію LTC, є характер віддачі від масштабу (рис. 8.1).
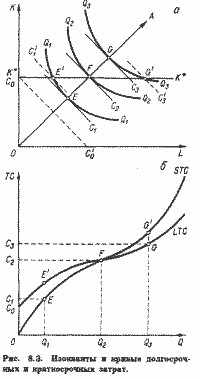
Оскільки в тривалому періоді немає постійних витрат, криві витрат при будь-якому характері віддачі від масштабу виходять з початку координат.
При постійній віддачі від масштабу крива LTC має вигляд прямої лінії або променя, що виходить з початку координат (рис. 8.1, б). Це означає, що загальні витрати збільшуються в тій же пропорції, в якій зростає обсяг виробництва. І це зрозуміло, оскільки випуск в цьому випадку зростає пропорційно збільшенню обсягу застосовуваних ресурсів, а ціни останніх не змінюються. При зростаючій віддачі зростання випуску випереджає зростання обсягів застосовуваних ресурсів. Це означає, що витрати на випуск 2Q * будуть трохи менше, ніж подвоєні витрати на випуск Q *. Тому крива LTC (рис. 8.1, г) опукла вгору, загальна сума витрат зі збільшенням випуску зростає, але зростає все повільніше. Нарешті, на рис. 8.1, е представлена крива LTC для випадку спадної віддачі від масштабу. Тут для подвоєння випуску потрібно більш ніж удвічі збільшити кількість застосовуваних ресурсів. Очевидно, що при незмінних цінах витрати будуть рости в більшій мірі, ніж випуск. Цьому відповідає опукла вниз конфігурація кривої LTC. Як зазначалося в розділі 7, у багатьох виробництвах зростаюча віддача від масштабу змінюється при досягненні певного обсягу випуску спадання. Виробничої функції з таким змінним характером віддачі від масштабу відповідає і змінюється конфігурація кривої довгострокових витрат. До певного рівня виробництва крива LTC опукла вгору, а поверх нього - вниз (рис. 8.
MC? ? TC /? Q, або МС? dTC / dQ. (8.3)
Це визначення застосовне для аналізу витрат і в тривалому, і в короткому періоді. Різниця ж між ними полягає в наступному. Довгострокові граничні витрати (LMC) характеризують приріст витрат при збільшенні випуску продукції на одиницю, якщо всі виробничі ресурси є змінними. Короткострокові граничні витрати (SMC; short-run marginal cost - англ.) Характеризують приріст витрат при збільшенні випуску продукції на одиницю, якщо частина застосовуваних ресурсів є змінною, а частина - постійною.
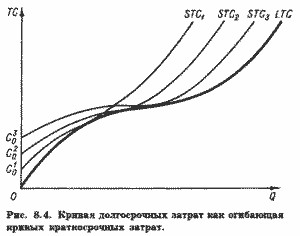
Графічно граничні витрати визначаються тангенсом кута нахилу дотичної до кривої загальних витрат у точці, відповідної тому чи іншому обсягом випуску.
Очевидно, що кут нахилу дотичної КК до кривої LTC в точці її перегину А (верхня частина рис. 8.2) менше кута нахилу дотичної в будь-який інший точці LTC.
Отже, мінімум LMC досягається при обсязі випуску Q1 (нижня частина рис. 8.2), якому відповідає точка А на кривій LTC. Аж до досягнення обсягу випуску Q1 граничні витрати зменшуються, а при подальшому збільшенні випуску зростають.
Середні, або, точніше (див. Додаток 8А), питомі (unit cost - англ.), Витрати визначаються як відношення загальних витрат до обсягу випуску:
ATC ? TC / Q. (8.4)
Довгострокові середні витрати (LATC) характеризують питомі витрати в розрахунку на одиницю продукції за умови, що всі виробничі ресурси є змінними. Короткострокові середні витрати (SATС) також характеризують питомі витрати в розрахунку на одиницю випуску, якщо частина використовуваних ресурсів є змінною, а частина - постійною.
Графічно середні витрати визначаються тангенсом нахилу променя, проведеного з початку координат до кривої загальних витрат у точці, що відповідає певному обсягу випуску.
Очевидно, що промінь ОВ (рис. 8.2) має нахил менше, ніж будь-який інший промінь, проведений з початку координат до якої-небудь іншій точці на кривій LTC. Це означає, що при обсязі випуску Q2 довгострокові середні витрати досягають мінімуму.
При обсязі випуску Q2 довгострокові середні витрати, очевидно, будуть рівні відношенню LTC до Q2. або LATC=BQ2/OQ2.
Як видно з рис. 8.2, при обсязі випуску Q2 довгострокові середні витрати виявляються рівні довгостроковим граничним витратам (LATC=LMC). У закономірності цього рівності легко переконатися, зауваживши, що промінь ОВ, нахил якого характеризує LATC, одночасно є і дотичної до кривої LTC в точці В, нахил якої характеризує LMC.
Таким чином, ми можемо сформулювати наступний важливий принцип: середні витрати досягають мінімуму при такому обсязі випуску, коли вони дорівнюють граничним. При цьому крива LMC перетинає криву LATC знизу вгору направо.
Ми можемо помітити також, що при меншому, ніж Q2, обсязі виробництва LATC> LMC.
У короткому періоді на відміну від тривалого підприємство не може змінити обсяг випуску за рахунок зміни кількості всіх виробничих ресурсів. Замість того щоб рухатися вздовж променя, що виходить з початку координат, воно змушене змінювати обсяг випуску, рухаючись вздовж лінії, паралельної осі змінного ресурсу (поверніться до рис.
Тому крива короткострокових витрат не збігається з кривою довгострокових витрат. Зокрема, вона проходить вище кривої LTC всюди, крім точки взаємного торкання.
Звернемося до рис. 8.3, а, де представлено сімейство изоквант Q1Q1-Q3Q3-Якби підприємство могло варіювати обсяги ресурсів До і L, їх оптимальні комбінації розташовувалися б уздовж лінії росту, представленої променем, що виходить з початку координат.
Відповідна крива LTC показана на рис. 8.3,6.
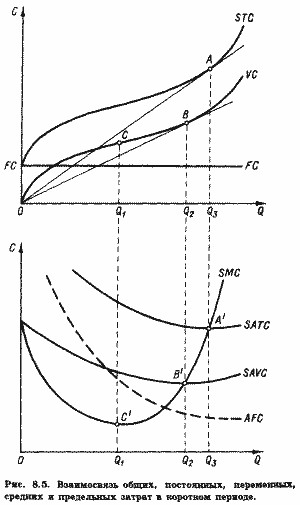
Нехай підприємство знаходиться в точці F на лінії росту (рис. 8.3, а), випускаючи Qi одиниць продукції при витратах Q2. Якщо підприємство має намір скоротити випуск до Q1, воно не зможе зробити це, рухаючись вздовж лінії росту в точку Е і відповідно знижуючи суму витрат до C1. У короткому періоді йому доведеться рухатися вздовж лінії постійного ресурсу К * К * до точки Е '. Оскільки точка E не є точкою дотику ізокванти Q1Q1 і ізокости, вона представляє більш високий рівень витрат, ніж точка Е. Це виявляється з того, що изокоста, що проходить через Е ', лежить вище ізокости, що проходить через Є.
Значить, загальні витрати в точці Е 'вище, ніж C1 (рис. 8.3,6). А звідси випливає, що в короткому періоді при випуску, меншому Q2, STC> LTC. Навіть у тому випадку, якщо підприємство припинить виробництво (скоротить випуск до нуля), йому не вдасться зменшити кількість постійного ресурсу і, значить, доведеться нести певні витрати. Такі витрати зазвичай і називають постійними. У прикладі, наведеному на рис. 8.3,6, постійні витрати рівні C0.
Припустимо тепер, що підприємство має намір збільшити випуск до Q3. Однак у короткому періоді точка G для нього недосяжна, бо кількість постійного ресурсу обмежена К *. Тому для досягнення обсягу випуску Q3 підприємству доведеться перейти в положення G''. І в цьому положенні, як і в положенні Е ', короткострокові витрати виявляться вище довгострокових - STC> LTC.
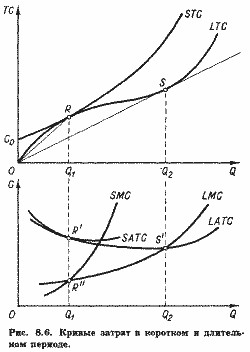
І лише при випуску Q2 довгострокові і короткострокові витрати рівні, STC (Q2)=LTC (Q2). Це випливає з того, що при випуску Q2 звичайна лінія росту перетинається лінією постійного ресурсу, паралельної осі змінного ресурсу (точка F на рис. 8.3, а). Тільки при такому випуску фіксована кількість ресурсу До виявляється оптимальним. При будь-якому іншому випуску крива STC виявиться вище кривої LTC, оскільки неможливість змінити кількість постійного ресурсу не дозволяє досягти в короткому періоді того мінімуму витрат, який можливий в умовах тривалого періоду. Відмінності в кількостях постійного ресурсу, природно, призводять і до різних кривим короткострокових витрат. Збільшення обсягу постійного чинника можна представити як зрушення лінії К * К * на рис. 8.3, a вгору. При цьому лінія К * К * перетинатиме промінь ОА вище і правіше точки F, тобто при все більшому обсязі випуску. Нова крива короткострокових витрат буде в результаті стосуватися кривої LTC також при все більшому випуску. Дійсно, криві STC1-STC3 на рис. 8.4 представляють криві короткострокових витрат при різних обсягах постійного ресурсу. Таким чином, ми можемо уявити криву довгострокових витрат LTC як огибающую для нескінченно великого числа кривих STC.
Інформація, релевантна " 8.2 Виробнича функція і функція витрат "
- 9.2.5. ПРОПОЗИЦІЯ АБСОЛЮТНО КОНКУРЕНТНІЙ ГАЛУЗІ В короткий період
виробничих витрат підприємств. Воно полягає у припущенні, що витрати на виробництво якого-небудь підприємства є функцією лише його обсягу виробництва, але не залежать від випуску інших фірм або галузі в цілому. Це припущення справедливо для виробництв (галузей), що не використовують високоспеціалізованих ресурсів (включаючи працю), та / або відносно невеликих порівняно з усією - Виробнича функція
виробничого процесу (производственнойтехнологии) часто описується як інженерно-тех-технічне рішення, за яким слід економіч-ське рішення Інженер або інший технічний ек-спертий відбирає технологічні процеси, характе-різующіеся мінімальними потребами в ресу-рсах, відкидаючи всі ті, які є техноло-гически неефективними . Потім настає очередьбізнесмена приймати - 3. Функції ринку
функцій (рис. 5.1). Рис. 5.1. Функції - 2. Виробництво в краткосрочномперіоде
виробничою функцією, ха-теризується залежність обсягу випуску від обсягу змінних витрат фірми при неизмен-них витратах інших факторів. Для простоти рас-дивимося приклад, в якому праця є едина змінним фактором виробництва В табл. 8-2 показана залежність між випу-ському глобусів фірмою «Джайгентік Глоуб Компа-ні» і чисельністю працівників, зайнятих у виробництві - Зважаючи повсемест-ве впровадження комп'ютерної техніки та пов'язані з цим переваги і зручності нового способу життя,
виробничої функції. Якщо ми позначимо обсяг своєї продукції як Y, кількість праці - L, кількість фізичного капіталу - К, кількість людського капіталу - H і кількість природних ресурсів - N, виробнича функ-ція виразиться таким чином: Y=AF (L, K, H, N), TReFi) - функція, що визначає залежність обсягів випуску продукції від значень витрат факторів - § 2.4. Функції оподаткування
функції оподаткування як прояви його сутності і властивостей, то в першу чергу необхідно відзначити, що в податках безпосередньо реалізується їхнє соціальне призначення як інструмента вартісного розподілу і перерозподілу доходів государства1. У той же час необхідно відзначити, що на практичному рівні оподатковування виконує кілька функцій, у кожній з яких реалізується те - Опції ринку праці
виробничий ресурс. Відповідно до цього виділяють головні функції ринку праці. Соціальна функція полягає у забезпеченні нормального рівня доходів і добробуту людей, нормального рівня відтворення продуктивних здібностей працівників. Економічна функція ринку праці полягає в раціональному залученні, розміщенні, регулювання та використанні праці, що дозволяє особливо - Опції ринку праці
виробничий ресурс. Відповідно до цього виділяють головні функції ринку праці. Соціальна функція полягає у забезпеченні нормального рівня доходів і добробуту людей, нормального рівня відтворення продуктивних здібностей працівників. Економічна функція ринку праці полягає в раціональному залученні, розміщенні, регулювання та використанні праці, що дозволяє особливо - 2. Основні функції сучасної держави
функції, які принципово не може здійснити сам ринок. Це насамперед такі функції: 1) регулювання так званих зовнішніх (або побічних) ефектів; 2) задоволення потреб у колективних благах (або в громадських - 2. Основні функції сучасної держави
функції, які принципово не може здійснити сам ринок. Це насамперед такі функції: 1) регулювання так званих зовнішніх (або побічних) ефектів; 2) задоволення потреб у колективних благах (або в громадських - Ключові терміни
Функція споживання Гранична схильність до споживання (MPC) Гранична схильність до заощаджень (MPS) Функція інвестицій Сукупний попит Функція сукупного попиту Небажане або незаплановане інвестування в запаси Мультиплікатор Парадокс - 6.3. Моделі економічного зростання
виробничої функції, показує взаємодію і взаємозамінність праці і капіталу: наскільки продукт зобов'язаний своїм створенням тому чи іншому чиннику, при якій їх комбінації може бути досягнутий максимум продукції при найменших витратах. Вона виражається рівнянням Q=f (K, L), (6.2) де Q - обсяг виробництва; f - функція; К - розмір капіталу; L - витрати праці (у вартісному