| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Для оцінки оптимізації введемо такі позначення: г-- очікувана прибутковість i-й цінного паперу; i = 1,2, ..., т, ni - частка i-й цінного паперу в портфелі; - коваріація між i-й і j-й цінними паперами; гр - очікувана прибутковість портфеля; прор - стандартне відхилення очікуваної прибутковості портфеля.
Відповідно до теорії ймовірності
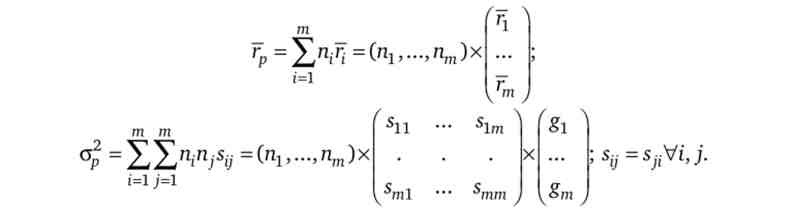
Дана функція корисності інвестора, що характеризує його ставлення до прибутковості і ризику: U = ррр-прор, де | / - параметр переваги між ризиком і прибутковістю.
Завдання. угр-зр -> Тах при = 1.
Рішення. Скористаємося функцією Лагранжа
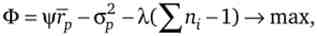
де X - співмножник Лагранжа.
Умови максимізації в матричної формі мають такий вигляд:
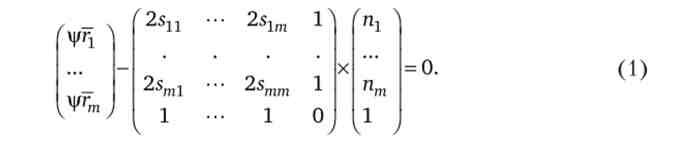
Позначимо буквою R зменшуване в рівність (1), перший співмножник від'ємника (матрицю) - літерою С, а другий співмножник (вектор) - буквою G. Тоді умова максимізації функції Лагранжа можна записати у вигляді
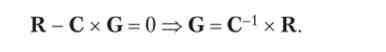
Визначимо зворотну матрицю до матриці С. Для стислості позначимо всі її елементи, крім останнього стовпчика і останнього рядка, а-. Елементи останнього стовпця і останнього рядка виходять однаковими, і їх позначимо с-.
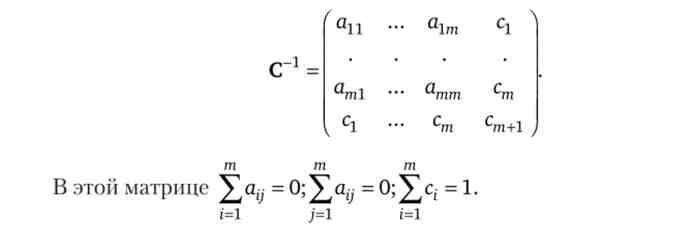
Для визначення оптимальної структури портфеля залишається вирішити систему рівнянь
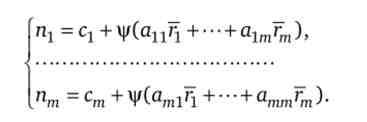
т
позначивши bt = Отримаємо наступну формулу для розрахунку
; = 1
оптимальної частки кожного виду цінних паперів в портфелі:

Визначимо портфель з мінімальним ризиком. Параметр / являє собою тангенс кута, утвореного віссю ординат і дотичній до області вибору інвестора в точці, що відповідає оптимальному портфелю (див. Рис. 5.8). Коли інвестор віддає перевагу портфелю з мінімальним ризиком, тоді дотична стає паралельної осі ординат, тому f = 0. Отже, у такого портфеля n = cv т. е. останній рядок (рядок) зворотної матриці С-1 представляє структуру портфеля з мінімальним ризиком. Прибутковість і ризик його будуть
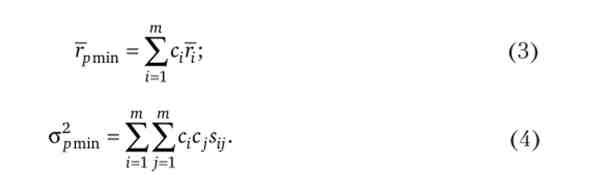
Для визначення структури портфеля, що відповідає іншим вимогам інвестора, зручно використовувати специфічний показник
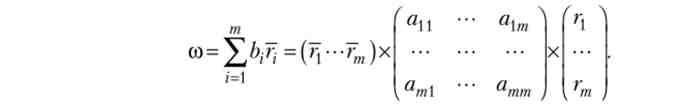
За допомогою показників rpm [n, a/; Min і зі легко можна знайти структуру портфеля, відповідного конкретним вимогам інвестора.
Припустимо, потрібно сформувати портфель із заданою очікуваною прибутковістю 7р. Відповідно до равенствами (2) і (3)
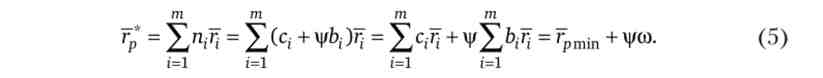
З рівності (5) визначимо, яким значенням у відповідає бажання інвестора мати очікувану прибутковість портфеля, що дорівнює гр,

Підставивши значення у, отримане з виразу (6), в рівняння (2), знайдемо структуру портфеля із заданою очікуваною прибутковістю.
Для визначення структури портфеля із заданим ступенем ризику візьмемо до уваги, що
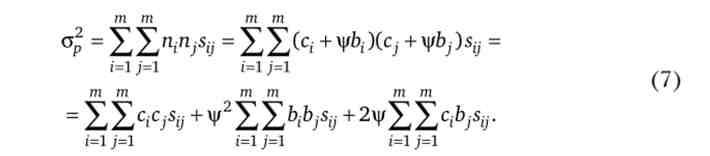
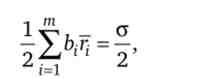
Перший доданок у виразі (7) - варіація портфеля з мінімальним ризиком (див. Рівність (4)). Після перетворень другий доданок можна представити у вигляді
а третій доданок дорівнює нулю. Тому
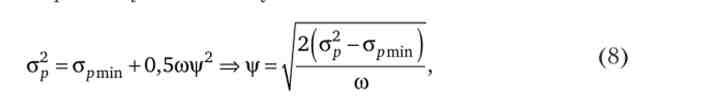
Підставивши вираз (8) в рівняння (2), знайдемо структуру портфеля із заданим ступенем ризику.
приклад
На основі спостережень за фондовим ринком для трьох видів акцій встановлені характеристики, представлені в табл. 1.
Таблиця 1
|
акція |
п,% |
а(, % |
Кореляція р-. |
Коваріація s-. |
||||
|
А |
В |
З |
А |
В |
З |
|||
|
А |
10 |
14 |
1 |
0,5 |
- 0,35 |
196 |
98 |
-196 |
|
В |
15 |
14 |
- |
1 |
0,3 |
196 |
168 |
|
|
З |
25 |
40 |
- |
- |
1 |
1600 |
||
Складемо з цих акцій портфель: а) з мінімальним ризиком; б) максимізує функцію корисності U = 40гр-з2р; в) з очікуваною прибутковістю 17%; г) з ризиком Gp = 18%. В даному прикладі матрицю системи рівнянь (1) можна представити у вигляді табл. 2, а зворотний до неї - у вигляді табл. 3.
Таблиця 2
|
А |
В |
З |
||
|
А |
392 |
196 |
-392 |
1 |
|
В |
196 |
392 |
336 |
1 |
|
З |
-392 |
336 |
3200 |
1 |
|
1 |
1 |
1 |
0 |
Таблиця 3
|
0,00339 |
-0,004 |
0,00062 |
0,69882 |
|
-0,0040 |
0,00508 |
-0,00107 |
0,15469 |
|
0,00062 |
-0,0010 |
0,00045 |
0,1465 |
|
0,69882 |
0,15469 |
0,1465 |
-246,83 |
Останній стовпець в табл. 3 вказує на те, що в портфелі з мінімальним ризиком повинно бути акцій,%: А - 69,88, В - 15,47 і С - 14,65. Звернемо увагу на те, що акцій А в портфелі виявилося значно більше, ніж В, хоча по поєднанню прибутковості та ризику перші поступаються другим. Очікувана прибутковість такого портфеля дорівнює 12,97% при а;= 11,11%.
Для визначення структури портфеля, максимізує задану функцію корисності, обчислимо Ь ;.
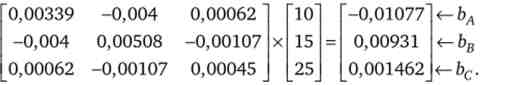
Тепер за формулою (2) знайдемо шукану структуру портфеля:
 Очікувана прибутковість цього портфеля гр = 15,7%, а прор = 13,35%.
Очікувана прибутковість цього портфеля гр = 15,7%, а прор = 13,35%.
За формулою (6) визначимо значення | /, відповідне бажанням інвестора мати г = 17%,
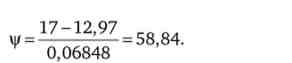
І знову за формулою (2) знайдемо шукану структуру портфеля:

Портфель з такою структурою має гр = 17%, ар= 15,55%.
І нарешті, визначимо структуру портфеля з ризиком стр = 18%. Такому бажанням інвестора відповідає

тоді
Такий портфель має rp = 18,21%, прор = 18%.