| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Вибір в умовах невизначеності і ризику можна проаналізувати, використовуючи інструментарій теорії поведінки споживача в умовах визначеності. Завдання індивіда полягає в тому, щоб максимізувати очікувану корисність при виборі оптимального варіанта з бюджетного безлічі. Так як ситуація невизначеності і ризику оцінює ймовірності різних результатів, введемо поняття обумовленого (контингентного) блага (Contingent commodity). обумовлене благо - це грошовий дохід або запас фізичних товарів, одержуваних індивідом в разі реалізації одного з безлічі можливих результатів. Доступ індивіда до цього блага залежить від настання даного результату з певною ймовірністю. Функція очікуваної корисності описує переваги індивіда щодо різних наборів обумовлених благ.
Припустимо, що в майбутньому можливо два стану для індивіда: сприятлива і несприятлива ситуація. Сприятлива ситуація супроводжується великим доходом (хороший урожай, зростання попиту на товар, що поставляється індивідом, відсутність стихійних лих, пожеж, повеней, крадіжок). Несприятлива ситуація тягне за собою втрати доходу (майна). Нехай ймовірність успішного результату оцінюється якр. Тоді ймовірність несприятливого результату складе (1 - р).
Якщо функція корисності індивіда визначена як U (I) (де I - дохід (вартість майна) індивіда), то функція очікуваної корисності (функція корисності від контингентних благ) буде дорівнює: EU (I) = = р? Іог) + (1 - р) - U (I2) (Де /, > /2).
Точки, що відповідають наборам обумовлених благ з однаковим рівнем очікуваної корисності, складають, як і в разі вибору споживача в умовах визначеності, криві байдужості. Для індивіда, не схильну до ризику, в силу угнутості функції корисності криві байдужості будуть опуклі до початку координат (рис. 10.4, а). Для індивіда, схильного до ризику, криві байдужості представлені увігнутими лініями (рис. 10.4, б). Для індивіда, нейтрального до ризику, криві байдужості приймають вид прямих ліній (рис. 10.4, в).
Що можна вважати лінією бюджетного обмеження для споживача в світі контингентних благ?
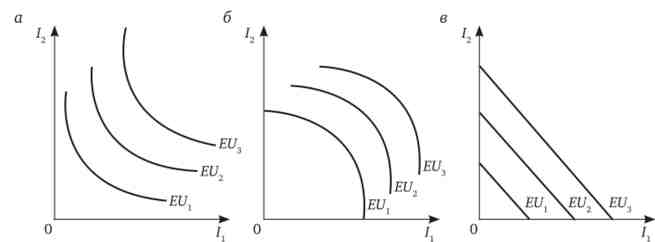
Мал. 10.4. Криві байдужості для різних типів індивідів
Якби дохід споживача був однаковий при будь-якому результаті, то ми отримали б лінію, що виходить з початку координат під кутом 45 °. Цю лінію можна охарактеризувати як «лінію впевненості», оскільки вздовж неї індивід має грошовою сумою напевно (зі 100% -ою впевненістю). В даному випадку ризик відсутній.
Кожна точка лінії впевненості відповідає якомусь безризикового грошовому еквіваленту, такому, що
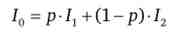
або
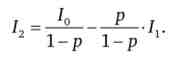
Цю лінію можна назвати лінією очікуваного доходу, або лінією справедливих шансів (Fair odds line). Вона грунтується на інтуїтивному уявленні про те, що у справедливій грі ціна ризикового результату повинна бути дорівнює відповідної ймовірності. В даному випадку ціна успішного результату - це значення ймовірності р; ціна несприятливого результату - значення ймовірності (1 - р).
Раціональний індивід не братиме участі в несправедливою грі. Тому дана лінія виявляється лінією бюджетного обмеження індивіда в умовах невизначеності і ризику.
Тепер ми можемо сформулювати завдання оптимального вибору обумовлених благ:
Max EU (I) при 10 = Р? f + (1 - р) - 12.
Для індивіда, не схильну до ризику, з умови першого порядку слід
Нахил функції очікуваної корисності має дорівнювати нахилу бюджетного обмеження (лінії справедливих шансів).
Звідки отримуємо: MUi = MU1 => Lj +12. Оптимум індивіда, не схильну до ризику, розташований на лінії впевненості (рис. 10.5).
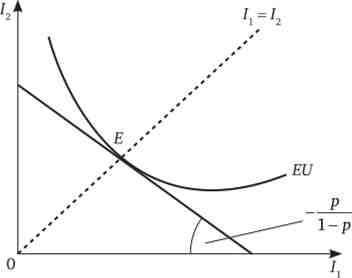
Мал. 10.5. Оптимум індивіда, не схильну до ризику
Завдання, що ілюструє теорію
Фермер згідно багаторічними спостереженнями вважає, що існує 50% -ва ймовірність того, що наступний сезон буде надзвичайно дощовим.
Його функція корисності дорівнює: С / (У1, У2) = - ^ 1пУ| +^ 1пУ2 (гДе У, - дохід фермера в нормальний рік; У2 - дохід фермера в дощовий рік). Фермер вибирає між двома зерновими культурами, прибутковість яких представлена в таблиці:
|
зернова культура |
Г, |
До |
|
Пшениця |
28 000 |
10 000 |
|
Кукурудза |
19 000 |
15 000 |
Рішення
1. Знайдемо очікувану корисність фермера при вирощуванні пшениці
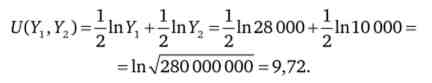Знайдемо очікувану корисність фермера при вирощуванні кукурудзи
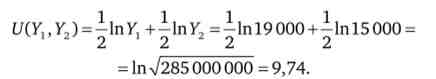
Корисність фермера при вирощуванні кукурудзи більше, отже, вирощування їм цієї культури краще, ніж пшениці.
2. Якщо фермер буде засівати тільки половину полів наявних культур, то це буде означати, що прибутковість кукурудзи і пшениці впаде вдвічі, т. Е. Очікувана корисність в даному випадку складе
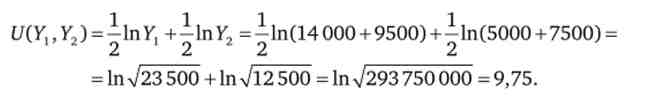
Таким чином, очікувана корисність фермера в даному випадку більше, ніж в разі засівання всього поля. Отже, фермер вважатиме за краще цю стратегію.
Порівняємо корисності і очікуваний дохід.
- У разі засеіванія пшеницею всього поля корисність буде дорівнює
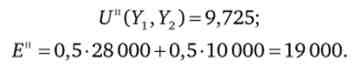
- У разі засеіванія кукурудзою всього поля корисність буде дорівнює
- У разі засеіванія половини поля кожної культурою корисність (Um) буде дорівнює
В результаті
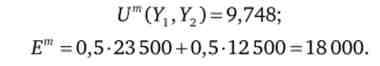
Порівнюючи корисності і очікуваний дохід, можна сказати, що якщо фермер людина раціональна і максимізує свою корисність, то він, швидше за все, засіє половину полів пшеницею, а решту полів кукурудзою. Якщо ж він прагне отримати більший дохід і схильний до ризику, то він, швидше за все, вибере варіант з великим можливим доходом, т. Е. Засіє поле пшеницею, при цьому ризикуючи в разі дощового року мати менший дохід. Якщо фермер прагне отримати максимальний очікуваний дохід, то він засіє поля тільки кукурудзою.
3. Нехай фермер засіває частина поля пшеницею, іншу частину - кукурудзою. Нехай а - частка поля, засіяного пшеницею, тоді (1 - а) - частка поля, засіяного кукурудзою.
Запишемо дохід фермера в вдалий рік:
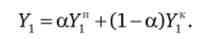
Дохід фермера в невдалий рік
Тоді очікувана корисність фермера дорівнюватиме
Очевидно, потрібно знайти
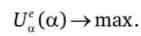
Умова першого порядку складе
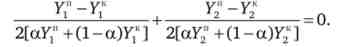Звідки отримуємо оптимальне значення
Очікувана корисність фермера в цьому випадку дорівнює
Таким чином, максимальна очікувана корисність фермера буде при засеі-
4 "5" _
вання - частини поля пшеницею і - всього поля кукурудзою. При цьому співвідношенням
9 9 4 9
ня вирощуваних культур складе: - - = 4: 5.