| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Тепер у нас є весь необхідний інструментарій для знаходження оптимального набору споживача. Ми знаємо, що споживач максимізує корисність товарного набору при бюджетному обмеженні. Розглянемо формальну сторону питання.
Умови виведення оптимального вибору споживача:
Питання пошуку оптимуму зводиться до математичної задачі максимізації цільової функції при наявності обмеження. Це завдання вирішується за допомогою функції Лагранжа.
Історична довідка
Жозеф Луї Лагранж (1736-1813), французький математик італійського походження. Народився в Турині (Італія). Закінчив Туринський університет, потім викладав математику в Королівській артилерійській школі в Туріні (в той час Сардинское королівство). У 1766-1787 рр. працював в Берліні на запрошення прусського короля Фрідріха І. У 1756 р був обраний іноземним членом Берлінської академії наук. З 1787 року і до кінця життя працював в Парижі, де викладав курс математичного аналізу в Еколь Нормаль, потім в Політехнічній школі. У 1772 р був обраний членом Паризької академії наук. Вважається поряд з Ейлером кращим математиком XVIII ст. Наполеон подарував Лагранжу титул графа, посада сенатора і орден Почесного легіону. За заслуги перед наукою він удостоївся честі бути похованим в Пантеоні. Головні досягнення пов'язані з узагальненням і синтезом накопиченого наукового матеріалу в області механіки і варіаційного числення.
Використовуючи цю функцію, оптимальний вибір споживача можна записати в наступному вигляді:
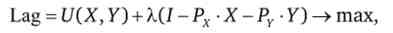
де X - множник Лагранжа.
Знайдемо умови першого порядку для даної функції. У функції Лагранжа, записаної вище, три змінні: X, Y і X.
Умови першого порядку дорівнюють
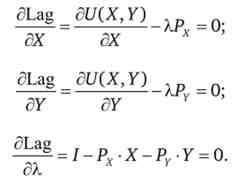
Розділивши перше рівняння на друге, отримаємо зручний вираз для пошуку оптимуму
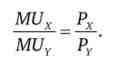
Вираз зліва - відношення граничних корисностей двох товарів - характеризує граничну норму заміщення в споживанні (MRSC). Вираз справа - ставлення цін товарів - показує ринкову норму обміну, або граничну норму заміщення в обміні (MRSE). Таким чином, в оптимумі споживач вибирає такі обсяги товарів, при яких його суб'єктивна норма заміщення MRSC була б дорівнює нормі обміну, що склалася на ринку (MRSE).
Перегрупувавши елементи цього виразу, отримаємо ще одну характеристику оптимуму споживача
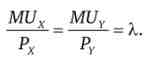
Ставлення граничних корисностей товарів до їх ринковими цінами в оптимумі виявляється однаковим для всіх товарів, які купує споживач. І дорівнює це відношення множнику Лагранжа (А,), який характеризує тут граничну корисність доходу, або грошей, споживача. Дане правило носить назву «Еквімаржінал'ний принцип поведінки споживача». Суть цього принципу полягає в тому, що в точці оптимуму додаткова грошова одиниця (додатковий дохід споживача) приносить споживачеві однакову корисність, незалежно від того, на який товар вона витрачається.
Якщо еквімаржінальний принцип порушується, наприклад МЧХ. >
PY Р
то індивіду вигідно змінити обсяги споживання товарів: збільшити купівлю товару, який приносить велику користь в розрахунку на одну грошову одиницю, і скоротити придбання товару, який приносить меншу корисність в розрахунку на одну грошову одиницю. В даному прикладі індивіду слід збільшити споживання товару Y, а товари скоротити. Тоді зі зростанням обсягу споживання товару Y його гранична корисність знизиться, а зі зменшенням споживання товару X його гранична корисність збільшиться (відповідно до закону спадної граничної корисності) аж до відновлення принципу рівності граничних корисностей в розрахунку на одну грошову одиницю (згідно еквімаржі- нальному принципом).
Оптимум споживача можна зобразити графічно (рис. 6.10). Лінія бюджетного обмеження показує максимально допустимі набори. Криві байдужості характеризують цінність товарів в очах споживача. Так як залишати невитрачені гроші споживачеві недоцільно, оптимум обов'язково буде знаходитися на лінії бюджетного обмеження. Нам залишається знайти таку криву байдужості, яка максимально віддалена від початку координат (лінія з найвищою корисністю) і яка все ще допускається бюджетом. У цьому випадку лінія бюджетного обмеження виявиться дотичній до даної кривої байдужості. точка дотику Е і є шукана точка оптимуму.
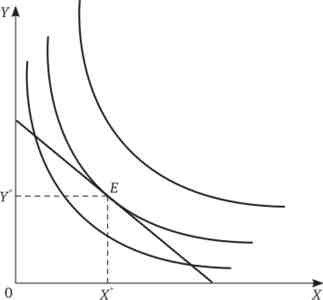
Мал. 6.10. оптимум споживача
продуктовий набір (X *; У) - це оптимальний вибір споживача в даних умовах.
Питання для роздумів
Чи є оптимум споживача єдиним? Які умови необхідні, щоб вибір споживача був єдиним? Коли оптимальних наборів може бути кілька?