Модель Самуельсона - Хікса

Модель Самуельсона - Хікса включає в себе тільки ринок благ, і тому рівень цін і ставка відсотка передбачаються незмінними; обсяг пропозиції благ абсолютно еластичний.

Обсяг споживання домашніх господарств в поточному періоді залежить від величини їхнього доходу в попередньому періоді

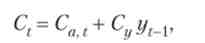
де З_{а t} - автономне споживання в поточному періоді.

Підприємці здійснюють автономні інвестиції (1_а г), Обсяг яких при заданій ставці відсотка фіксований, і індуковані інвестиції (I_{jn г}), залежать від приросту сукупного попиту в попередньому періоді і величини акселератора (ц):

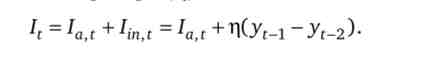
На ринку благ встановиться динамічна рівновага, якщо 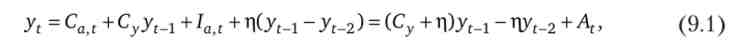де А₍ = C_at + I_{(L t}.

Рівняння (9.1) є неоднорідним кінцево-різницевим рівнянням другого порядку, що характеризує динаміку національного доходу в часі.

При фіксованій величині автономних витрат (A_r = А = Const) в економіці досягається динамічна рівновага, коли обсяг національного доходу стабілізується на певному рівні у, т. Е. y_t ⁼ Ус-1 = Уг-2 ⁼ - ⁼ Уг-п ⁼ У ^гЛ^{е п} ~ ^число періодів з незмінною величиною автономних витрат.

З рівняння (9.1) випливає, що у = А / ( 1 - З_{/ у}).

Подивимося, яка буде динаміка національного доходу, якщо в стані динамічної рівноваги зміниться величина автономного попиту.

Звільнимося від неоднорідності в рівнянні (9.1). значення y_t і у задовольняють рівності (9.1), тому можна записати наступне однорідне кінцево-різницеве рівняння другого ступеня з постійними коефіцієнтами:

де Ay_t= y_t-y._

Так як y_t= Y + Ay_t, то напрямок зміни y_t визначається напрямом зміни Ду_г

З теорії розв'язання диференціальних і звичайно-різницевих рівнянь слід, що характер зміни Дy_t залежить від значення дискриминанта характеристичного рівняння. Оскільки в даному випадку дискримінант дорівнює (C_v +т |)² -4л, то динаміка національного доходу залежить від граничної схильності до споживання, що визначає величину мультиплікатора і акселератора.

якщо {Із_у + л)² -4л > 0, то зміна y_t відбувається монотонно; при {Із_у + л)² -4л < 0 воно буде коливальним. Отже, графік функції З_у = - л + 27л, зображений на рис. 9.3, відокремлює безліч сполучень З _у л, що забезпечують монотонне зміна у_р від безлічі комбінацій з значень З_у, л, що призводять до коливань у_г

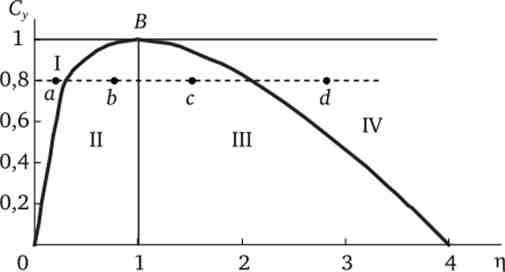
Мал. 9.3. області поєднань З_у, л

Спрямовується Чи має значення y_t до деякої кінцевої величиною або йде в нескінченність, залежить від значення останнього доданка характеристичного рівняння. якщо r 1, то рівновага встановиться на певному рівні. при г порушену рівновагу більше не відновиться. Коли Л = 1, тоді величина y_t буде коливатися з постійною амплітудою.

В результаті все безліч поєднань З і л виявилося розділеним на п'ять областей, як це показано на рис. 9.4. якщо значення З_у і л вказують на область I, то після порушення рівноваги в результаті зміни автономного попиту значення y_t монотонно кинеться до нового рівноважного рівня у₁ = А₁/ (1 С_у). при значеннях З_у і л, що знаходяться в області II, національний дохід досягне нового рівноважного рівня, пройшовши через затухаючі коливання. поєднання значень З_у і г, розташовані праворуч від перпендикуляра, опущеного з точки В на вісь абсцис, відповідають нестабільного рівноваги. Коли поєднання значень З_у} л вказують на область III, тоді динаміка y_t набуває характеру вибухових коливань. комбінації значень С, л ^в області IV призводять до того, що після порушення рівноваги y_t монотонно спрямовується в нескінченність. І нарешті, якщо акселератор дорівнює одиниці (п'ята область), то при будь-якому значенні граничної схильності до споживання у разі порушення рівноваги виникають рівномірні незгасаючі коливання у_г

приклад 9.1

Задані функція споживання домашніх господарств: C_f = 50 + 0,8y_f і функція попиту підприємців на автономні і індуковані інвестиції: I_t = 250 + г | (У {-1 ~ У 1-2) ' Протягом деякого часу до періоду t₀ включно економіка знаходиться в динамічній рівновазі при попиті підприємців на автономні інвестиції в обсязі 250 ден. од. Це означає, що в кожному періоді проводилося 1500 од. благ, з яких 50 + 0,8 - 1500 = 1250 споживають домогосподарства. З періоду t_{ підприємці вирішили, що обсяг автономних інвестицій має дорівнювати 350 ден. од. Як в результаті реалізації цього рішення буде змінюватися величина сукупного попиту (отже, і національного доходу) при чотирьох різних поєднаннях С, rj, представлених на рис. 9Л точками а, / ;, з і d, показано в табл. 9.2-9.5.

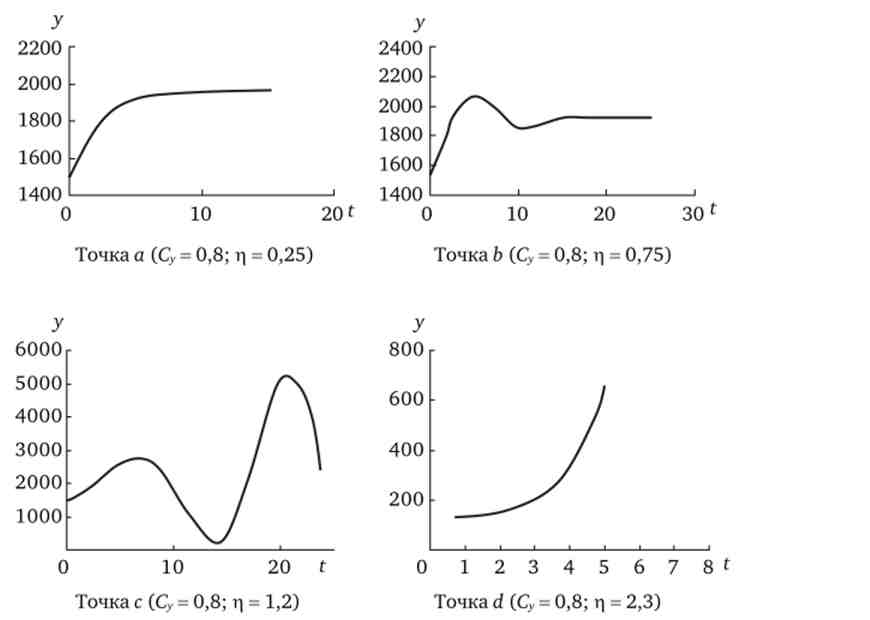
Мал. 9.4. Динаміка національного доходу після зміни автономного попиту при різних поєднаннях З_у, г |

Таблиця 9.2. Динаміка національного доходу при С = 0,8; Г | = 0,25

Таблиця 9.3. Динаміка національного доходу при З_у = 0,8; п = 0,75

ТАбліцов 9.5. Динаміка національного доходу при З_у = 0,8; п = 2,3

У моделі динаміка національного доходу в випадках, коли поєднання З_у, д відповідають областям III і IV (cm. Рис. 9.3), представляється неправдоподібною: не може в короткому періоді обсяг виробництва багаторазово зрости або знизиться. Це протиріччя пояснюється тим, що в моделі не були враховані дві обставини. По-перше, вироблений національний дохід не може істотно перевищити національний дохід повної зайнятості; цим обмежується амплітуда коливань обсягу національного доходу зверху. По-друге, як зазначалося в підпункті 3.1.2, обсяг негативних індукованих інвестицій не може перевищити суму амортизації; це обмежує амплітуду коливання національного доходу знизу. В результаті, коли поєднання З_у, г | відповідають областям III і IV, модель взаємодії мультиплікатора і акселератора набирає вигляду

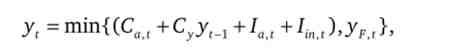
гаї hn. t = ^max {-Д Л (г /, _ 1 - У, _ ₂)}. якщо У, У_Р, ^і h ,,. з = У< ~^Ct ~ К, i ^ПР^І Ус * У г З урахуванням цих обставин приріст автономних інвестицій призводить до коливань національного доходу навіть при знаходженні поєднання С, г | в області IV.

Приклад 9.1 (продовження!)

Додамо до умов прикладу 9.1 обмеження: y_F= 3000 і D = 500. Тоді при значеннях З_у = 0,8 і г | = 2,3 після збільшення автономних інвестицій на 100 ден. од. величина національного доходу не спрямовується в нескінченність, як представлено на рис. 9.4, а коливається в інтервалі {158; 3000} (рис. 9.5 і табл. 9.6).

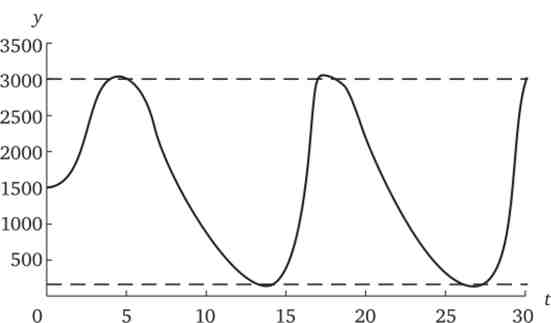
Мал. 9.5. Межі амплітуди коливання національного доходу

Таблиця 9.6. Взаємодія мультиплікатора і акселератора при З_у = 0,8, Г | = 2,3, = 3000, D = 500

Включимо в модель взаємодії мультиплікатора і акселератора ще один фактор - зростання населення. Нехай в результаті зростання населення автономний попит щорічно збільшується в (1 + п) раз. Тоді рівняння (9.1) приймає вигляд

де А₀ - автономний попит в нульовому періоді.

У цьому випадку внаслідок мультиплікативного ефекту величина рівноважного національного доходу щорічно буде зростати в (1 + п) раз:

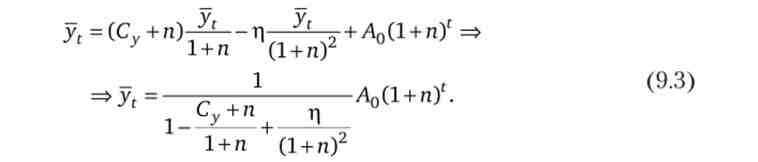
Перший співмножник в правій частині виразу (9.3) називають супермультіплікатор Хікса. Він показує, наскільки збільшується сукупний попит на рік U якщо на додаток до щорічного зростання автономного попиту, обумовленого зростанням населення, на одиницю зростуть автономні інвестиції.

Внаслідок щорічного збільшення населення з тим же темпом зростатимуть автономні витрати і національний дохід повної зайнятості - верхня межа можливих коливань національного доходу

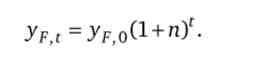
Екзогенний зростання автономного попиту підвищує і нижню межу коливань національного доходу, навіть якщо допустити зростання амортизаційних відрахувань з тим же темпом, що і автономний попит

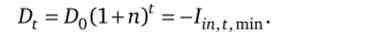
Тоді в ситуаціях, які відповідають областям III і IV, після збільшення автономного попиту з темпом (1 + п) коливання національного доходу будуть відбуватися в похилому коридорі.

Нехай в періоді t₀ встановилася рівновага при З = 0,75у, 1_а = 200; у = 800; ц = 2,2; D = =] () (); (//, = 1500. З періоду t, автономні інвестиції і амортизаційний фонд зростають з темпом 1,03. Коливання національного доходу в цих умовах представлені в табл. 9.7 і на рис. 9.6.

Таблиця 9.7. Взаємодія мультиплікатора і акселератора при постійному зростанні автономних витрат і фонду амортизації

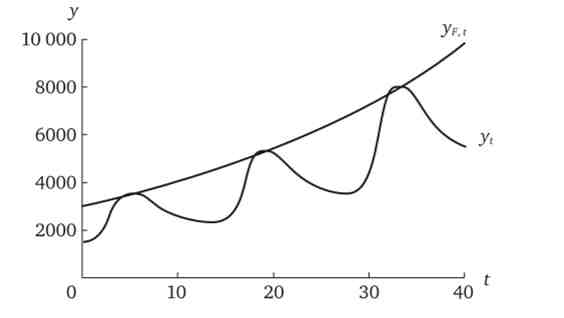
Мал. 9.6. Динаміка національного доходу при поєднаннях З_у, д в областях III і IV у разі постійного зростання автономних витрат і амортизаційних відрахувань

1. Найпростіші моделі сукупної пропозиції, кейнсіанські моделі сукупної пропозиції
   У попередньому параграфі ми вивели функцію сукупного попиту, що показує залежність загального попиту з боку всіх економічних агентів (репрезентативного споживача, репрезентативного виробника, держави) в залежності від рівня цін. В цьому і наступному параграфах ми розглянемо функцію сукупної
2. Найпростіша модель зростання народонаселення
   Економічна теорія пов'язує будь-демографічні зміни перш за все з ресурсними і виробничо-технологічними змінами, а зростання населення з результатами розвитку економічних відносин і зростання продуктивності праці. Основне положення теорії народонаселення було сформульовано ще в XVIII ст. англійським
3. Національний рахунок операцій з капіталом, національний фінансовий рахунок, національний баланс активів і пасивів
   Метою рахунку операцій з капіталом є відображення інвестицій в нефінансові активи і засобів, які можна використовувати для їх фінансування. Джерелами коштів є: а) валове заощадження (внутрішнє джерело); б) чисті капітальні трансферти (отримані мінус виплачені), які є зовнішніми джерелами коштів
4. Національні моделі в системі link
   Більшість національних моделей в системі LINK можуть бути віднесені до числа традиційних макроекономічних моделей відкритої економіки. Хоча господарська діяльність визначається в основному попитом, в деякі моделі введені обмеження з боку пропозиції. Попит на виробничі фактори і ціни було зроблено
5. Народногосподарський кругообіг і національне рахівництво, народногосподарський кругообіг
   Найважливіші макроекономічні показники обчислюють за допомогою системи національних рахунків (економічній бухгалтерії). У свою чергу національне рахівництво грунтується на моделі народногосподарського кругообігу, в якій процес функціонування національної економіки зображується у вигляді замкнутих
6. Моніторинг і прогнозування, що здійснюються з високою частотністю
   Побудова моделей послідовних періодів прогнозування для забезпечення введення початкових умов для динамічних систем, розрахованих на більш тривалий час, є надійною дослідницької стратегією. В інформаційний вік цю процедуру застосовують при розробці складаються з високою частотністю систем
7. Монетарна концепція економічних циклів
   Незважаючи на те що в моделі Тевеса присутній ринок грошей, в ній, як і в моделі Самуельсона - Хікса, причиною кон'юнктурних циклів виступають екзогенні зміни попиту на блага. Монетарні концепції економічних циклів пов'язують коливання економічної кон'юнктури з ендогенними змінами
8. Модель зростання Калдора
   У моделі Домара норма заощадження однакова для всіх суб'єктів, тут вона більше у підприємців (s { ), Ніж у робітників (s 2 ): s { > s 2 . Заощадження підприємців складають частку s { від доходу на капітал ГК, т. е. вони рівні s { rK, де г - ставка відсотка. Заощадження робітників складають