| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Припустимо для простоти викладу, що в економіці є всього дві галузі: шахта і електростанція.
Кожна галузь виробляє один продукт, який споживається домогосподарствами, але також служить ресурсом при виробництві даного і іншого продукту. Шахта виробляє вугілля, який використовується не тільки на електростанції, а й на самій шахті, наприклад для роботи електрогенераторів. Електростанція виробляє електроенергію, яку частково використовує сама, а інший обсяг поставляє на шахту і домогосподарствам. Таким чином, в моделі кожен ресурс є одночасно продуктом, і навпаки. Оскільки галузь виробляє один продукт, ми часто замість «галузі» говоримо про «продукт», і навпаки.
Прямі витрати - витрати одного ресурсу (продукту) при виробництві одиниці іншого продукту (ресурсу). Нехай - витрата г-го продукту при виробництві одиниці у-го продукту, тоді А = {АА є матриця прямих витрат. Її діагональні елементи менше одиниці: ап - его витрати вугілля при виробництві 1 т вугілля, т. е. частина видобутого вугілля витрачається на шахті. випуск i-й галузі Q, назвемо валовим випуском, а попит споживачів на її продукт Д - товарним випуском. Валовий випуск більше товарного.
Міжгалузевий баланс - стан економіки, в якому задовольняється споживчий і виробничий попит на кожен продукт і при цьому не проводиться їх надлишків. Передбачається лінійна залежність випуску продукту від витрат ресурсів, т. Е. Постійний ефект від масштабу виробництва у всіх галузях. Тому модель міжгалузевого балансу називають лінійної балансової моделлю, або моделлю Леонтьєва.
Проміжний попит - витрата продукту в якості виробничого ресурсу. Складемо рівняння балансу для кожної галузі. Витрата вугілля на шахті дорівнює auQh на електростанції - al2Q,2? Валовий випуск вугілля за вирахуванням виробничих витрат, або проміжного попиту, дорівнює товарному випуску:
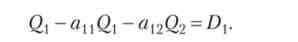
Аналогічно для другої галузі:
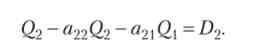
Ми отримали систему двох лінійних рівнянь щодо валових випусків, вона пов'язує технологічні параметри, випуски і обсяги попиту в збалансованій економіці. Запишемо її в матричному вигляді:
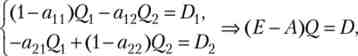
де Е - одинична матриця; Q і D - вектори валових і товарних випусків.
При заданих прямих витратах і обсягах попиту система має єдине рішення, за винятком випадків, коли матриця (Е - А) незворотна або один з валових випусків виявляється негативним. В обох випадках збалансованого стану не існує.
Повні витрати - приріст валового випуску одного продукту при збільшенні товарного попиту на інший продукт на одиницю. Розглянемо матрицю С, зворотний до матриці (Е - А), тоді
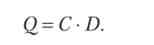
З'ясуємо зміст матриці З = {Су}9 для цього висловимо приріст валового випуску / -й галузі через прирости товарних випусків:
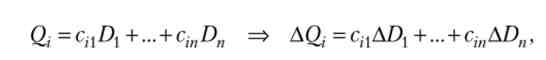
де п - число галузей.
Нехай попит па j-й продукт змінився на AZ);, а на решту продуктів залишився незмінним, тоді для збереження балансу валовий випуск i-й галузі повинен змінитися на Звідси зхх дорівнює приросту валового випуску / -го продукту при збільшенні на одиницю споживчого попиту на j-й продукт:
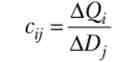
Отже, матриця З - це матриця повних витрат. якщо Су = 0, то зміна попиту на j- й продукт не зажадає зміни випуску / -го продукту. Чим більше тим сильніше впливає зміна товарного випуска7-го продукту на валовий випуск / -й галузі.
Нехай змінюється попит на продукт даної галузі, т. Е. / = j. Якщо споживчий попит на вугілля збільшився на 1 т, то буде потрібно збільшити виробничі витрати вугілля на шахті на ап, а для цього потрібно збільшити виробництво електроенергії і т. д. В результаті валовий випуск вугілля збільшиться більш ніж на 1 + аі. Отже, деяке збільшення споживчого попиту на продукт викликає збільшення його валового випуску на велику величину, т. Е. Діагональні елементи матриці повних витрат більше одиниці. В цілому, повні витрати описують взаємозалежність галузей економіки.
приклад
Розрахуємо збалансовані обсяги валових випусків галузей, використовуючи наступні дані. Для виробництва одиниці продукту X потрібно 0,1 одиниці X і 0,1 одиниці У, а для виробництва одиниці продукту У потрібно 0,9 одиниці X і 0,2 одиниці У. Обсяги споживчого попиту рівні 10 і 6.
Запишемо матрицю прямих витрат (Л), розрахуємо матрицю повних витрат (С) і знайдемо валові випуски:
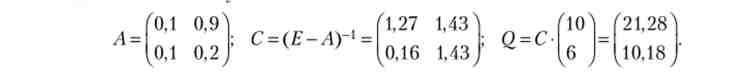
Звідси валовий випуск першої галузі дорівнює 21,28. Використовуючи елемент матриці С, ми робимо висновок, що приріст цього випуску при збільшенні товарного випуску У на 3 складе 1,43 - 3 = 4,29. Використовуючи матрицю Л, ми робимо висновок, що проміжний попит при валових випусках 40 і 10 складе 0,1 - 40 + 0,9 - 10 = 13.
Розглянемо модель Леонтьєва з цінами. Нехай задані: рА і р2 - ціни продуктів X і У. У ринковій економіці кожна галузь повинна бути прибуткова, т. е. ціна продукту повинна перевищувати сумарну вартість витрат на всі ресурси. Складемо з цих умов систему рівнянь і перетворимо її в подвійне нерівність для відносини цін:
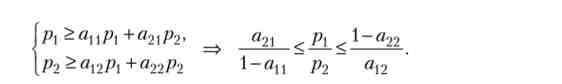
Отримане нерівність задає певний проміжок і має нескінченно багато рішень, якщо
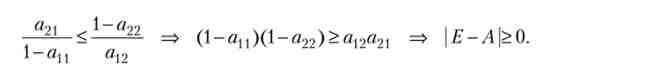
Отже, збалансоване стан ринкової економіки можна досягти лише, якщо визначник матриці (Е - А) позитивний. Такий стан не єдино: чим більше відносна вартість товару, тим вище прибутковість даної галузі. У випадках, коли відношення цін досягає межі проміжку, дохідність однієї галузі дорівнює нулю: в разі досягнення правої межі це друга галузь, в разі лівої - перша галузь.