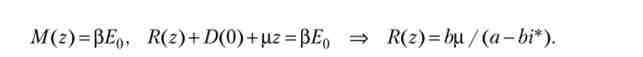| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Грошова маса в широкому розумінні (М) Складається з внутрішнього боргу (D) і рублевого еквівалента валютних резервів (R):

Внутрішній борг зростає зі швидкістю р, т. Е. D = p.
Реальний обсяг грошової маси є лінійна спадна функція внутрішньої ставки відсотка (г):

де а, b> 0; Р - дефлятор ВВП.
Якщо досягнуто паритету процентних ставок, т. Е. Немає переливу капіталу, то з наближеною формули арбітражу при низьких процентних ставках (див. Підпункті 10.1.2) отримаємо:

де Е = р / р * - паритет купівельної спроможності (див. підпункті 10.1.1), який тут ототожнюється з валютним курсом (е); р, р * - вартість кошика товарів у рублях і доларах; i * - ставка відсотка за кордоном.
Підставами (10.3) в (10.2) з урахуванням визначення ППС, ототожнюючи дефлятор ВВП і рублеву вартість товарного кошика (Р = р):
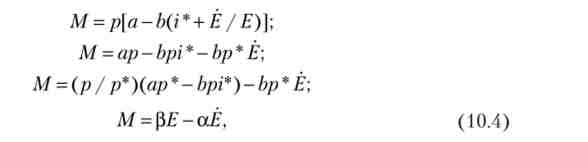
де а = Ьр * р = ар * - bp * i *.
Нехай держава підтримує фіксований обмінний курс Е0, тоді Е = 0, грошова маса незмінна, а борг зростає за рахунок скорочення валютних резервів:
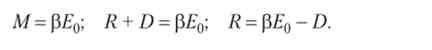
Диференціюючи останню рівність за часом. Приходимо до висновку, що валютні резерви скорочуються з тією ж швидкістю, з якою росте внутрішній борг:
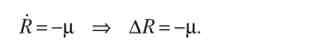
Таким чином, режим фіксованого валютного курсу неможливо зберегти з моменту часу t, для якого сумарні втрати валютних резервів (? р) більше їх початкового об'єму R (0). Знаючи це, спекулянти можуть при низькій поточної величиною валютних резервів атакувати рубль за допомогою покупки великих обсягів валюти з метою спустошити резерви держави і тим самим примусити його перейти до плаваючого обмінного курсу і девальвацію рубля. Оскільки після цього держава нездатна в короткостроковому періоді зміцнити рубль, скуплена спекулянтами валюта дозволить їм придбати більше рублів, що при незмінності цін гарантує високий прибуток.
Виконується умова «плавності» валютної атаки - фіксований курс дорівнює плаваючого курсу, який встановиться відразу після її завершення, його називають тіньовим курсом. Визначимо момент валютної атаки при заданому фіксованому курсі. З диференціального рівняння (10.4) отримаємо залежність плаваючого курсу від грошової маси, будемо шукати його рішення у вигляді лінійної функції

Підставами (10.5) в (10.4) і врахуємо, що під час відсутності валютних резервів грошова маса дорівнює внутрішньому боргу, а тому з рівності (10.1) слід: М = D = р. Отримаємо тотожність:
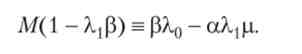
Числові коефіцієнти в обох частинах отриманої рівності дорівнюють нулю, оскільки в іншому випадку ліва частина буде залежати від змінної Л /, а права - немає. отримаємо:
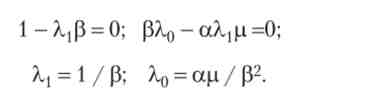
Отже, плаваючий валютний курс дорівнює
 Тоді умова «плавності» атаки на рубль:
Тоді умова «плавності» атаки на рубль:

де z - момент спекулятивної атаки.
Оскільки динаміка грошової маси відома, рівність (10.7) являє собою рівняння щодо 2, т. Е. Дозволяє розрахувати момент атаки. У режимі плаваючого курсу валютні резерви не задіяні, тому динаміка грошової маси повторює динаміку внутрішнього боргу: M (t) = D (0) + xt. Підставами цю формулу в (10.7) і вирішимо отримане рівняння:
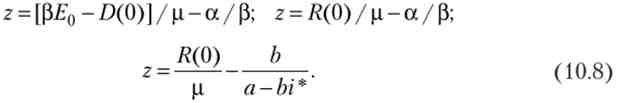
Отже, для розрахунку моменту «плавної» атаки на рубль слід розділити початковий обсяг валютних резервів на щорічний приріст внутрішнього боргу, а потім відняти від цього відносини дріб, яка залежить від ставки відсотка за кордоном і параметрів функції реальної грошової маси. Чим більше ставка за кордоном, тим більше друга дріб в правій частині останнього рівності і тим раніше слід починати «плавну» атаку. Визначимо валютні резерви до початку атаки R (z):
Отже, валютні резерви до початку «плавної» спекулятивної атаки пропорційні швидкості збільшення внутрішнього боргу і ростуть із зростанням ставки відсотка за кордоном.