| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Якщо ми з'єднаємо всі можливі комбінації оптимумів індивіда, що має початковий запас, то отримана крива «ціна-споживання» буде розташована всередині кривої байдужості, що відповідає точці відсутності торгівлі для цієї людини (рис. 8.17).
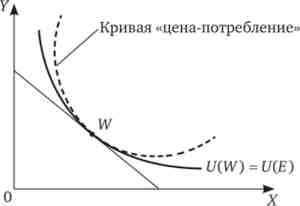
Мал. 8.17. Крива «ціна-споживання» для індивіда, що володіє початковим запасом
Тепер подивимося, як буде виглядати функція Маршалліанского попиту для індивіда, що володіє початковим запасом. Ми можемо виділити дві функції попиту. Функція попиту на оптимальний набір буде характеризувати валовий попит на товар. Це звичайна функція Маршалліанского попиту, з якою ми мали справу до сих пір. І вона приймає тільки невід'ємні значення.
Функція чистого попиту при одних цінах матиме позитивні значення, при інших - негативні (рис. 8.18). Оскільки з негативними числами важко оперувати, економісти домовилися називати функцію чистого попиту, розташовану в негативній області, функцією чистого пропозиції і давати її відображення в позитивному квадранті системи координат.
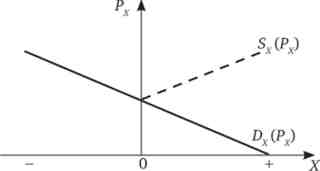
Мал. 8.18. Маршалліанскій попит на товар для індивіда, що володіє запасом
Розглянемо випадок, коли споживач до зміни ціни був чистим покупцем товару X (рис. 8.19). Його початковий набір W розташований лівіше точки оптимуму?г Чистий попит на товар X становив до зміни ціни наступну величину: Xй = Хг - Xw > 0.
Ефект заміни і ефект доходу з урахуванням зміни вартості початкового запасу
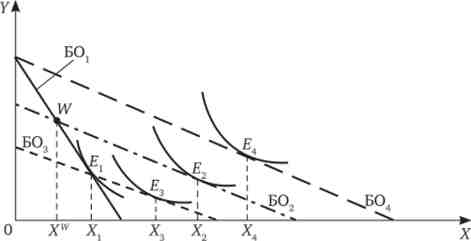
Мал. 8.19. Ефект заміни і ефект доходу з урахуванням зміни вартості початкового запасу
Нехай тепер ціна товарах знижується: Рх < Рл,. Якби індивід мав певної, незмінною сумою грошей I, то при зменшенні ціни товари лінія його бюджетного обмеження повернулася б вправо вгору уздовж осіХ: з BOj до В04. І новий оптимум споживача перейшов би в точку?4 з новим обсягом покупок Х4. Однак в розпорядженні індивіда знаходиться не конкретна сума грошей, а деяка кількість початкового запасу. Тому нова лінія бюджету повинна пройти через точку W початкового запасу - це лінія В02. І нова рівновага споживача буде досягнуто в точці Е2, де він набуває обсяг Х2. Індивід як і раніше залишається чистим покупцем товари. Загальний ефект ціни складе: ДХР = Х2 - Хг
Якщо ми хочемо розкласти ефект ціни на його складові, то нам необхідно провести додаткову лінію бюджетного обмеження, що відображає компенсацію споживачеві за різницю в цінах. Для простоти і наочності скористаємося версією Слуцького. Так як ціна товару X знизилася і підсумкове добробут індивіда вище початкового, то щоб повернути його до початкового набору Ех (Або до вихідної корисності, що відповідає набору Е, в версії Хікса), необхідно відібрати у споживача «зайві» гроші, пов'язані з підвищенням купівельної спроможності його доходу. Лінія додаткового бюджетного обмеження Б03 пройде через точку Е{ і буде паралельна бюджету Б02. Проміжне рівновагу при новій ціні товари і новому номінальному доході буде досягнуто в точці Еу
Тепер ми можемо знайти всі ефекти.
Ефект заміни показує зміну структури споживання індивіда під дією динаміки відносних цін - це перехід з точки Ej в точку Е3. Величина прямого ефекту заміни складе: AXS = Х3 -X ,.
Якби не було початкового запасу, то звичайний ефект доходу для споживача показав би перехід оптимуму з точки Е.л в ціль ?4. Тому звичайний ефект доходу складе величину: ДХ '= Х4 - Х3.
Однак оскільки змінилася вартість початкового запасу - в разі падіння ціни ця вартість знизилася, то споживач не може досягти точки?4. Його підсумкове рівновагу спостерігається в точці Е2 при обсязі покупок товарах меншому, ніж в точці?4: Х2 < Х4. Перехід з точки?4 (Віртуальної) в оптимум Е2 (Реальний) для індивіда означає зміну вартості початкового запасу. Це є ефект зміни вартості первинного запасу, або просто ефект запасу. Його величина буде дорівнює: AX1V = Х2 - Х4. В даному випадку ефект запасу негативний, що означає зниження купівельної спроможності запасу в результаті зменшення ціни товари.
Як і раніше, в сумі три ефекту дорівнюють загальному ефекту ціни:
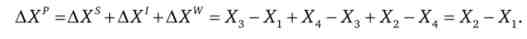
Аналогічним чином можна знайти перехресні ефекти.
Питання для роздумів
Чи може бути так, що при зниженні ціни ефект запасу буде позитивним, т. Е. Х2 > Х4? В якому випадку це можливо?
ШПАРГАЛКА
Алгоритм знаходження ефектів розкладання зміни ціни товару
в наборі з урахуванням початкового запасу (по Слуцькому)
вихідний оптимум Е1 - maxl / (X, Y) при Б01: Рх ? Xw + Ру ? Yw = Рх X + Ру ? Y.
підсумковий оптимум Е2 - maxU (X, Y) при Б02; Рх ? X 'v + PY ? Yw = Рх ?X + PyY.
проміжний оптимум Е3 - maxU (X, Y) при Боу Р, -X, + РУ - У, = Рх^ - X + Pr Y.
Віртуальний оптимум ЕЛ - тах? 7 (Х, У) при Б04: Рх - Xw + PY ? Yw = Рх Х + Ру - У.
Ефект ціни: АХР = AXS +АХ '+ AXW = Х2-Х ,.
Еффектзамени: AXS= X3-X ,.
Ефект доходу: АХ1 = Х4-Х3.
Ефект запасу: ДХ "= Х2 - Х4.
Розглянемо Маршалліанскій попит на товар X. Так як індивід володіє початковим запасом товарах, то його дохід залежить від ціни останнього. Тому Маршалліанская функція попиту буде являти собою складну функцію
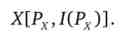
Знайдемо повний диференціал цієї функції
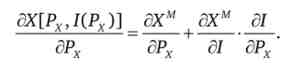
Перший доданок цього виразу являє собою звичайне рівняння Слуцького для Маршалліанской функції попиту без урахування запасу:
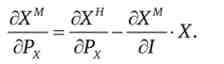
У другому доданку по лемі Шепарда, так як 1 (РХ, РУ) = РХ ?Xw +PY Y
+ Py-Yw, отримуємо: = XW, т. е. похідна доходу індивіда за ціною
8РХ
товару дорівнює початкового запасу даного товару.
Підставляємо нові вирази для першого і другого доданків у вихідне рівняння і в результаті отримуємо
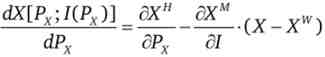
Це і є рівняння Слуцького для індивіда, що володіє початковим запасом.
В даному рівнянні
Ох "
--ефект заміни;
інх
ДХм
--X - звичайний ефект доходу;
д.I