3.1 Кількісний (кардиналістський) підхід до аналізу корисності і попиту
Кількісний підхід до аналізу корисності заснований на уявленні про можливості вимірювання різних благ в гіпотетичних одиницях корисності - Ютіліт (від англ. utility - корисність).
Зокрема, передбачається: споживач може сказати, що щоденне споживання ним 1 яблука приносить йому задоволення, скажімо, в 20 ютілов, щоденне споживання 2 яблук - 38 ютілов, щоденне споживання 2 яблук і 1 сигарети - 50 ютілов, щоденне споживання 2 яблук, 1 сигарети і 1 апельсина - 63 ютіла і т.д.
Слід підкреслити, що кількісні оцінки корисності того чи іншого товару або товарного набору мають виключно індивідуальний, суб'єктивний характер.
Кількісний підхід не передбачає можливості об'єктивного виміру корисності того чи іншого товару в Ютіліт. Один і той же продукт може становити велику цінність для одного споживача і ніякої цінності - для іншого. У наведеному вище прикладі мова йде, мабуть, про завзятого курця, оскільки додавання до 2 яблукам 1 сигарети істотно збільшило корисність товарного набору.
Кількісний підхід зазвичай не передбачає також можливості порівняння обсягів задоволення, одержуваних різними споживачами.
Економісти неодноразово намагалися позбутися від терміну "корисність", має деякий оцінний характер, знайти йому відповідну заміну. Так, відомий російський економіст Н. X. Бунге пропонував використовувати термін "придатність" (Nutze - нім.).
"Потреба в наркотичних речовинах, - писав він, - безсумнівна, але чи можна сказати, що опіум і гашиш корисні для курців, - вони тільки придатні як речовина для сп'яніння". [1] Італо- швейцарський економіст і соціолог В. Парето пропонував замінити термін "корисність" неологізмом ophelimite, утвореним ним від грецького?????????, що означав відповідність між річчю і бажанням. Французький економіст Ш. Жид пропонував використовувати термін "желаемость" (desirabilite - фр.), Вважаючи, що він "не припускає у бажання моральних чи аморальних рис, розумних або нерозважливих". [2]
В підтримку терміна "желаемость" висловлювався і відомий американський економіст і статистик І. Фішер. "Корисність, - вважав він, - є спадщиною Бентама і його теорії задоволення і страждання". [3] Фішер вказував і на перевагу антоніма "небажаність" порівняно з "безглуздістю". (Зовсім невдалий вживається в нашій сучасній літературі антонім "антіполезность"). Проте термін "корисність" пережив своїх критиків і використовується понині. Отже, в кількісної теорії корисності передбачається, що споживач може дати кількісну оцінку в Ютіліт корисності будь-якого споживаного ним товарного набору. Формально це можна записати у вигляді функції загальної корисності:
TU=F (QA, QB, ..., QZ), (3.1)
де TU - загальна корисність даного товарного набору; QA, QB, ..., QZ - обсяги споживання товарів А, В, ..., Z в одиницю часу. Велике значення мають припущення про характер функції загальної корисності. Зафіксуємо обсяги споживання товарів B, C, ..., Z. Розглянемо, як змінюється загальна корисність товарного набору в залежності від обсягу споживання товару А (наприклад, яблук). У верхній частині рис. 3.1, a зображена ця залежність. Довжина відрізка ОК дорівнює корисності товарного набору при фіксованих нами обсяги товарів В, С, ..., Z і при нульовому обсязі споживання товару А. У кількісної теорії передбачається, що функція TU у верхній частині рис. 3.1, а зростаюча (чим більше яблук, тим більшу корисність має товарний набір) і опукла вгору (кожне наступне яблуко збільшує загальну корисність товарного набору на меншу величину, ніж попереднє).
У принципі ця функція може мати точку максимуму (S), після якої вона стає спадною (уявіть, що Вас щомісяця змушують споживати по 100 кг яблук).
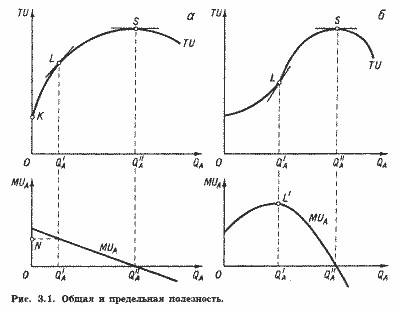
У нижній частині рис. 3.1, а зображена залежність граничної корисності яблук від обсягу їх споживання.
Гранична корисність - це приріст загальної корисності товарного набору при збільшенні обсягу споживання даного товару на одну одиницю. Математично гранична корисність товару є приватна похідна загальної корисності товарного набору (3.1) за обсягом споживання г-того товару:

Геометрично значення граничної корисності (довжина відрізка ON) дорівнює тангенсу кута нахилу дотичної до кривої TU в точці L. Оскільки лінія TU опукла вгору, із збільшенням обсягу споживання г-того товару кут нахилу цієї дотичної зменшується і, отже, знижується і гранична корисність товару.
Принцип спадної граничної корисності часто називають першим законом Госсена, по імені німецького економіста Г. Госсена (1810-1859), вперше сформулював його в 1854 р. [4] Цей закон містить два положення. Перше констатує убування корисності наступних одиниць блага в одному безперервному акті споживання, так що в межі досягається повне насичення цим благом. Друге констатує убування корисності перших одиниць блага при повторних актах споживання. Принцип спадної граничної корисності по суті аналогічний так званому основному психофізичному законом Вебера-Фехнера, [5] характеризує зв'язок між силою подразника (стимулу) і інтенсивністю відчуття. Згідно з цим законом, роздратування рівної інтенсивності, повторювані протягом певного часу, супроводжуються зниженням інтенсивності відчуттів. Принцип спадної граничної корисності полягає в тому, що із зростанням споживання якогось одного блага (при незмінному обсязі споживання всіх інших) загальна корисність, одержувана споживачем, зростає, але зростає все більш повільно. Математично це означає, що перша похідна функції загальної корисності за кількістю даного блага позитивна, а друга - негативна:
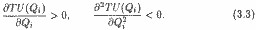
Однак принцип спадної граничної корисності аж ніяк не універсальний. У багатьох випадках гранична корисність наступних одиниць блага спочатку збільшується, досягає максимуму і лише потім починає знижуватися. Така залежність характерна для невеликих порцій подільних благ. Друга затяжка викурювали вранці сигарети, можливо, має для любителя велику корисність, ніж перша, а третя більшу, ніж друга. Така ситуація показана на рис. 3.1,6. В інтервалі від нуля до Q'A загальна корисність зростає швидше, ніж збільшується обсяг споживання блага, зростає і гранична корисність. В інтервалі від Q'A до Q'A загальна корисність зростає повільніше, ніж обсяг споживання, а гранична знижується від максимального рівня (в точці L ') до нуля.
Математично це означає, що на ділянці від нуля до Q'A і перша, і друга приватні похідні функції загальної корисності за обсягом споживання даного блага позитивні:
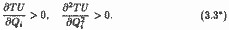
Таким чином , принцип спадної граничної корисності, або перший закон Госсена, справедливий лише в тому випадку, якщо друга приватна похідна функції загальної корисності негативна. Однак оскільки споживач купує на ринку не окремі акти споживання (у нашому прикладі-затягування), а певні блага (у нашому прикладі - сигарети), ми можемо вважати, що для обертаються на ринку товарів перший закон Госсена (3.3) виконується.
Припустимо тепер, що споживач має деяким доходом; ціни на товари A, B, ..., Z не залежать від його поведінки і дорівнюють відповідно PA, PB, ..., PZ товарного дефіциту немає; все товари є нескінченно ділимими (як, наприклад, ковбаса, вершкове масло і т.д.).
За цих припущеннях споживач досягне максимуму задоволення, якщо він розподілить свої кошти на купівлю різних товарів таким чином, що:
1) для всіх реально купуються ним товарів А, В, С, ... має місце:

де MUA, MUB, MUC - граничні корисності товарів А, В, С;? - Деяка величина, що характеризує граничну корисність грошей; [6]
2) для всіх непокупаемих ним товарів Y, Z, ... має місце:
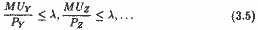
Доведемо першу частину твердження.
Припустимо протилежне: товари А і В реально купуються споживачем, але MUA / PA> MUB / PB. Для визначеності припустимо, що МUA=40 ютілов в розрахунку на кілограм, PA=2 руб. за кілограм, МUB=20 ютілов в розрахунку на кілограм, PB=4 руб. за кілограм. У результаті:
(МUA / PA=40 ютілов / 2 рубля)> (20 ютілов / 4 рубля=МUB / PB
Очевидно, що покупець при цьому не досягає максимуму задоволення. Він може скоротити споживання товару В на 1 кг, при цьому він втратить 20 ютілов. Але за рахунок зекономлених 4 руб. він може купити додатково 2 кг товару А і отримати додатково приблизно 80 ютілов. (Слово "приблизно" тут використано тому, що 2-й додатковий кілограм товару А може принести меншу корисність, ніж 1-й, скажімо, тільки 39 ютілов, а не 40).
Тому різниця між МUA / PA і МUB / PB буде скорочуватися. Перерозподіл витрат буде відбуватися до тих пір, поки відношення граничної корисності до ціни для кожного реально товару, що купується не стане однаковим.
Рівність (3.4) можна інтерпретувати в такий спосіб. Ставлення МUA / PA являє собою приріст загальної корисності в результаті збільшення витрат споживача на товар A на 1 руб.
Очевидно, що в стані оптимуму споживача всі подібні відносини для реально купуються товарів повинні бути рівні один одному. І будь-яке з них може розглядатися як гранична корисність грошей (точніше, 1 руб.). Величина А показує, на скільки ютілов збільшується загальна корисність при збільшенні доходу споживача на 1 руб.
Другу частину твердження можна довести абсолютно аналогічним чином, від протилежного. Зміст формули (3.5) полягає в тому, що якщо вже 1-й рубль, витрачений на покупку товару Z, приносить споживачу недостатньо високу корисність, то він взагалі відмовляється від споживання цього товару.
Таким чином, рівність (3.4) показує, що в оптимумі (максимум корисності при даних смаках споживача, ціни і доходи) корисність, яку видобувають із останньої грошової одиниці, витраченої на купівлю будь-якого товару, однакова, незалежно від того, на який саме товар вона витрачена. Це положення отримало назву другого закону Госсена. Звичайно, споживач може розкаятися в покупці, навіть задовольняє рівності (3.4). Це означатиме, що "за час від покупки до каяття в ній" знак в (3.4) для даного товару змінився на протилежний. [7]
Спробуємо показати тепер на основі кількісного підходу , що обсяг попиту і ціна пов'язані зворотною залежністю. Знову розглянемо рівність (3.4).
Припустимо, що ціна на купується споживачем товар А підвищилася. В результаті перше відношення в рівності (3.4) зменшилася. Щоб відновити рівність (3.4) і максимізувати загальну корисність, споживач почне скорочувати споживання товару А. Аналогічним чином будуть надходити й інші споживачі. Таким чином, з підвищенням ціни товару обсяг попиту на нього скорочується. [8]
ПРИМІТКИ
[1] Бунге Н. Підстави політичної економії. Київ, 1870. С. 20.
Микола Христофорович Бунге (1823-1895) в 1859-1880 рр.. (з перервами) - ректор Київського університету св. Володимира; в 1881-1886 рр.. - міністр фінансів; в 1887-1895 рр.. - голова Комітету міністрів; з 1890 р. - академік.
[ 2] Жид Ш. Основи політичної економії. М., 1918. С. 53.
Шарль Жид (1847-1932) - професор політичної економії Паризького університету (1898-1920).
У зв'язку з терміном "желаемость" згадайте слово "хотіння" в наведеному уривку з Ф. М. Достоєвського (див. 1.1).
[3] Fisher I. Mathematical investigation in the theory of value and price / / Transaction of the Connecticut academy. 1892. Vol. 9. July. P. 23.
[4] Книга Госсена не викликало інтересу у сучасників, і в 1858 р . автор вилучив її з продажу і знищив. Вона була перевидана в 1889 р. на основі випадково вцілілого екземпляра. Теоретики кількісної корисності високо оцінили внесок свого попередника, всіляко пропагували його ім'я.
[5] Ернст Генріх Вебер (1795-1878) - німецький анатом і фізіолог, основоположник психофізики та експериментальної психології. Густав Теодор Фехнер (1801-1887) - німецький фізик і психолог. У 1858 р. математично обробив експериментально встановлені в 1830-1834 рр.. Вебером залежності між відчуттями і зухвалими їх подразненнями.
[6] В. С. Войтінський називав цю величину "середньої граничною корисністю по бюджету покупця" (Войтінський В. Ринок і ціни: Теорія споживання, ринку та ринкових цін. СПб ., 1906. С. 120-124).
Володимир Савелійович Войтінський (1885-1960), російський економіст-математик, статистик, з 1918 р. в еміграції (Югославія, Німеччина, США).
[7] Войтінський В. Ринок і ціни. С. 125 і слід.
[8] Наведене міркування дуже нестроге. Воно не враховує можливості вже згадуваного парадоксу Гіффена . Цей парадокс буде проаналізований надалі за допомогою порядкового підходу до аналізу корисності і попиту.
Інформація, релевантна "3.1 Кількісний (кардиналістський) підхід до аналізу корисності і попиту"
- 11.3. Кількісний (кардиналістський) підхід до аналізу поведінки споживача
кількісний (кардиналістський) і порядковий (ординалістський). Представники першого (У. Джевонс, А. Маршалл) грунтуються на теорії граничної корисності. Захисники другого (В. Парето, І. Фішер) використовують теорію кривих байдужості та споживчого бюджету. Розглянемо спочатку пояснення поведінки споживача з позиції теорії граничної корисності. Корисність, або Ютіліт (англ. utility), - - Терміни і поняття
корисності Крива корисності (загальної та граничної) Закони Госсена: перший і другий кардиналістський теорія Ординалістська теорія Споживчий вибір Два правила споживчої поведінки Гранична корисність на витрачений рубль Ефект приєднання до більшості Ефект сноба Ефект Веблена Споживчі переваги Криві байдужості Карта кривих байдужості - Корисність: воскресіння кардиналізма
кількісного виміру корисності стала загальним місцем в економічній теорії і саме поняття «корисність» було визнано анахронізмом. Дійсно, підхід з позицій теорії очікуваної корисності дозволяє зробити поняття корисності «операціональним» і дати йому кількісну оцінку. Нехай індивід воліє благо А благу В, а благо В благу С (А> В> Q. Нехай йому запропоновано вибір між лотереєю, - Практикум по темі лекції 11
кількісний підхід до вимірювання корисності від порядкового підходу? Що таке «ефект доходу» і «ефект заміни»? 9. Що таке вигода споживача? Як її максимізувати? 10. Що таке рівновагу споживача? Тести, ситуації, завдання Чи вірні твердження Введення податку на продажу не зачіпає рівновагу споживача. «Ефект заміни» полягає в тому, що в результаті зміни ціни - 39. Предмет дослідження та особливості методу представників першого етапу маржинализма
кількісних, що піддаються виміру корисностей для всіх індивідів (домогосподарств) суспільства, і оптимальним вважається такий розподіл ресурсів, яке максимізувати б добробут. Еволюцію маржинальних ідей на цьому етапі можна охарактеризувати наступним чином: 1) на початку маржиналізм у своєму індивідуальному перебігу концентрував увагу на значенні економічного аналізу в частині - Ключові терміни
корисності Сукупна корисність Гранична корисність Убуваючий гранична корисність Відносні ціни Ефект доходу Ефект заміщення Закон попиту Товар Гіффена Надлишок споживача (споживчий надлишок) Вигоди чи втрати в результаті зміни - 4. ЦЕПОЧКА Джевонсом
аналізі, оскільки перехід від кривої корисності до кривої попиту вимагає важливих припущень (постійної граничної корисності грошей, незалежності між споживанням різні благ), які він вважав - РЕКОМЕНДОВАНА ЛІТЕРАТУРА
підходи, результати, межі можливостей / / THESIS. 1994. Вип. 5. С.29-80. Фрідмен М., Севідж Л. Аналіз корисності при виборі серед альтернатив, що припускають ризик / / Теорія споживчої поведінки та попиту. СПб.: Економічна школа, 1993. Стіглер Дж. Економічна теорія інформації / / Теорія фірми. СПб.: Економічна школа, 1995. С. 507-529. АкерлофДж. Ринок «лимонів»: - 5. АВСТРІЙСЬКА ШКОЛА. Теорія граничної корисності
аналізу в різних - 2. Маржиналистская теорія цінності та її переваги
підходу до економічного аналізу стала саме теорія граничної корисності. Підхід маржиналістів до теорії цінності був протилежний підходу класичної школи. Класики виводили цінність (вартість) з витрат виробництва, що визначаються у сферах виробництва і розподілу, тобто визначали її «з боку пропозиції». Навпаки, маржиналісти йшли «з боку попиту», надаючи основне - 2. Маржиналістському ТЕОРІЯ ЦІННОСТІ ТА ЇЇ ПЕРЕВАГИ
підходу до економічного аналізу стала саме теорія граничної корисності. Підхід маржиналістів до теорії цінності був протилежний підходу класичної школи. Класики виводили цінність (вартість) з витрат виробництва, що визначаються у сферах виробництва і розподілу, тобто визначали її «з боку пропозиції». Навпаки, маржиналісти йшли «з боку попиту», надаючи основне - 4. Ланцюжок Джевонса
аналізі, оскільки перехід від кривої корисності до кривої попиту вимагає важливих припущень (постійної граничної корисності грошей, незалежності між споживанням різних благ), які він вважав - Висновки
аналізу поведінки споживача визначити і зону заміщення (субституції) - ділянка кривої байдужості, в якому можлива ефективна заміна одного блага іншим. 8. Бюджетні обмеження показують за допомогою бюджетної лінії споживача, який саме набір товарів споживач вважає для себе найбільш вигідним. 9. Рівновага споживача настає тоді, коли у нього відсутні стимули - Кардиналізма і ординалізму
підхід отримав назву кардиналізма, а його прихильники стали називатися кардіналістамі. Опоненти кардіналістов - першим з них був В. Парето - заперечували можливість безпосереднього вимірювання корисності кожного блага. Найбільше, на що здатний, на їх думку, людина, - це розташувати свої переваги в порядку убування. Одиницю ж вимірювання корисності операционально визначити не можна, - Кардиналізма і ординалізму
підхід отримав назву кардиналізма, а його привер-Кснци стали називатися кардіналістамі. Опоненти кардіналістов - першим з них був В. Парето - заперечували можливість безпосереднього вимірювання корисності каж-Рдо1 про блага. Найбільше, на що здатний, на їх думку, людина, - 'Чи розташувати свої переваги в порядку убування. Одиницю Же виміру корисності операционально визначити - Корисність: воскресіння кардиналізма
кількісного виміру корисності стала загальним місцем в економічній теорії і саме поняття «корисність» було визнано анахронізмом. Дійсно, підхід з позицій теорії очікуваної корисності дозволяє зробити поняття корисності «операціональним» і дати йому кількісну оцінку. Нехай індивід воліє благо А благу В, а благо В благу С (А> В> С). Нехай йому запропоновано вибір між лотереєю, - Глава 3 Корисність, переваги, попит
кількісний і порядковий. В останній третині XIX в. У. Джевонс, К. Менгер, [3] Л. Валь-рас одночасно і незалежно один від одного запропонували кількісну теорію корисності, в основі якої лежала гіпотеза про можливість порівняння корисності різних благ. Її поділяв і А. Маршалл. Ця теорія зустріла серйозну критику. Ф. Еджуорт, В. Парето, І. Фішер [4] запропонували альтернативну