§ 2. Основні рівняння МОБ
| Проміжне споживання (галузі) | Кінцеве використання |
Всього використано |
||||||
| I | ... | j | ... | n | ||||
| проміжні потреб-ня | l | allxl | ... | aljxj | ... | alnxn | yl | xl |
| ... | ... | ... | ... | ... | ... | ... | ... | |
| i | ajlxl | ... | aijxj | ainxn | yi | xi | ||
| ... | ... | ... | ... | ... | ... | ... | ... | |
| n | anlxl | ... | anjxj | ... | annxn | yn | xn | |
| Валова додана вартість | zl | ... | zj | ... | zn | |||
| Всього ресурсів | xl | ... | xj | ... | xn | |||
Якщо розглядати дані МОБ по рядках, то кожну галузь можна описати у вигляді наступного рівняння:
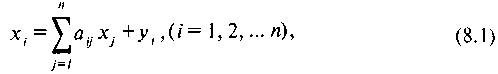
де хi - продукція i-й галузі ;
аij - коефіцієнт прямих витрат продукції i-й галузі на одиницю продукції j-й галузі (аij=хij / хj);
хj - продукція j-й галузі;
yi - кінцевий попит i-й галузі (кінцеве споживання, валове нагромадження, сальдо експорту-імпорту).
Рівняння (8.1) характеризує використання продукції кожної галузі на проміжне і кінцеве споживання, нагромадження та інші кінцеві потреби.
При розгляді МОБ по колонках кожна галузь може бути представлена наступним рівнянням:
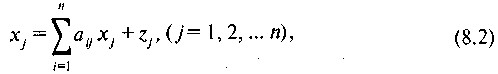
де хj - продукція j-й галузі;
zj - валова додана вартість j-й галузі.
Рівняння (8.2) характеризує вартісної складу випуску продукції кожної галузі.
В матричної формі рівняння (8.1) має вигляд:
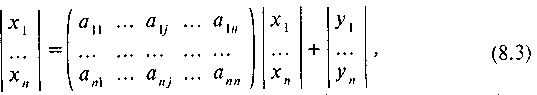
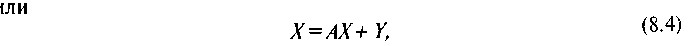
де X - вектор випуску продукції;
A - матриця коефіцієнтів прямих витрат , що дозволяє встановити прямі виробничі зв'язки між галузями;
Y - вектор кінцевого попиту.
За допомогою ЕОМ на основі цієї матриці розраховується матриця коефіцієнтів повних витрат, що показують як прямі, так і непрямі витрати на виробництво одиниці кінцевої продукції.
Найважливішою особливістю матриці коефіцієнтів повних витрат є те, що, якщо ці коефіцієнти помножити на вектор кінцевого попиту, то можна отримати випуск продукції по кожній галузі. Наведемо математичне обгрунтування цього розрахунку.
З формули (8.4) випливає, що:
Y=X - AX, (8.5)
або
Y=(E - A) X, (8.6)
де Е-одинична матриця.
Помноживши обидві частини рівняння на (Е-А) -1, отримаємо:
(E-A) -1 Y=(E - А) -1 (Е - А) Х, (8.7)
де (Е - А) -1 - матриця коефіцієнтів повних витрат.
Тоді
(Е-А) -1 Y=X. (8.8)
Рівняння (8.8) називається основним рівнянням МОБ, оскільки воно може використовуватися насамперед для прогнозування. Маючи матрицю коефіцієнтів повних витрат і перебираючи різні варіанти вектора розподілу кінцевого попиту, можна розрахувати різні варіанти прогнозу.
Розглянемо побудову МОБ на умовному прикладі. Припустимо, що економіка країни складається з трьох галузей. Взаємозв'язки між цими галузями можна простежити за їх рахунками. У даному прикладі не враховується сплата галузями податків.
Рахунок галузі 1, млн. руб.
| Дебет | Кредит | ||
| Запаси готової продукції на початок року Придбано матеріалів у галузі 2 Придбано матеріалів у галузі 3 Виплачено працівникам |
10 50 60 |
Отримано за продукцію, продану галузі 2 Отримано за продукцію, продану населенню Запаси готової продукції на кінець року |
70 70 10 |
| Всього витрат Прибуток |
140 10 |
Всього отримано | 150 |
| Разом 150 | Разом 150 | ||
Рахунок галузі 2, млн руб
| Придбано матеріалів у галузі 1 Виплачено працівникам |
70 20 |
Отримано за продукцію, продану галузі 1 Отримано за продукцію, продану галузі 3 Запаси готової продукції на кінець року |
20 70 9 |
| Всього витрат Прибуток |
90 9 |
Всього отримано | 99 |
| Разом | 99 | Разом | 99 |
Рахунок галузі 3, млн.
| Придбано матеріалів у галузі 2 Виплачено працівникам | 70 30 |
Отримано за продукцію, продану галузі 1 Отримано за продукцію, продану населенню |
50 40 |
| Всього витрат | 100 | Всього отримано Збиток |
90 10 |
| Разом | 100 | Разом | 100 |
Зв'язки, існуючі між 1, 2, 3-й галузями, можна показати за допомогою таблиці МОБ. При цьому необхідно привести у відповідність номенклатури витрат у всіх рахунках галузей, що в даному прикладі було враховано заздалегідь. МОБ з економіки, що складається тільки з цих галузей, має наступний вигляд (млн руб.):
| Галузі | Проміжне споживання | Разом | Кінцеве споживання | Валове нагромадження | Разом | Всього | |||
| 1 | 2 | 3 | |||||||
| Проміжне споживання | 1 | - | 70 | - | 70 | 70 | -. | 70 | 140 |
| 2 | 20 | - | 70 | 90 | - | 9 | 9 | 99 | |
| 3 | 50 | - | - | 50 | 40 | - | 40 | 90 | |
| Разом | 70 | 70 | 70 | 210 | 110 | 9 | 119 | 329 | |
| Оплата праці найманих працівників | 60 | 20 | 30 | 110 | |||||
| Валовий прибуток | 10 | 9 | -10 | 9 | |||||
| Разом | 70 | 29 | 20 | 119 | |||||
| Всього | 140 | 99 | 90 | 329 | |||||
З прикладу видно, що по кожній галузі ресурси (по колонках) рівні їх використанню (за строками).
Інформація, релевантна " § 2. Основні рівняння МОБ "
- 1. Фундаментальне рівняння росту
основних економічних агрегатів і тотожних перетворень виводиться фундаментальне рівняння Харрода (1) де G-темп приросту доходу або випуску продукції, Y - дохід або випуск продукції. К-капітал, S-заощадження, I - інвестиції, за визначенням рівні приросту капіталу К, за умовою рівні заощадженням; s - частка заощаджень - Модель номінального доходу
рівняння (5) - (8). Саме втора представляє внесок Фрідмена. Рівняння (5) припускає, що еластичність попиту на день | по доходу дорівнює 1. Рівняння (6) отримано в результаті нескладних перетворений ^ з рівняння Фішера, що встановлює зв'язок між реальним щ центом і темпом інфляції: при наступних умовах а! - Г=г *, q-g=к, к=const. Причому остання умова означає не * менность - 2. Для кожного даного рівня виробництва процентна ставка змінює-ся таким чином, щоб врівноважити попит і пропозицію на
основних ринків: ринку грошей та ринку това-ів. Попит і пропозиція на ринку грошей описуються рівнянням M=Kr) P, де M - пропозиція грошей, P - рівень цін, а г - чроцентная ставка. L {r) - функція, що показує, як | прос иа гроші реагує на процентну ставку. Дан-ве рівняння називається рівнянням LM (гроші - чіквідность) [Liquidity (англ.) - ліквідність; Mo-ney (англ.) - - Модель номінального доходу
рівняння (1) - (4) і грошова - рівняння (5) - (8). Саме друга і являє внесок Фрідмена. Рівняння (5) припускає, що еластичність попиту на гроші по доходу дорівнює 1. Рівняння (6) отримано в результаті нескладних перетворень з рівняння Фішера, що встановлює зв'язок між реальним відсотком і темпом інфляції: за таких умов: r=r *, q-g=k, k=const. Причому останнє - 65. Які функціональні зв'язки відображає рівняння обміну І. Фішера?
Рівняння показує, що рівень цін знаходиться в прямому взаємозв'язку з кількістю грошей і швидкістю їх обігу та в обернено пропорційній зв'язку з потоком товарів. Формула обміну Фішера допомагає чіткіше уявити функціональні зв'язки на ринках грошей і товарів. При зміні одного показника змінюються й інші. Якщо зростає грошова маса М, то при стабільності швидкості обігу денегV - Швидкість обігу грошей і рівняння кількісної теорії грошей Існує ще один напрямок застосування кількісної
рівняння кількісної теорії грошей Існує ще один напрям застосування кількісної теорії грошей. З її допомогою ми можемо спробувати дізнатися, скільки, в середньому, раз на рік кожна банкнота використовується для оплати знову вироблених товарів і послуг. Відповідь на це питання дає економічна змінна, звана швидкістю звертання-ня грошей. У фізиці поняття швидкості дозволяє оцінити - Але рівновага в долгосроч-ном і короткостроковому періодах досягається при зраді-ванні різних неременних: - У довгостроковому
основні постулати класичної еко-номічного теорії прекрасно працюють при описі функціонування економі-ки в довгостроковому періоді. Однак, як ми обговорили в попередньому розділі, ціни па багато товарів реаг-руют на зміну пропозиції грошей з великим запізненням, і загальний рівень цін не може сам по собі врівноважити попит на гроші і пропозиція грошей з короткостроковому періоді. Для - Реальна ставка відсотка коригує номінальну з урахуванням поправки на інфляцію.
Рівняння, щоб показати, що номінальна ставка відсотка дорівнює сумі реальної ставки відсотка і темпів інфляції: Номінальна ставка відсотка=Реальна ставка відсотка + Темпи інфляції. Такий вираз номінальної ставки відсотка становить інтерес, так як на формування величин в правій і в лівій частинах цього рівняння будуть діяти різні сили. Як ми дізналися в попередніх - Попит на гроші
основні концепції попиту на гроші: неокласична (монетаристської) і Кейнс-Андської. Монетаристська теорія попиту на гроші грунтується на неокласичних традиціях і успадкувала основні постулати кількісної теорії грошей, що виникла ще в XVIII в. і безроздільно панувала в економічній науці до 30-40-х років. Основний постулат кількісної теорії полягає в наступному: - Отже, буде дорівнює нулю і складаю-щая чистого експорту в нашому вихідному рівнянні, яке прийме наступний вих Y=C
рівнянні , яке прийме наступний вих Y=C + I + G. Таким чином, в закритій економіці ВВП дорівнює сумі споживання, інвестицій і державних закупівель. Щоб наочніше уявити, що це рівняння може сказати нам про роль і місце фінансових ринків, віднімемо С і G з його правої і лівої частини. Ми отримаємо: Y-C-G=I. Ліва частина рівняння (Y-С - G) являє собою доход економіки за - Розглянемо протилежність політику.
Рівняннями попиту та пропозиції: Qs=2Р, QD=300 - P. а. Знайдіть рівноважну ціну і рівноважний кіль-кість товару. б. Припустимо, що з покупців стягується на-лог Г, отже, нове рівняння попиту виглядає наступним чином: QD=300 - (P + T). Знайдіть нову рівновагу. Що відбувається: ціною, яку отримують продавці, ціною, кото-рую платять покупці, і обсягом