Завдання, які вирішуються за допомогою статистики Фішера

Крім знаходження інтервальної оцінки для р за допомогою перетворення

можна вирішити такі завдання.

1. Перевірити, чи узгоджується вибірковий коефіцієнт кореляції г з передбачуваним значенням генерального коефіцієнта кореляції р_а. Для цього, взявши рівень значущості а, перевіряємо, чи потрапляє абсолютна

величина різниці ?_r - Z_p0| в інтервал [0, -==. Якщо потрапляє, то гіпо-

V / 7-3

теза Н₀ : р = р₀ не відкидається. В іншому випадку відкидається з імовірністю помилки а.

2. Перевірити гіпотезу про однорідність коефіцієнтів кореляції.

нехай г_ь г₂...г_до - коефіцієнти кореляції, отримані з до нормально

розподілених сукупностей по вибірках з обсягами щ, п₂,..., п_до. перевіряється гіпотеза

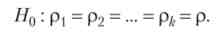
до (z_r.- z_p)²

Статистика X --г має розподіл у² з до ступенями свободи.

,= 11 / (і, - 3)

Якщо замінити z_p на середнє арифметичне

то отримаємо, що функція

розподілена за законом у} з v = k - 1 ступенями свободи. Якщо тепер для заданих а й v = k - 1

то гіпотеза однорідності відкидається з імовірністю помилки а. В іншому випадку гіпотеза 7 /₀ не відкидається.

У разі прийняття гіпотези однорідності кращою точкової оцінкою р є значення г, отримане зворотним перетворенням з z_r

регресійний аналіз - це статистичний метод дослідження залежності випадкової величини У від змінних X: (j = 1,2, k), Що розглядаються в регресійному аналізі як невипадкові величини незалежно від істинного закону розподілу Xj.

Зазвичай передбачається, що випадкова величина Y має нормальний закон розподілу з умовним математичним очікуванням Y = (Рс ^ ..., х_до), є функцією від аргументів ^, і з постійною, що не залежить від аргументів дисперсією а².

Для проведення регресійного аналізу з (k + 1) -мірною генеральної сукупності (У, Х_{, Х₂,X, ..., Х_до) береться вибірка обсягом п і кожне i-e спостереження (об'єкт) характеризується значеннями змінних (У, х_п, х, 2, ..., х,..., х), де xj - значення j-й змінної для / -го спостереження (/ = 1, 2, ..., /?), у - значення результативної ознаки для / -го спостереження.

Найбільш часто використовувана множинна лінійна модель регресійного аналізу має вигляд

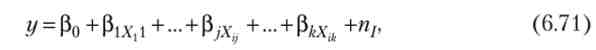
де е, - випадкові помилки спостереження, незалежні між собою, мають нульову середню і дисперсію а².

Відзначимо, що дана модель справедлива для всіх / = 1,2,п, лінійна щодо невідомих параметрів р₀, (3 ,, ..., (3 /, ..., р_{/ (>} і аргументів.

Таким чином, в лінійної регресії модельне (теоретичне, передбачене) значення У є лінійної комбінацією значень одного або більше предикторов.

Як випливає з рівняння (6.70), коефіцієнт регресії р_; показує, на яку величину в середньому зміниться результативний ознака У, якщо змінну Х_} збільшити на одиницю виміру, т. е. є нормативним коефіцієнтом.

У матричної формі регресійна модель має вигляд

де У - випадковий вектор-стовпець розмірністю (П? 1) можна побачити значень результативної ознаки (у_і г /₂, -> У ") X - матриця розмірністю п? (k + 1) | спостережуваних значень аргументів. елемент матриці х_:] розглядається як невипадкова величина (Г - 1, 2, n; j = 0, 1, 2, k); Р - вектор-стовпець розмірністю [(& + 1) - 1] невідомих, які підлягають оцінці параметрів (коефіцієнтів регресії) моделі; е - випадковий вектор-толбец розмірністю (П? 1) помилок спостережень (залишків). компоненти вектора е, - незалежні між собою і мають нормальний закон розподілу з нульовим математичним очікуванням (М_е1 - 0) і невідомої дисперсією а² (D_Kl = е²). На практиці рекомендується, щоб п перевищувало k не менш ніж у три рази.

У матричному вигляді модель У = Хр + е записується в такий спосіб:

Одиниці в першому стовпці матриці забезпечують наявність вільного члена в моделі. Тут передбачається, що існує змінна х₀, яка у всіх спостереженнях приймає значення, рівні 1.

Основне завдання регресійного аналізу полягає в знаходженні за вибіркою обсягом п оцінки невідомих коефіцієнтів регресії р₀, Р (, ..., Р /. Моделі або вектора р в моделі У = Хр + р

Так як в регресійному аналізі х розглядаються як невипадкові величини, а М_еГ = 0, то рівняння регресії має вигляд

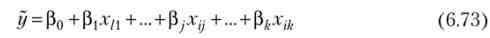
для всіх г = 1,2, ..., п, або в матричної формі

де У - вектор-стовпець з елементами у₁,..., у ,, ..., у_п.

Для оцінки вектора Р найбільш часто використовують метод найменших квадратів (МНК), згідно з яким в якості оцінки приймають вектор Ь, який мінімізує суму квадратів відхилення спостережуваних значень г /, від модельних значень у, т. е. квадратичную форму:

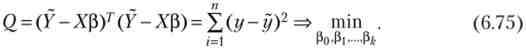
Диференціюючи квадратичную форму Q no р₀, p_lt р ^ і прирівнюючи похідні нулю, отримаємо систему нормальних рівнянь

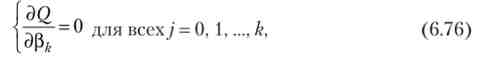
вирішуючи яку отримуємо вектор оцінок Ь, де b = (Ь₀, Ь_і Ь_до)^т.

За методом найменших квадратів вектор оцінок коефіцієнтів регресії виходить по формулі

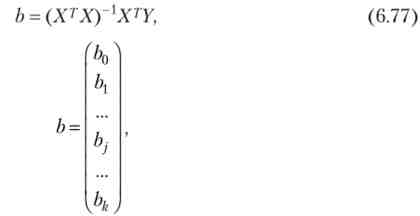
де X - транспонована матриця X; (X^r X) ¹ - матриця, зворотна матриці Х^ТХ.

Знаючи вектор оцінок коефіцієнтів регресії Ь, знайдемо оцінку рівняння регресії

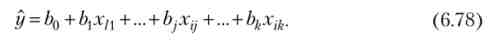
Або в матричному вигляді у = Х (3, де У = (.Vi> # 2> ---> Уп У?

Оцінка ковариационной матриці коефіцієнтів регресії вектора b визначається з виразу

де S² = -(Y-Xb)^T(Y-Xb).

n-k-1

З огляду на, що на головній діагоналі ковариационной матриці знаходяться дисперсії коефіцієнтів регресії, одержуємо

1. Динамічна функція сукупного попиту
   Побудована в параграфі 6.3 функція сукупного попиту показує, яким буде обсяг дійсного попиту при різних значеннях рівня цін. В умовах довготривалого зростання рівня цін при визначенні величини сукупного попиту потрібно враховувати два додаткових обставини, пов'язаних з тим, що величина сукупного
2. Диференціальна модель ринку праці
   Попит на працю (D ) І пропозицію праці (S) задані зворотними функціями w (t {D) і w s (S), рівноважна ставка зарплати дорівнює w. Сформулюємо три припущення моделі: 1) швидкість зміни попиту пропорційна різниці ціни попиту і рівноважної ставки зарплати: де k> 0. Якщо ціна попиту перевищує
3. Держава, поняття і цілі грошово-кредитної політики держави
   Третій важливий агент, зазвичай присутній в макроекономічних моделях, - держава. Воно розглядається в макроекономіці зазвичай як єдине ціле, без поділу на уряд і ЦБ. Передбачається, що держава діє в цілях збільшення суспільного добробуту, використовуючи інструменти фіскальної та грошово-кредитної
4. Дефляція боргу
   Ірвін Фішер (1967-1947) - вчений-бунтар і практик. Він заклав основи для фінансового моделювання міжчасового вибору, а з урахуванням тимчасових переваг поглибив розуміння дії ліквідності в умовах нарощування заборгованості і дефляції. Пізня робота Фішера, присвячена дефляція боргу, представляє
5. Біржова практика застосування теорії кредитних циклів, технологія побудови біржових торгових систем
   Ідея про те, що теорія озброює практику, з першого погляду не відноситься до біржової торгівлі і основній масі кредитних комунікацій. Однак зміни, що відбуваються у світовій економіці зажадали перегляду основних теоретичних підходів до циклічності, особливо щодо шокового впливу кредиту на
6. Балансовий метод аналізу територіальної рухливості населення
   Подання предметної області у вигляді балансової матриці з успіхом використовувалося вітчизняними та зарубіжними економістами при вирішенні найрізноманітніших завдань. Баланс руху населення є статистичну таблицю, що характеризує формування чисельності та структури населення в результаті його
7. Антиінфляційна політика
   Коли в країні інфляція досягне таких розмірів, що загрожує перерости в гіперінфляцію, тоді першочерговим завданням економічної політики уряду стає придушення інфляції. Як випливає з моделі інфляції, необхідною умовою її виникнення є прискорення темпу зростання кількості грошей, що перебувають
8. Ак-модель
   Для того щоб технічний прогрес був ендогенних, у виробників повинні бути стимули для інвестицій в нові технології. Однак в рівновазі на конкурентних ринках факторів виробництва доходи факторів збігаються з їх граничними продуктами. В силу позитивної однорідності неокласичної виробничої функції