Рівновага і стійкість

визначення рівноваги

Формально станом рівноваги в моделі IS-LM прийнято називати набір (У *, г *, С *, 5 *, Г). Цей набір являє собою ситуацію, коли рівновага встановлюється одночасно на всіх трьох ринках моделі. Зауважимо, що на відміну від найпростішої неокласичної моделі, в якій рівновагу встановлювалося на ринках послідовно (за винятком ринку продукту та фінансового ринку), тут рівновага встановлюється одночасно на всіх ринках, підкреслюючи взаємозалежність різних ринків. Ключовим моментом при визначенні рівноваги є пара (У *, г) - після того як визначені рівноважний випуск і рівноважна реальна ставка відсотка, рівноважний розподіл наявного доходу між споживанням і заощадженнями і рівноважний обсяг інвестицій визначаються автоматично. Тому часто, говорячи про рівновагу в моделі IS-LM, економісти мають на увазі саме цю пару, графічно представляє собою точку перетину кривих IS і LM (рис. 9.3).

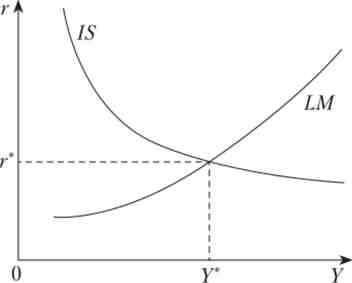
Мал. 93. Рівновага в моделі IS-LM

Стійкість. Для дослідження питання про стійкість рівноваги в моделі IS-LM слід записати диференціальні рівняння, що показують, як випуск і реальна ставка відсотка реагуватимуть на стану нерівноваги. На ринку товарів і послуг та фінансовому ринку рівняння, що показує, як повинен змінитися випуск у відповідь на нерівноважну ситуацію, буде наступним:

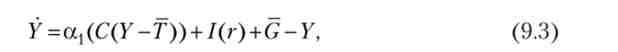
де оц > 0. Рівняння (9.3) показує, що якщо економіка знаходиться в стані (У, г), що знаходиться праворуч від кривої IS, то рівень випуску буде зменшуватися. Якщо ж точка (У, г) знаходиться зліва від кривої IS, рівень випуску буде рости.

Додамо тепер рівняння, що описує поведінку реальної ставки відсотка г у відповідь на нерівноважну ситуацію. Це поведінка визначається станом ринку грошей. А саме, якщо попит на реальні грошові залишки перевищує пропозицію, т. Е. m (Y, r)> M / Р (Точка (У, г) лежить нижче кривої LM), То реальна ставка відсотка зростає. Якщо ж точка (У, г) лежить вище кривої LM, ставка відсотка падає. Така поведінка природно описати за допомогою рівняння

де а₂ > 0.

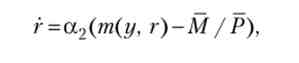
Напрямок руху в залежності від положення точки (К, г) по відношенню до кривих IS і LM схематично представлено на рис. 9.4. Дивлячись на нього, можна легко припустити, що рух буде спіралеподібним навколо положення рівноваги. Однак з цього малюнка можна зрозуміти, чи буде це спиралеобразное рух сходящимся або розбіжним. В даному випадку можна гарантувати асимптотичну стійкість, яка випливає з Пропозиції А. З (див. Математичне додаток А). Для цього потрібно лише перевірити, що у матриці

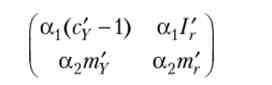
визначник більше нуля, а слід менше нуля. Легко переконатися, що це дійсно так в силу стандартних припущень про функції споживання, інвестиційного попиту і попиту на реальні грошові залишки.

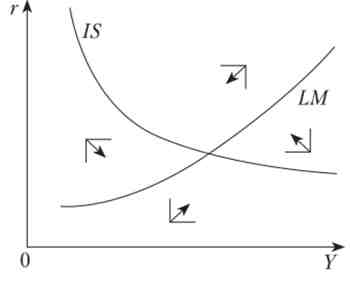
Мал. 9.4. Динаміка в моделі IS-LM

1. Стабілізаційна політика, дефіцит державного бюджету і державний борг
   Так як стабілізаційна політика зводиться до маніпулювання державним бюджетом і зміни пропозиції грошей, то її здійснення безпосередньо впливає на розміри бюджетного дефіциту і державного боргу (D), що представляє собою накопичену суму бюджетних дефіцитів: D = Х6. При наявності державного боргу
2. Способи розрахунку ВВП
   1. ВВП як додана вартість. Додана вартість - різниця між вартістю вироблених товарів і вартістю використаних сировини і матеріалів, вона складається з зарплати, відсотка, ренти і прибутку. Дані для розрахунку ВВП містяться в бухгалтерських звітах підприємств, які платять ПДВ - податок на додану
3. Споживання та інвестиції, модель з параметрами (Тобін)
   Дохід - функція капіталу: Y = К а, інвестиції (Г) дорівнюють приросту капіталу (амортизації немає), витрати складаються з витрат на закупівлю і установку капіталу: С = (Р + з 1, де р - ціна нового капіталу; с - ціна його установки. Нехай ставка відсотка - м Прибуток в період t дорівнює різниці
4. Соціальний людський капітал
   Соціальний людський капітал - сукупність довгострокових соціальних взаємодій індивіда, які впливають на його дохід або споживання. Найпростіша модель соціального людського капіталу. Є два індивіда, їх доходи (або обсяги споживання) в момент t рівні і w 2 t і виражаються вектором розподілу
5. Скандинавська модель
   Дана система виходить з активної соціальної політики, що проводиться державою, метою якої є зниження різниці в рівні життя населення. Для цього використовується податкова система, що дозволяє ефективно перерозподіляти ресурси всередині економіки. Скандинавська модель відрізняється високим
6. Схема відтворення Маркса марксизм
   - економічна теорія, в якій єдиним фактором ринкової вартості визнається фізична праця робітників. Вироблена вартість (W) за Марксом дорівнює де з - вартість зношених засобів виробництва («постійний капітал»); v - заробітна плата робітників («змінний капітал»); т - прибуток капіталістів
7. Рушійні сили глобалізації
   Глобалізація не може бути здійснена сама по собі. Процеси глобалізації світового господарства підштовхуються і направляються досягненнями як у сфері технологій, так і в області інституційного та організаційного проектування. До ключових драйверів глобалізаційних процесів можна віднести: міжнародний
8. Розрахунок показників диференціації доходів в суспільстві
   Соціально-економічні індикатори рівня життя населення є невід'ємними компонентами соціальних програм і використовуються як інструмент вимірювання результатів впливу економічних умов на рівень життя населення. Вони формуються на основі статистичних даних, що характеризують обсяг, склад, основні