| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Репрезентативне виробник пред'являє попит на фактори виробництва і виплачує їм винагороду, виробляє умовний єдиний продукт, а також інвестує. Розглянемо ці процеси докладніше.
Виробничий процес репрезентативного виробника описується виробничою функцією, яка зіставляє величиною використаного капіталу До > 0 і кількості робочої сили L > 0 випуск Y: Y = F (K, L). Відносно виробничої функції видобувних припускають, що вона:
dF
- монотонно зростає: > 0, F [> 0, де F '= -y i = {До, I};
Е /
i-> 0
історичний екскурс
Типовим прикладом функції, що задовольняє цим властивостям, є функція Кобба - Дугласа, що визначається як Y = F (K, L) = АЮ ~аЬа (А> 0,0 < а < 1).
Поява функції Кобба - Дугласа приписують таких обставин. Американський статистик Пол Дуглас, який вивчав статистику національного доходу США, зауважив, що в середньому частка доходу, що доводилася на трудові ресурси за період з 1899 по 1922 р становила 75%, а решта 25% припадали на доходи капіталу. Ці цифри відповідали оцінками продуктивності праці та продуктивності капіталу. Дуглас звернувся до колеги-математику Чарльзу Коббу з проханням запропонувати можливу функціональну залежність, і він запропонував залежність зазначеного вище виду. Раніше схожий вид гіпотетичної виробничої функції використовував шведський економіст Кнут Виксель. Кобб і Дуглас описали властивості, якими володіє запропонована ними виробнича функція, поклавши а = 3/4 і А = 1,01. Зауважимо, що ця функція задовольняє всім зазначеним вище властивостям виробничої функції.
У разі якщо величина одного з факторів, наприклад капіталу, фіксована протягом якогось періоду часу (К = К), Зручно вважати, що виробнича функція залежить тільки від однієї змінної, наприклад, кількості купа: Y = F (L) = F (K, L); тоді функція Кобба - Дугласа матиме вигляд: Y = F (L) = = AL ° (A > 0, 0 < а < 1), а її графік має вигляд, представлений на рис. 3.9.
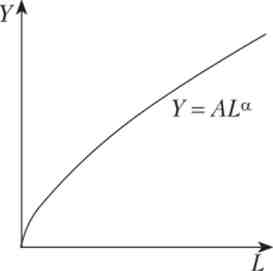
Мал. 3.9. Виробнича функція Кобба - Дугласа
При вирішенні практичного питання про вибір оптимальної кількості праці при заданій кількості капіталу (або навпаки: про вибір оптимальної кількості капіталу при заданому кількості праці) репрезентативний виробник використовує поняття граничного продукту фактора виробництва. Граничний продукт фактора виробництва являє собою приріст виробленого продукту при зміні даного чинника виробництва на одиницю (вважаючи інші фактори виробництва фіксованими). Наприклад, граничний продукт праці визначається як MPL = F (K, L +1) - F (K, I), або в безперервному випадку MPL = F [.
Вирішуючи задачу про оптимальну кількість праці при заданій кількості капіталу, репрезентативний виробник, який оперує в умовах конкурентного ринку, буде порівнювати дохід, отриманий від додаткової одиниці праці, рівний вартості граничного продукту праці, з витратами на додаткову одиницю праці в розмірі заробітної плати в одиницю часу. Якщо додатковий дохід вище, ніж витрати на додаткову одиницю праці, слід найняти додаткову одиницю праці, і навпаки. Виходить, що оптимальна кількість праці при заданій кількості капіталу визначається з рівності W = P - MPL або w = MPL, де XV - номінальна (т. е. виміряна в грошових одиницях) заробітна плата, Р - номінальна ціна виробленого продукту, a w - реальна заробітна плата, що дорівнює відношенню номінальної зарплати XV до рівня цін Р. Аналогічна ситуація з капіталом, витрати на який вимірюються через так звану рентну ціну капіталу - витрати на придбання капіталу плюс відсоток, очікуваний власником капіталу за період, якщо передбачається, що капітал зношується протягом періоду, або просто відсоток на капітал, якщо передбачається, що він використовується нескінченно довго.