4.2 Пряма еластичність попиту за ціною
Пряма еластичність попиту за ціною характеризує відносну зміну попиту на i-тий товар при зміні його ціни . Коефіцієнтом прямої еластичності попиту за ціною називають відношення відносної зміни обсягу попиту у відсотках до відносного зміни ціни:
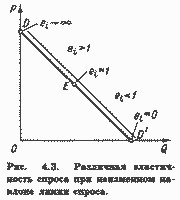
Оскільки, як правило, обсяг попиту зі збільшенням ціни знижується,?? Q i /?? P i < 0.
Щоб уникнути негативних чисел, перед правою частиною (4.3) часто вводять знак мінус.
Розрізняють точкову і дугову еластичність. Точкова еластичність (або еластичність в точці) характеризує відносну зміну обсягу попиту при нескінченно малій зміні ціни:
Якщо крива попиту задана лінійною функцією, наприклад Q i=ai - bp i, нахил її, очевидно, буде Q i /?? P i=-b. Підставляючи останній вираз в (4.4), отримаємо:
ei=- bi (P i / Q i) (4.5)
Це означає, що коефіцієнт еластичності буде різним в різних точках такої кривої, незважаючи на один і той же її нахил. Графічно коефіцієнт точкової еластичності лінійної кривої попиту визначається співвідношенням відрізків кривої, що лежать вище і нижче, що цікавить нас точки.
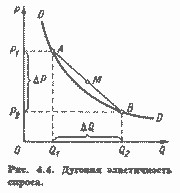
Звернемося до рис.4.2.
Очевидно, що?? P=P 1 P 2=Q 1 Q 2=E 1 F, P=OP 1, Q=OQ 1. При малих змінах Р і Q?? Р=dP і?? Q=dQ. Тоді:
ei=(?? Q i /?? P i) (P i / Q i)=(Q 1 Q 2 / P 1 P 2) (OP 1 / OQ 1)=(FE 1 / FE) () P 1 / OQ 1).
З подоби трикутників EFE 1 і E 1 Q 2 D слід:
FE 1 / FE=Q 1 D / Q 1 E=Q 1 D / OP 1 ,
звідки:
ei=(Q 1 D / OP 1) (OP 1 / OQ 1)=Q 1 D / OQ 1. З подоби трикутників DP 1 E і EQ 1 D слід: Q 1 D / ED=P 1 E / ED=OQ 1 / ED. Таким чином, в точці Е:
ei=Q 1 D / OQ 1=ED / ED. (4.6)
Якщо точка Е знаходиться в середині лінії попиту (рис.4.3), то, як випливає з (4.6), в цій точці ei=1. Лівіше її e i> 1, правіше - e i <1. У точці D ei -???, В точці D ei=0.
Таким чином, коефіцієнт прямої еластичності попиту за ціною може приймати будь-які значення в інтервалі:
Про? e i? .
При цьому нахил лінійної кривої попиту залишається, за визначенням, незмінним на всьому її протязі (рис. 4.3).
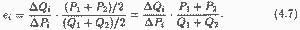
Проте частіше ми зустрічаємося зі значними змінами ціни і обсягу попиту. У цьому випадку, як очевидно, формула (4.4) взагалі непридатна для розрахунку коефіцієнта еластичності, а використання формули (4.3) дасть різний результат залежно від того, який з двох рівнів ціни і обсягу ми приймемо при визначенні другого співмножника її правій частині. Повернувшись до рис. 4.2, зауважимо, що тут можливі принаймні два рішення, що призводять до різних результатів:
ei=(?? Q i /?? P i) (P 1 / Q 1) або ei=(?? Q i /?? P i) (P 2 / Q 2)
Для того щоб уникнути невизначеності в розрахунках, використовують один з двох стандартних методів.
Або в розрахунку коефіцієнта еластичності використовують найменші значення ціни та обсягу, в нашому прикладі тоді:
ei=(?? Q i /?? P i) (P 2 / Q 1)
або використовують їх середні для інтервалу значення. У цьому випадку говорять про дугової еластичності. Дугова еластичність визначається як середня еластичність, або еластичність в середині хорди (точка М на рис.4.4), що з'єднує дві точки.
Практично використовуються середні для дуги АВ значення ціни і обсягу попиту:
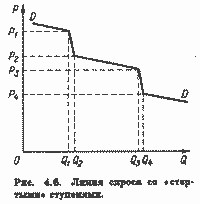
Використання (4.7), очевидно, дозволяє визначити лише приблизне значення еластичності по дузі АВ на кривій попиту. Помилка буде тим більше, чим більш увігнутою до початку координат виявиться насправді дуга АВ.
Коефіцієнт еластичності використовується для найбільш загальної характеристики попиту.
Якщо ei=0, попит зовсім нееластичний, ніяка зміна ціни не впливає на обсяг попиту.
Якщо ei=??, Попит абсолютно еластичний, мале підвищення ціни веде до нескінченно великого скорочення попиту. І навпаки, найменше зниження ціни веде до нескінченно великого збільшення обсягу попиту.
При ei=1 кажуть, що попит має одиничну еластичність, зміна ціни на 1% веде до зміни обсягу попиту також на 1%. У цьому випадку крива попиту має форму равнобочной гіперболи.
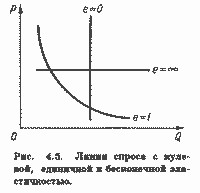
Лінії попиту з нульовою, одиничної і нескінченної еластичністю показані на рис.4.5.
Якщо 0
Відсутність товарів-замінників зумовлює досконалу нееластичність попиту (наприклад, попит на кухонну сіль). Тому, чим більше агрегированную групу товарів ми розглядаємо, тим нижче еластичність попиту (наприклад, попит на м'ясопродукти менш еластичний, ніж попит на ковбаси, а попит на ковбаси менш еластичний, ніж попит на ковбасу певного виду).
Еластичність залежить також від різноманітності можливостей (напрямів) використання даного товару. Чим різноманітніше ці можливості, тим вище і еластичність (наприклад, попит на універсальне устаткування більш еластичний, ніж на спеціалізоване).
Пряма еластичність попиту залежить також від ступеня насичення потреб. Якщо майже всі сім'ї вже мають хоча б по одному холодильника, невелике зниження ринкової ціни навряд чи істотно позначиться на обсязі попиту і продажів. Навпаки, на стадії початкового насичення попиту, скажімо, на комп'ютери, порівняно невелике зниження ціни може викликати значне зростання попиту і продажів.
Нарешті, еластичність попиту залежить від фактора часу.
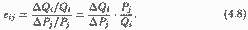
Поряд із звичайною ступінчастою лінією попиту нерідко використовують в ціновій політиці криву попиту з "стертими" ступенями. Така лінія показана на рис.4.6. Вона не має горизонтальних ділянок, її щаблі як би кілька стерті. Тому на відміну від звичайної ступінчастою кривої обсяг попиту змінюється при будь-якому як завгодно малій зміні ціни.
Проте змінюється по-різному. Наприклад, зниження ціни з P 2 до P 3, меншу, ніж зниження ціни з P 1 до P 3, супроводжується значно більшим збільшенням обсягу попиту.
Крива попиту з "стертими" ступенями пояснює таке явище, як стабільність (іноді її називають "липкостью") цін в умовах, коли ціни багатьох інших товарів змінюються. Справа в тому, що підвищення ціни даного товару з P 3 до P 2 призведе до скорочення попиту майже в 2 рази, тоді як її зниження з P 3 до P 4 дає мізерно малий його приріст. Таким чином, попит на даний товар може виявитися досить еластичним при підвищенні ціни, але майже нееластичним при її зниженні (або навпаки).

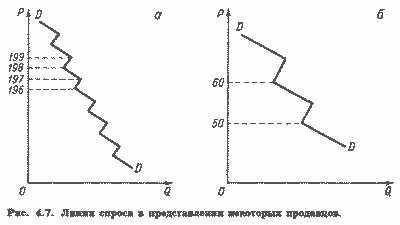
Уявлення продавців про еластичність попиту на продавані ними товари можуть виявитися досить своєрідними, що позначиться і на їх цінової стратегії. Багато з них вважають, що крива попиту має "зубці", це робить її схожою на пилку (рис.4.7), так що характер залежності обсягу попиту при русі вздовж кривої постійно змінюється.
Деякі з них вважають, що покупців більше приваблюють ціни, виражені непарними числами. Як видно на рис.4.7, а, обсяг попиту при ціні 197 більше, ніж при цінах 196 або 198 руб. Інші вважають, що обсяг попиту при цінах, виражених круглими цифрами, менше, ніж за будь-якої іншою ціною в межах певного інтервалу (рис.4.7, б). Існують і інші уявлення про характер функцій попиту і його еластичності, які служать психологічною основою для інших стратегій ціноутворення.
Інформація, релевантна " 4.2 Пряма еластичність попиту за ціною "
- Ключові терміни
еластичний попит Нееластичний попит Абсолютно нееластичний попит Попит одиничної еластичності Помилка перенесення властивостей частини на ціле Перехресна еластичність попиту за ціною Взаємозамінні і взаємодоповнювані товари Еластичність попиту по доходу Нормальні і нижчі товари Предмети розкоші і предмети першої необхідності Еластичність пропозиції за ціною Короткострокові - Еластичність попиту
еластичності попиту. Поняття еластичності попиту розкриває процес адаптації ринку до змін в основних факторах (ціні даного товару, ціною інших товарів, доходів споживачів і т.д.), що визначають попит. Розглянемо спочатку коефіцієнт еластичності попиту за ціною - показник чутливості обсягу попиту до зміни його ціни. Він визначається як відношення процентної зміни обсягу - Терміни і поняття
еластичний, нееластичний попит, одинична еластичність) Коефіцієнт еластичності попиту за ціною Пропозиція Закон зміни пропозиції Крива пропозиції Коефіцієнт еластичності пропозиції Еластичність пропозиції (одинична еластичність, еластичне, нееластичне пропозицію) Рівновага на ринку Ціна Рівноважна ціна «Ціна статі» і «ціна стелі» Ціна попиту і ціна - Терміни і поняття
еластичний, нееластичний попит, одинична еластичність) Коефіцієнт еластичності попиту за ціною Пропозиція Закон зміни пропозиції Крива пропозиції Коефіцієнт еластичності пропозиції Еластичність пропозиції (одинична еластичність, еластичне, нееластичне пропозицію) Рівновага на ринку Ціна Рівноважна ціна «Ціна статі» і «ціна стелі» Ціна попиту і - 9.2.5.3. ЕЛАСТИЧНІСТЬ ПРОПОЗИЦІЇ У короткий період
еластичності пропозиції. Еластичність пропозиції за ціною характеризує відносну зміну пропозиції i-го товару при зміні його ціни. Коефіцієнтом прямої еластичності пропозиції за ціною називають відношення відносної зміни обсягу пропозиції у відсотках до відносного зміни ціни. Для характеристики перехресної еластичності пропозиції вводиться додатковий - Тема 14. ЕЛАСТИЧНІСТЬ ПОПИТУ І ПРОПОЗИЦІЇ
еластичності. Попит і пропозиція залежать від зміни ціни, однак ступінь залежності окремих товарів різна. Дана особливість товарів враховується допомогою розрахунку еластичності. Еластичність - швидкість реакції попиту або пропозиції на зміну ціни. Якщо її виразити у вигляді процентних змін, то можна розрахувати коефіцієнт еластичності: {foto32} де Еdp-коефіцієнти - Аналогічно, при русі з точкм В в точку А ціна знижується на 40%, а кількість возра- постає на 40%. В обох
еластичність спро-са за ціною дорівнює 1. Якщо у вас виникне необхідність розрахувати еластичність, пам'ятайте про метод середньої точки. У цій книзі ми будемо не так часто звертатися до даного ме-Тодуа. Для наших цілей сутність еластичності - ре-акція обсягу попиту на зміну ціни - більш важлива, ніж її розрахунок. Види кривих попиту Зазвичай економісти класифікують криві попиту в - 1.3.4. Еластичність попиту та пропозиції
еластичність попиту - ступінь зміни попиту у відповідь на 1% зміни ціни. Визначення коефіцієнта цінової еластичності попиту:, де Ed - коефіцієнт цінової еластичності,? Qd (%) - процентна зміна обсягу попиту,? P (%) - процентна зміна ціни. або або, де Q1 - первинний об'єм попиту, Q2 - змінений - Резюме
еластичність спро-са, вимірює чутливість обсягу попиту на товарка зміни ціни даного товару Вона определяетсякак ставлення процентного зміни обсягу спро-са до процентної зміни ціни. 2. Значення еластичності попиту за ціною вздовж лінійної (прямолінійною) кривої попиту змінюється. Онависока при високій ціні і низька при низькій ціні 3. Якщо еластичність попиту перевищує 1, то - Терміни і поняття
еластичність попиту Коефіцієнт цінової еластичності попиту Перехресна еластичність попиту Еластичність попиту по доходу Гранична корисність Закон спадної граничної корисності Крива байдужості Карта байдужості Гранична норма заміщення Бюджетна лінія Крива - Еластичність пропозиції
еластичність пропозиції за ціною. Мірою цієї зміни є коефіцієнт еластичності пропозиції, що розраховується як відношення обсягу пропозиції (%) до зростання цін (%), тобто за формулою Fs _ Процентне зміна S Процентне зміна? 'Де Ер - коефіцієнт еластичності пропозиції; S-пропозиція; Р - ціна. Еластичність пропозиції служить показником відносної зміни - Наприклад, продукти харчування, як широ-кая товарна категорія, мають практично нееластичним
еластичним попитом, оскільки Глава 5. Еластичність та її застосування 115 не мають замінників. Морозиво - вужча товарна категорія - облада-ет і більш еластичним попитом, так як його простіше замінити іншими десертами. Занільное морозиво, дуже вузька категорія, характеризується досить еластичним. Просом, так як інші види морозива - практично досконалі його суб-: титут.