Оптимальний вибір індивіда між дозвіллям і роботою

Для аналізу оптимального вибору індивіда між дозвіллям і роботою ми можемо застосувати відомий нам інструментарій дослідження поведінки споживача - максимізацію функції корисності при бюджетному обмеженні.

Функція корисності індивіда в цьому випадку може бути представлена двома способами. Споживач здійснює вибір між набором споживчих товарів З, що продаються по нормованої ціною Р (Яку для простоти можна прирівняти до одиниці: Р = 1), і вільний час (R) або часом роботи (L). У першому випадку, оскільки вільний час являє благо для індивіда, вибір здійснюється між обсягами двох благ. У другому випадку, так як час роботи ми вважаємо антиблаго (тут мається на увазі робота не як самореалізація людини, а як ті її складові частини, які супроводжуються певними труднощами і незручностями), вибір буде пов'язаний з набором блага і антиблаго. Заробітна плата (w) є ціною одиниці як праці (часу роботи), так і вільного часу (в якості альтернативних витрат вільного часу).

Таким чином, вибір індивіда на ринку праці пов'язаний з максимізацією функції корисності: U - U (C, R) або U - U {C, L). причому

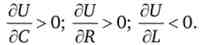
Якщо немає яких-небудь додаткових характеристик, то в загальному випадку функція корисності може бути представлена у вигляді стандартних переваг - кривих байдужості, опуклих до початку координат (для двох благ) або опуклих вправо (для блага і антиблаго) (рис. 18.1).

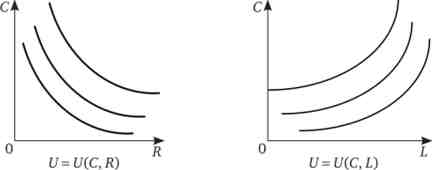
Мал. 18.1. Функція корисності для індивіда, що здійснює вибір між роботою і вільним часом

Індивід здійснює вибір при наявності двох обмежень. По-перше, сукупна час роботи і відпочинку не може перевищувати природного ліміту часу (наприклад, 24 години на добу, 7 днів на тиждень і т. д.). Але в дійсності це тимчасове обмеження набагато менше. Відносно часу, необхідному для підтримки життєдіяльності людини, індивід не може робити вибір між роботою і відпочинком. Час, необхідний на сон і харчування, не входить в область економічного вибору, оскільки тут мова йде про самого життя людини. Таким чином, тимчасове обмеження індивіда має вигляд

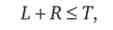
де Т - загальний ліміт часу, що виділяється на роботу і відпочинок.

По-друге, слід брати до уваги бюджетне обмеження. Витрати індивіда - це придбання набору споживчих благ: З? Р. Доходами служать два види джерела грошей: 1) загальний трудовий дохід, який заробляє в результаті оплати часу роботи: I - w; 2) інші доходи, не пов'язані з часом роботи (дивіденди по цінних паперах, спадок, доходи від нерухомості і т. д.): 1₀.

Тому бюджет споживача виглядає так: З? Р = L? w + /₀ або для двох благ: C-P = (T-R) -w + I₀<^>Rw + CP = T- w + I₀ - індивід «купує» вільний час і споживчі товари за рахунок внетрудовой доходу і грошової оцінки загального часу, наявного в його розпорядженні.

Графічно оптимум індивіда знаходиться як точка дотику лінії бюджетного обмеження і відповідної кривої байдужості. У координатах блага і антиблаго ця точка показує оптимальний обсяг праці (рис. 18.2), а в координатах двох благ - оптимальний обсяг вільного часу (рис. 18.3).

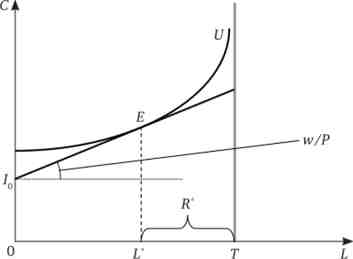
Мал. 18.2. Оптимум індивіда: вибір часу роботи

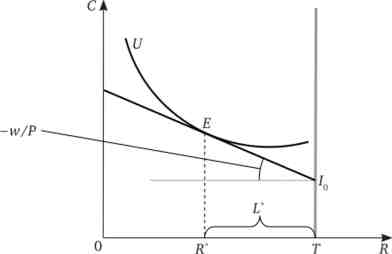
Мал. 18.3. Оптимум індивіда: вибір вільного часу

Слід зазначити, що нахил лінії бюджетного обмеження відповідає величині реальної заробітної плати (W / P).

Як і у випадку зі звичайним вибором споживача, рівновагу індивіда тут спостерігається при рівності грошових вартостей і граничнихкорисностей благ:

де MU_R, MU_C - гранична корисність відповідно вільного часу і товарного набору.

Таким чином, реальна заробітна плата в рівновазі для споживача означає величину граничної корисності дозвілля, поділену на значення граничної корисності споживчих благ.

З цієї рівності, враховуючи, що вільний час і час роботи в сукупності не перевищують Т годин, і беручи до уваги бюджетне обмеження, можна знайти конкретні значення вільного часу, часу роботи, товарного набору, індексу цін і заробітної плати для оптимального стану споживача.

Для пошуку оптимального рішення можна використовувати метод Лагранжа.

Завдання, що ілюструє теорію

Споживач розподіляє 18 год між роботою і вільним часом. Фірма, де працює даний індивід, надає своїм працівникам негрошові послуги (безкоштовний відпочинок, безкоштовні обіди в офісі, безкоштовне медичне обслуговування). Всі ці види внетрудовой доходу складають для даного індивіда 120 руб. Ставка заробітної плати дорівнює 50 руб. на годину. Ціна споживчих товарів дорівнює 1 руб. Функція корисності має вигляд: U (C, R) = fCR (Де С - обсяг споживчих товарів; R - число годин вільного часу в день).

• 1. Скільки годин на день споживач буде працювати?
• 2. Як зміниться його пропозицію праці, якщо ставка заробітної плати зросте до 60 руб / год?
• 3. Що станеться з пропозицією праці індивіда, якщо при ставці заробітної плати в 50 руб. його внетрудовой дохід скоротиться до 100 руб.?

Рішення

1. Запишітьм функцію корисності через L. Оскільки R = 18 - L, то U (C, L) = VC (18-I).

При обмеженні: wL + I₀ = PC.

при Р = 1 можна записати це рівняння в наступному вигляді: wL +1₀ - З = 0. Складемо функцію Лагранжа

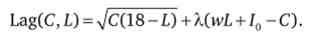
Вирішуємо отриману функцію методом Лагранжа:

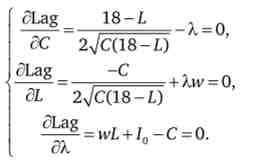
Із системи рівнянь отримуємо

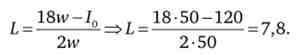
Індивід буде працювати 7,8 ч в день.

2. В умови змінюється значення заробітної плати (iv = 60). тоді

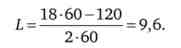
Тепер індивід буде працювати більше - 9,6 ч в день. Зростання заробітної плати стимулював працівника до збільшення часу роботи.

3. Підставами в функцію оптимального часу праці нового значення:

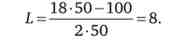
Час роботи збільшився до 8 год в день.

1. Рівняння Слуцького
   У точці оптимуму споживача Хіксіанскій і Маршалліанскій попити рівні: Знайдемо, яким чином буде змінюватися Хіксіанскій попит при зміні ціни одного з товарів (наприклад, ціни одиниці товарах) і незмінності інших параметрів 51 де (Р Р U) Нам відомо (лема Шепарда), що = - xj_n - = х. Тому отримуємо
2. Рівновага на ринку праці
   Оскільки ринок праці тісно пов'язаний з ринком продукту, в залежності від поєднання структур обох цих ринків можливі чотири базові ситуації рівноваги на ринку праці. Крім того, додаткові складності вносить діяльність профспілки - монополії на ринку праці. Формування рівноваги на ринку праці
3. Рівновага і ефективність: теореми добробуту, характеристики рівноваги конкурентних ринків
   Розглянемо ситуації існування, єдиності та стабільності рівноваги конкурентних ринків. Існування рівноваги. Максимізація корисності споживачами і максимізація прибутку конкурентними фірмами дозволяє вивести функцію надлишкового попиту: Zj = z ^ p), яка є безперервною і однорідної нульової
4. Ринки з асиметричною інформацією, інформація як економічне благо
   Бійся данайців, навіть дари приносять. Вергілій Марон Публій, поет Стародавнього Риму Після вивчення цього розділу студенти будуть: знати особливості інформації як економічного блага; вміти аналізувати поведінку індивіда і фірми в умовах нерівномірного розподілу інформаційних потоків; володіти
5. Реакція фірми на зростання ціни капіталу
   Аналогічні міркування можна використовувати при дослідженні реакції самокерованої фірми на зміну ціни капітальних ресурсів. По теоремі про неявну функцію, реакція оптимальної зайнятості на зростання або падіння ціни капіталу (ставки відсотка) може бути знайдена так: Чисельник дробу дорівнює
6. Продукт фактора виробництва
   Якщо зафіксувати обсяг одного з ресурсів, наприклад капіталу, на якому-небудь рівні (К = const), то зміна другого фактора виробництва (кількості праці) дозволяє фірмі виділити корисні для неї характеристики виробництва. Загальний обсяг випуску, вироблений в цих умовах, буде називатися сукупним
7. Премія за ризик
   Розглянемо докладніше функцію корисності індивіда, не схильну до ризику (рис. 10.3). Візьмемо лотерею з двома наслідками і / 2 ), і нехай р - ймовірність успішного результату. Лінія, що з'єднує точки на кривій корисності, що відповідають цим двом наслідків, показує можливі лінійні комбінації
8. Попит в мікроекономіці, попит і обсяг попиту
   Задамося питанням: чому люди купують ті чи інші товари та послуги? Бажання покупців придбати якийсь товар залежить від цілого ряду чинників: ціни даного товару (Р) і цін інших товарів (Р про, P h ,...), Доходів покупців і, звичайно ж, їх смаків і уподобань. При зміні значень зазначених факторів