Функція прибутку і пропозиція многопродуктовой фірми

Якщо фірма виробляє безліч продуктів, то випуск кожного товару буде змінюватися в залежності від динаміки цін на конкретному продуктовому ринку. Тому в даному випадку доцільно записати функцію сукупного прибутку фірми як функцію цін:

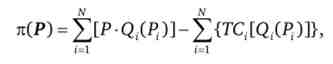
де Р - вектор цін; Р. - ціна i-ro товару на конкурентному ринку; Q. (P.) - обсяг випуску i-ro товару фірмою; TC.tQ.CP.)] - витрати випуску i-ro товару; N - число продуктів, вироблених фірмою.

Ця функція прибутку має ряд властивостей, використання яких необхідно в мікроекономічному аналізі для прогнозування реакції фірми на зміну ринкових цін.

1. Функція прибутку є зростаючою за цінами готової продук-

р. " дк (Р) БТГ (Р)

ції і спадної за цінами ресурсів: -> 0 і-< 0.

ДЦ 8w_t

Це властивість випливає з завдання оптимізації, максимізації прибутку і мінімізації витрат. Якщо товарні ціни зростають, то фірма може отримати більше прибутку за рахунок збільшення виручки навіть при незмінному випуску. Якщо ціни ресурсів збільшуються, то витрати фірми зростають, прибуток скорочується.

2. Функція прибутку однорідна нульової ступеня щодо цін: п (кр) = кк (Р) для до> 0.

Якщо помножити всі ціни на одну і ту ж позитивну величину, то постановка задачі від цього не зміниться. Цільова функція зросте на цю ж константу. Тому і рішення також буде більше на цю величину. Реальні показники діяльності фірми не зміняться. Зазнають змін тільки номінальні величини. У фірми немає грошової ілюзії.

3. Функція прибутку опукла за цінами.

Візьмемо два вектора цін (Р_} і Р₂), При яких знайдемо оптимальні рішення задачі максимізації прибутку - вектори обсягів продажів Qj і Q₂. Нехай вектор цін Р є лінійною комбінацією двох вихідних векторів: Р = кр_г + (1 -к) Р₂, 0к<1. Припустимо, що вектор Q є оптимальною комбінацією обсягів продуктів, що випускаються фірмою при цінах Р.

Так як вектор Q_L дає фірмі максимальну сукупну прибуток при цінах Р_х, то будь-який інший вектор обсягу не може принести великий прибуток: я (Р,) = Р_х Q, > Р, Q. А так як вектор Q₂ дає фірмі максимальний прибуток при цінах Р₂, то будь-який інший вектор обсягу не може принести більш високий прибуток: л (Р₂) = Р₂ Q₂ > P₂Q.

Домножим перша нерівність на до, а друге на (1 - к) і складемо

або

А це і є визначення опуклості.

4. Лемма Хотеллінга: = Q (Р).

ін, '

Зміна функції прибутку за ціною i-ro товару дорівнює функції пропозиції цього товару.

Розглянемо динаміку максимального прибутку за умови, що змінюється тільки ціна i-ro товару

Максимум прибутку означає, що фірма вже вибрала оптимальні обсяги випуску і ^ = 0 для всіх i е [1; N]. Тому: = Q, (p) -

8P_t сР,

Лемма Хотеллінга має два цікавих слідства.

Безперервна, двічі диференційована функція характеризується инвариантностью змішаних друге приватних похідних. Тому для функції пропозиції фірми (якщо виконуються зазначені умови) буде спостерігатися рівність перехресних цінових ефектів: aQ, (P) dQ / P)

8Pj ~ ад

Так як функція прибутку опукла за цінами, її другі похідні невід'ємні. Застосовуючи властивість опуклості і лемму Хотеллінга,

5Q, (P) б²л (РХ "_, _л

отримуємо: - ^ - > 0. Пропозиція фірми є неубивающей функцією за ціною.

1. Монополія на ринках промислових товарів
   Багато ринків промислових товарів складаються з двох ніш: 1) первинне виробництво; 2) переробка. Наприклад, на ринку алюмінію і інших металів ми знаходимо первинну виплавку і переробку металобрухту. Якщо ніша первинного виробництва часто виявляється монополізованої тією чи іншою фірмою, то
2. Монополістична конкуренція
   Ринок з монополістичною конкуренцією - це ринок з великим числом учасників, але з диференційованим продуктом. З одного боку, наявність диференційованого продукту призводить до виникнення певної ринкової влади кожної фірми. Кожна фірма, випускаючи свій особливий товар, має особливу нішу в вигляді
3. Модель Курно з приблизною варіаціями
   Якщо одна з фірм ринку олігополії змінює обсяг продажів, то решта компанії починають реагувати на це тільки тоді, коли ця зміна торкнеться сукупна пропозиція і відповідно ринкову ціну. Однак кожен учасник ринку може діяти трохи на випередження, передбачаючи можливі дії конкурента. В цьому
4. Міжчасовий вибір індивіда і фірми, модель міжчасового вибору при стабільних цінах
   Для того щоб визначити, яким чином індивід і фірма будуть вести себе на фінансовому ринку, чи будуть вони виступати в якості позичальника грошей або кредитора, необхідно проаналізувати межчасовий вибір. Інструментарієм для дослідження особливостей міжчасового вибору є теорія прийняття рішення
5. Максимізація темпів зростання фірми
   Діяльність менеджерів може також оцінюватися в залежності від того, наскільки швидко фірма зростає, в якій мірі збільшується її випуск з року і рік, які темпи зростання досягаються нею в довгостроковому періоді. Швидкість розширення фірми залежить від тієї частини прибутку, яка повертається
6. Квазілінійну переваги
   Додаючи деяку частину другого (нелінійного) товару, залишаючи при цьому кількість першого (лінійного) товару незмінним, споживач переходить на більш високу криву байдужості, форма якої збігається з формою попередньої кривої. У попередньому параграфі було показано, що при вирішенні задачі оптимізації
7. КПВ для економіки є кілька ресурсів
   До сих пір передбачалося, що в КПВ виводиться для економіки, в якій використовується один ресурс - праця. Однак ресурсів в ній значно більше. Тепер поставимо завдання дослідити криву виробничих можливостей економіки, в якій застосовується два типи ресурсів - праця і капітал. Вони можуть як
8. Класифікація видів фірм
   Для того щоб розібратися в світі фірм, необхідно розбити компанії на деякі групи відповідно до ряду критеріїв. 1. Види фірм за технічними характеристиками : ? однозаводскіе і многозаводскіх фірми; ? характеристика типової виробничої функції: функція Кобба - Дугласа: Q (K, L ) = До і ? 1 |!