| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Олігопольна ринок зручний для аналізу з використанням особливого математичного інструментарію - теорії ігор. Гра в економіці - це будь-який інтерактивну взаємодію, в якій учасники (гравці) мають можливість вибирати свої дії з декількох варіантів.
для Спершу розглянемо терміни, які застосовуються в теорії ігор.
найчастіше розуміється прибуток. Однак можуть бути й інші варіанти. У разі двох учасників результат гри для гравця «по горизонталі» (в табл. 15.6 гравець 2) записується першим (виділено курсивом), Результат гравця «по вертикалі» (гравець 1) вказується другим.
Таблиця 15.6. Платіжна матриця для двох гравців
|
гравець 1 |
|||
|
А |
В |
||
|
гравець 2 |
А |
СО; 1) |
(2; 2) |
|
В |
(3; 0) |
0; 3) |
|
Кожен гравець (кожна фірма) може вибирати стратегію А чи стратегію В. Гравці можуть приймати рішення одночасно, тоді ми маємо одночасну гру, або послідовно, тоді перед нами послідовна гра.
Припустимо, що в нашому випадку рішення приймаються одночасно. Який варіант своєї поведінки вибере кожен гравець?
Хоча рішення приймаються одночасно, гравці заздалегідь знають матрицю результатів. У цьому розділі ми маємо справу виключно з іграми при повній інформованості учасників. Деякі ігри з асиметричною інформацією будуть розглянуті в гл. 17.
Передбачається також, що мета кожного гравця - вибрати таку стратегію, яка принесе йому найвищий можливий результат, т. Е. Максимальний прибуток.
Будемо міркувати з позиції гравця 1. Гравець 1 дивиться на те, що вважатиме за краще гравець 2. Якщо гравець 2 обере стратегію А, то для гравця 1 оптимальний варіант - стратегія В, так як при її виборі прибуток гравця 1 буде вище: 2 > 1. Якщо гравець 2 обере стратегію В, то оптимальною для гравця 1 виявиться знову-таки стратегія В: 3 > 0. Значить, який би варіант не вибрав гравець 2, гравець 1 завжди буде дотримуватися однієї і тієї ж стратегії (в нашому випадку стратегії В). Така стратегія називається домінантною стратегією. Та стратегія, яка ніколи не буде обрана, яким би не була поведінка партнерів по грі, оскільки вона супроводжується гіршим результатом для гравця, називається домінованих стратегією. Для гравця 1 стратегія В - домінантна, стратегія А - домінованих.
Будемо тепер грати за учасника 2. Він дивиться на можливі дії гравця 1 і вибирає свій оптимальний варіант. Якщо гравець 1 вибере стратегію А, то для гравця 2 кращою виявиться стратегія В: 3 > 0. Якщо гравець 1 вибере стратегію В, оптимальної для гравця 2 буде стратегія А: 2 > 1. Таким чином, у гравця 2 немає домінантною стратегії. Він вибирає варіант своєї поведінки в залежності від того, що робить гравець 1.
Але ми знаємо, що гравець 1 обов'язково вибере стратегію В! Отже, гравець 2 обов'язково вибере стратегію А. І результат гри буде (2; 2).
Такий результат гри - це рівновага Неша (або рівновага Неша). Рівновагою Неша (Неш-рівновагою) Називається набір стратегій (а *), є єдиним для кожного гравця і максимізує цільову функцію одного гравця при незмінній оптимальної стратегії іншого гравця.
Історична довідка
Джон Неш (Нар. 1928 г.), американський математик, що працює в області теорії ігор та диференціальної геометрії. Лауреат Нобелівської премії з економіки 1994 р за аналіз рівноваги в теорії некооперативних ігор. Закінчив університет Карнегі - Меллона і Прінстонський університет, де займався хімією, міжнародною економікою і математикою. Розробив теорію ігор з ненульовою сумою. Викладав в Массачусетському технологічному інституті. Працював в корпорації RAND, що займається аналітичними і стратегічними розробками для уряду США. В даний час продовжує займатися математикою в Прінстонському університеті. Джону Нешу присвячений фільм «Ігри розуму».
В теорії олігополії рівновагу Неша є така стратегія фірми, яка максимізує її прибуток, так що:
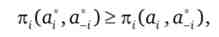
де а * - оптимальна стратегія i-й фірми; А_( - оптимальні стратегії всіх інших фірм на ринку; а. - інша, відмінна від оптимальної стратегія i-й фірми.
Неш-рівновагу показує таку ситуацію на ринку, коли ні в однієї фірми немає стимулів змінювати своє поточне поведінку ні в якісному, ні в кількісному відносинах.
У точці рівноваги Неша виконуються перше і друге умови максимального прибутку:
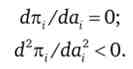
Концепція рівноваги Неша використовується для визначення рівноваги на ринку олігополії, зокрема для виведення функцій реакцій фірм.
Функцією реакції називається оптимальну поведінку даної фірми у відповідь на будь-яку поведінку будь-якої іншої фірми ринку. За визначенням, функція реакції виводиться на основі першої умови оптимальності фірми (максимуму прибутку):
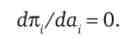
Звідки отримуємо
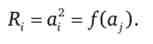
Розглянемо повний диференціал функції реакції
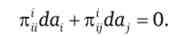
Перегруппіруем складові
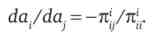
Ліва частина цього виразу показує нахил функції реакції. З другої умови максимального прибутку ми знаємо, що
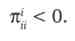
Тому нахил функції реакції цілком визначається знаком я |. (Друга змішана похідна функції прибутку).
Якщо я*. < 0, нахил функції реакції буде негативним. Збільшення дії однієї фірми призведе до скорочення прибутку іншої фірми. Подібні дії називаються стратегічними субститутами.
Якщо я1'. > 0, нахил функції реакції буде позитивним. Збільшення дії однієї фірми призведе до зростання прибутку іншої фірми. Подібні дії називаються стратегічними комплементами.
Що ж таке я!.?
ч
Розглянемо докладніше цей вислів:
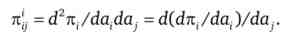
Воно являє собою додатковий прибуток, одержуваний i-й фірмою в результаті додаткового дії j-й фірми.
Питання для роздумів
Чи завжди існує рівновага Неша в одночасній грі?
Повернемося до нашої гри. Нехай тепер рішення приймаються гравцями не одночасно, а послідовно. Припустимо, що першим робить хід гравець 1, а потім свій варіант вибирає гравець 2. Платіжна матриця залишається колишньою. Чи змінить щось нове правило гри в її рівновазі?
Послідовні ігри зручніше представляти у вигляді дерева гри (Рис. 15.7). Намалюємо варіанти стратегій для кожного гравця у вигляді гілок. Точки розгалуження стратегій називаються вузлами. У нашій грі один вузол буде на першому етапі і два - на другому. Результат гри можна записати під кожним кінцевим результатом. Першим записують результат для гравця, чий хід був першим. Тут - це гравець 1.
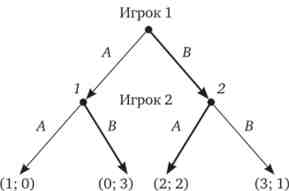
Мал. 15.7. Дерево послідовної гри
Для такого класу ігор пошук рівноваги починається з кінця, шляхом зворотного індукції (Backward induction). Припустимо, гравець 2 знаходиться у вузлі 1. Який варіант своєї поведінки він обере? Звичайно, даний гравець віддасть перевагу стратегію В, оскільки це в підсумку дасть йому великий прибуток: 3 > 0. Відзначимо його оптимальну стратегію з цього вузла потовщеною лінією. А якщо гравець 2 виявився в вузлі 2? Тоді його оптимальна стратегія - варіант А, так як саме тут він отримає максимальний прибуток: 2 > 1. Відобразимо і тут оптимальну стратегію гравця 2 потовщеною лінією.
Тепер повернемося до гравця 1. Приймаючи рішення, він знає, що при попаданні в вузол 1 гравець 2 обере стратегію В, а при попаданні в вузол 2 гравець 2 обере стратегію А. Значить, у гравця 1 насправді вибір буде між результатами (0; 3) і (2; 2). оскільки 2 > 0, гравцеві 1 краще, щоб гравець 2 виявився в вузлі 2. Тому для гравця 1 оптимальної буде стратегія В (Теж відзначимо її потовщеною лінією). Таким чином, Неш- рівновагу в даній грі - це стратегія В для гравця 1 і стратегія А для гравця 2 з результатом (2; 2).
Легко перевірити, що якщо першим рішення приймає гравець 2, а другим - гравець 1, підсумковий результат не зміниться. Але необов'язково, що завжди відбувається так.
Теорія ігор має велике економічне додаток. Зупинимося на одній з найбільш важливих сфер застосування теорії ігор - аналізі картельних угод олигополистов.