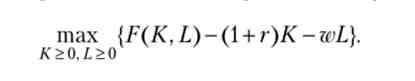w, вирішуючи завдання| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
На модель Рамсея можна поглянути не тільки як на модель оптимального економічного зростання, але і як на модель загального міжчасового рівноваги. У такій постановці завдання ми розглядаємо взаємодію споживчого і виробничого секторів економіки в умовах досконалої конкуренції і знаходимо положення рівноваги цієї ринкової системи.
Виробничий сектор в економіці представлений одним репрезентативним виробником, який задається виробничою функцією F (K, I). Цей виробник максимізує прибуток при заданій ставці відсотка г і ставки заробітної плати
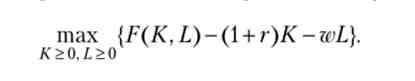w, вирішуючи завдання
Споживчий сектор економіки представляє один репрезентативний споживач, який задається миттєвої функцією корисності і (з) І коефіцієнтом дисконтування (3 (аргументом миттєвої функції корисності, як і раніше, є питоме споживання в деякому періоді). Цей споживач є власником всієї робочої сили і одержувачем всього доходу з капіталу. Цільова функція репрезентативного споживача збігається з цільовою функцією центрального планувальника в оптимизационной версії моделі Рамсея, і являє собою дисконтовану суму корисності на нескінченному проміжку вре-
оо
мени, Yfitu(ct) - Ця цільова функція максимізується при деяких t-про
природних обмеженнях, які ми зараз опишемо.
Припустимо, що до кінця періоду t-1 заощадження репрезентативного споживача складають в реальному обчисленні величину St_x = st_xLt_v де Lt_x - це сумарна кількість робочої сили в періоді t-1, a st_x - питомі заощадження (вся ця робоча сила належить нашому репрезентативному споживачеві). При цьому може виникнути питання, що розуміється під постійним темпом приросту робочої сили у єдиного агента. Справа в тому, що зазвичай репрезентативний споживач інтерпретується як одне домогосподарство або сім'я. У цьому випадку цілком обгрунтовано включати в модель нескінченно живе споживача з приростом робочої сили. Ці заощадження споживач позичає фірмам в періоді t, отримуючи дохід на капітал але реальної ставки відсотка rv так що до кінця цього періоду заощадження перетворяться в суму (1 + rt) st_xLt_x. Крім того, споживач отримує заробітну плату wtLt (Зауважимо, що тут неявно передбачається, що ринок праці завжди знаходиться в рівновазі: в кожен момент часу t зайнятість збігається з пропозицією робочої сили Lt). Таким чином, весь дохід репрезентативного споживача до кінця пери
^ 1 + г
о так t дорівнює (L + rt) st_xLt_x +wtLt = -st_x+wt Lt. Якась частина цього
(Д + / 7 )
доходу буде спожита, Ct = ctLr а решта буде являти собою заощадження на кінець періоду t, St = stLt.
Тим самим бюджетне обмеження репрезентативного споживача в періоді t виглядає наступним чином:
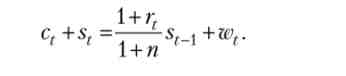
Це бюджетне обмеження має виконуватися для всіх моментів часу. Крім того, необхідно накласти ще одну вимогу, яке зазвичай називається умовою No-Ponzi Game, або умовою неприпустимості будівництва фінансових пірамід. Для випадку нескінченної траєкторії воно має вигляд (див. Математичне додаток В, параграф В.2):
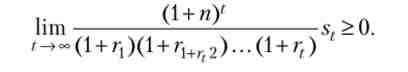
Якби умова такого типу не накладалося, то бюджетне обмеження взагалі не було б обмеженням, оскільки протягом нескінченно довгого періоду часу можна було б забезпечити як завгодно великий рівень споживання просто за рахунок постійно зростаючого в розмірі боргу. Дійсно, при описі поведінки споживача ми не накладали ніяких обмежень на розмір заощаджень, тому формально заощадження могли б бути негативними, т. Е. Споживач міг брати в борг. Трохи забігаючи наперед, зауважимо, що якби ми наклали на заощадження умови невід'ємності, нічого не змінилося б. У стані рівноваги заощадження будуть позитивними незалежно від того, чи вважаємо ми їх невід'ємними чи ні.
Отже, завдання репрезентативного споживача при відомому початковому значенні питомих заощаджень ^ записується в такий спосіб:
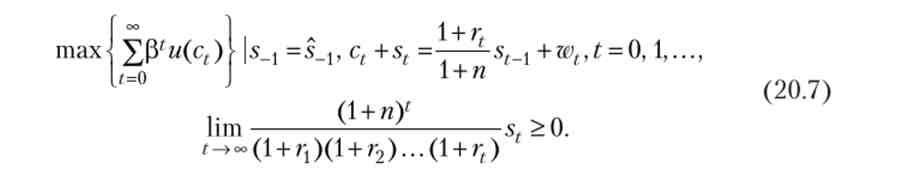
Введемо тепер визначення рівноважної траєкторії в моделі Рамсея. послідовність (Kf, c *ns *t_lfr *, w *t)t = 0 l називається рівноважної траєкторією в моделі Рамсея (що виходить із початкового стану &0 > 0), якщо &Q =&о, і виконуються наступні умови:
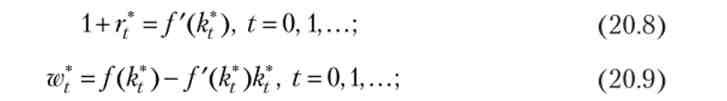
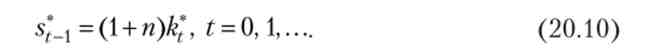
(4)
У рівновазі репрезентативний виробник вирішує свою задачу максимізації, визначаючи попит на капітал (умова 1). У припущенні досконалого передбачення всіх майбутніх ставок відсотка і заробітних плат, репрезентативний споживач вирішує свою задачу максимізації (умова 3), визначаючи плановані послідовності споживання і заощаджень (пропозиції капіталу). У рівновазі попит на капітал і пропозиція капіталу повинні бути рівні (умова 4). Умова 2 висловлює рівновагу на ринку праці. Підкреслимо, що рівновага на всіх ринках в усі майбутні моменти часу встановлюється в початковий момент часу.
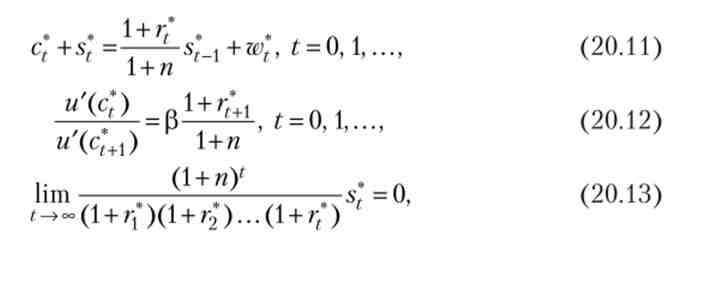
Умова 3, що визначає рівновагу в моделі Рамсея, можна переписати через необхідні і достатні умови для вирішення оптимізаційної задачі споживача (див. Пропозиція В.2 в математичному додатку В): де $ *! = (1 + n) kQ. Як і в оптимизационной версії моделі Рамсея, необхідні і достатні умови являють собою набір бюджетних обмежень (20.11), умов першого порядку (20.12) і умова трансверсальності (20.13).
Найважливішу роль в теорії загальної економічної рівноваги грають перша і друга теореми економіки суспільного добробуту. вони
говорять про те, що при деяких умовах рівновагу, що встановилось ринку, буде оптимальним, а будь-який оптимальний стан можна уявити як рівновагу. Для розглянутої нами моделі дві теореми економіки добробуту можна коротко (хоча і не цілком строго) сформулювати наступним чином: рівноважна і оптимальна траєкторія суть одне і те ж.
Дійсно, нехай (&*, с, s *t_u г *, w *t)t = 01> - рівноважна траєкторія
в моделі Рамсея (яка виходить із початкового стану> 0). тоді послідовність (K *yc *t)r = 0 { є оптимальною траєкторією в моделі Рамсея (що виходить із того ж початкового стану k0 > 0). Щоб переконатися в цьому, по-перше, підставами умови рівноваги (20.8) - (20.10) в бюджетні обмеження (20.11). Ми негайно отримаємо, що на рівноважної траєкторії виконуються умови (20.3), які в даному випадку можна інтерпретувати як рівновага на ринку кінцевого продукту (вся випущена в періоді t продукція ділиться на споживання і фізичний капітал на наступний період): з] + (1 + рр)&*+1 = t = 0, 1, ... По-друге, зауважимо, що з умов (20.8) і (20.12) випливають умови першого порядку (20.4) для оптимальної траєкторії. Нарешті, по-третє, з рівності (20.12) випливає, що
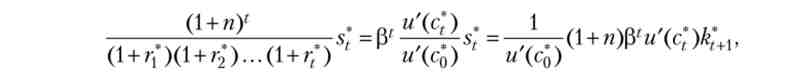
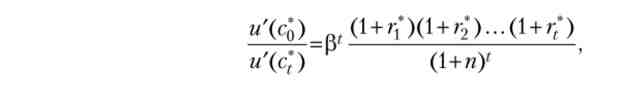
а тоді
де в останній рівності враховано умову рівноваги 4. Переходячи до межі при З ^> оо і користуючись умовою трансверсальності (20.13) ми приходимо до умови (20.5). Тим самим ми показали, що послідовність (&*, c*t)t = 0д, що фігурує у визначенні рівноважної траєкторії, задовольняє необхідним і достатнім умовам оптимальності (20.3) - (20.5), а значить, є оптимальною траєкторією.
Аналогічним чином, неважко переконатися в справедливості зворотного затвердження. якщо послідовність (K *y c *)t = 0i , яка виходить із початкового стану &Q> 0, є оптимальною траєкторією в моделі Рамсея, то послідовність (? *, ct, s *t_v rf ,iзадаваемая для всіх t = 0,1, ... равенствами
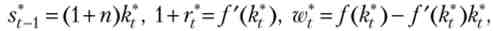
є рівноважною траєкторією, що виходить із &0 > 0.
Як завжди, нас цікавлять стаціонарні рівноваги, т. Е. Рівноважні траєкторії з постійними в часі КАПИТАЛОВООРУЖЕННОСТЬ, споживанням, заощадженнями, заробітною платою та ставкою відсотка:
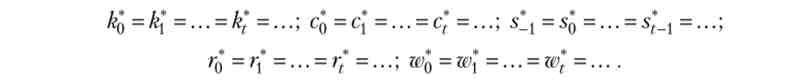
Як видно з (20.12), ставка відсотка в стаціонарному рівновазі моделі Рамсея повинна бути такою, щоб виконувалося рівність
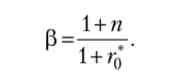
Тоді з (20.8) відразу ж слід, що стаціонарна капиталовооруженность є капиталовооруженность модифікованого «золотого» правила kMGR. Таким чином, стаціонарне рівновагу в моделі Рамсея єдино, і повністю визначається КАПИТАЛОВООРУЖЕННОСТЬ «золотого» правила. Більш того, користуючись відповідним властивістю оптимальної траєкторії, ми можемо зробити висновок, що будь-яка рівноважна траєкторія в моделі Рамсея з плином часу сходиться до стаціонарного рівноваги: при для будь-якої рівноважної траєкторії
(? *, С *, s *t_v г *, w *t)t = 01 справедливо
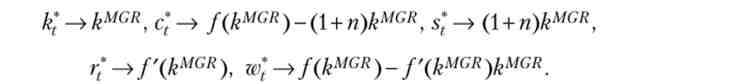
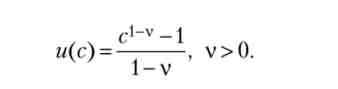
На закінчення нашого розгляду моделі Рамсея, скажемо кілька слів про можливі шляхи її узагальнення. Перш за все, можна припустити наявність технічного прогресу, і замість стаціонарних траєкторій розглянути траєкторії збалансованого зростання в моделі Рамсея, на яких все натуральні питомі (на душу населення) показники ростуть одним і тим же темпом. Однак для цього потрібно накласти деякі додаткові вимоги на пристрій функції корисності. Тому при розгляді моделі Рамсея з технічним прогресом зазвичай використовують функції корисності спеціального виду, які називаються функціями з постійною еластичністю міжчасового заміщення:
У граничному випадку V-> 1 ми приходимо до логарифмічною функції корисності: і (с) = 1нс (цей результат можна отримати, перейшовши до межі при v-> 1 у формулі для і (з) І застосувавши правило Лопіталя).
Для таких функцій корисності можна ввести в модель Рамсея трудодобавляющій технічний прогрес, зростаючий постійним темпом. За аналогією з моделлю Рамсея без технічного прогресу, можна опрсделіть оптимальні і рівноважні траєкторії і помітити, що вони суть одне і те ж. В даному випадку має місце збіжність таких траєкторій до відповідних траєкторіях збалансованого зростання. Темп зростання економіки (капиталовооруженности праці і споживання на душу населення) повністю визначається екзогенно заданим темпом зростання технічного прогресу.
важливо запам'ятати
Цікаве і популярне останнім часом напрямок досліджень в рамках моделі Рамсея пов'язано з урахуванням неоднорідності економічних агентів. Вивчена нами версія моделі спирається на припущення про наявність репрезентативного споживача. При цьому передбачається, що властивості цього репрезентативного споживача, який зазвичай інтерпретується як все «суспільство» в цілому, якимось чином агрегує всі переваги та інші параметри кожного з учасників «суспільства». Такий підхід зручний з технічної точки зору, але викликає деякі питання з змістовної точки зору. Можливість в явному вигляді врахувати те, що агенти в економіці можуть відрізнятися один від одного, з'являється, якщо розглядати модель Рамсея з декількома типами нескінченно живуть споживачів, що розрізняються своїми міжчасового уподобаннями (коефіцієнтами дисконтування). Таке узагальнення моделі Рамсея дозволяє, серед іншого, досліджувати питання про розподіл доходу всередині самого суспільства, а отже і про вплив нерівності на процеси економічного розвитку і зростання.
Крім того, за допомогою моделі Рамсея можна аналізувати вплив тієї чи іншої макроекономічної політики на економічне зростання. Наприклад, можна ввести в розглянуту модель держава, яке проводить фіскальну політику: здійснює держзакупівлі, збирає податки і встановлює розмір державного боргу. При деяких розумних припущеннях - зокрема, якщо податки збираються по неискажающим акордною (паушальною) системі - можна показати, що на стаціонарній рівноважної траєкторії в моделі Рамсея з державою капиталовооруженность, споживання і заощадження на душу населення не залежать від величини державного боргу. Це означає, що в рамках моделі Рамсея має місце рікардіанську еквівалентність (див. Гл. 17) - міжчасового поведінку споживачів залежить тільки від величини держзакупівель, але не залежить від розміру державного боргу. Якщо агентам дати можливість інвестувати не тільки в запас капіталу, але і в боргові зобов'язання держави (під ту ж ставку відсотка), то дефіцит бюджету і розмір держборгу ніяк не вплинуть на рівноважну величину заощаджень.