| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Функція корисності не є лінійної. Прирівняємо нулю похідну функції (2.147) по ЗА з урахуванням рівності (2.146) і визначення математичного очікування:

Коваріація - характеристика статистичного зв'язку двох випадкових змінних, що дорівнює різниці математичного очікування їх творів і твори їх математичних очікувань:
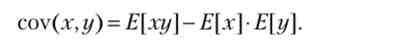
Так, зростання і вага студентів групи пов'язані позитивної зв'язком (ковариация позитивна), а число пропусків лекцій та екзаменаційна оцінка зазвичай пов'язані негативною зв'язком (ковариация негативна). З визначення ковариации слід основну властивість ковариации.
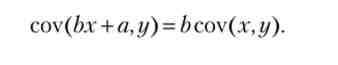
приклад
Мінлива х з однаковою ймовірністю приймає значення 2 і 4, а змінна у - значення 6 і 8. Тоді твори змінних в двох станах рівні 12 і 32, їх середнє - 22. Середні значення змінних рівні 3 і 7, їхній колективний витвір - 21, звідси ковариация дорівнює 22-21 = 1. Вона позитивна, так як більшому значенню однієї змінної відповідає більше значення іншої змінної.
Замінимо математичне очікування змінних в правій частині (2.149) сумою твори їх очікуваних значень і коваріації, використовуючи основну властивість ковариации:
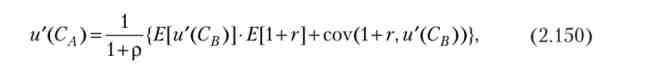
де ковариация в найпростішому випадку двох рівно можливих станів розраховується за формулою
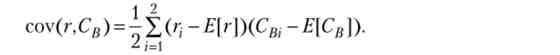
З рівності (2.150) випливає, що знак коваріації грає важливу роль у визначенні умови рівноваги споживача.
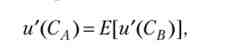
Окремий випадок 1. Нехай коефіцієнт коваріації дорівнює нулю, а середня ставка прибутковості ризикового активу дорівнює нормі міжчасового переваги (г = р), тоді умова рівноваги (2.150) набуде вигляду
т. е. очікувана гранична корисність доходу в старості дорівнює граничної корисності доходу в молодості. Дана умова схоже з відомим в мікроекономіці умовою рівноваги споживача в разі одномоментного споживання їм двох продуктів рівній ціни: їх граничні корисності повинні бути рівні між собою.
Окремий випадок 2. Розглядається квадратична функція корисності:

де для споживача, нс схильного до ризику, виконано а> 0, а для споживача, схильного до ризику, - а 0.
Спростимо (2.150) з урахуванням основного властивості ковариации і отримаємо вираз для очікуваної прибутковості ризикового активу:

Розглянемо безризиковий актив з гарантованою нормою віддачі, яка дорівнює незмінній ставці відсотка i. Оскільки його прибутковість незмінна, коефіцієнт коваріації з будь-яким іншим показником дорівнює нулю і рівність (2.151) набирає вигляду

Віднімемо (2.152) з (2.151), отримаємо умову рівноваги у вигляді

Вибравши оптимальний обсяг заощаджень в молодості, споживач може домогтися виконання умови (2.153) і тим самим максимізувати свою теперішню корисність (2.145). Для випадку з квадратичною функцією корисності отримуємо висновки з рівності (2.153):
приклад
З'ясуємо, чи є обраний споживачем обсяг заощаджень рівноважним. Він не схильний до ризику, параметр квадратичної функції корисності (А) позитивний і дорівнює 0,01. Стани різновірогідні (/ ;, = р2 = 0,5), можливі норми прибутковості ризикового активу - 12% і 18%, можливі розміри пенсії - 80 і 89. Ставка відсотка - 10%. Заощадження в молодості рівні 8, тоді обсяг споживання в старості для першого стану дорівнює Звх = 80 + 1,12 * 8 = 88,96, для другого - ЗВ 2 = = 89 + 1,18-8 = 98,44. Гранична корисність в першому стані дорівнює і '(Свх) = 1 - -0,01 - 88,96 = 0,1104, у другому - 0,0156.
Розрахуємо очікувану норму прибутковості ризикового активу, значення коваріації і очікуване значення граничної корисності (табл. 2.1).
Споживання і ризикові активи
Таблиця 2.1
|
стан |
Р |
Y |
г |
б'В |
Д г |
АСВ |
Д Гасв |
w (Св) |
|
перше |
0,5 |
80 |
0,12 |
88,96 |
-0,03 |
-4,74 |
0,1422 |
0,1104 |
|
Друге |
0,5 |
89 |
0,18 |
98,44 |
0,03 |
4,74 |
0,1422 |
0,0156 |
|
середнє |
- |
- |
0,15 |
93,7 |
0 |
0 |
0,1422 |
0,063 |
|
показник |
- |
- |
т |
ЄСп |
- |
- |
СО v (r, З л) |
Е [исв) 1 |
Перевіримо виконання умови рівноваги (2.153), використовуючи дані таблиці. Його ліва частина дорівнює 0,15 - 0,13 = 0,02, а права частина дорівнює 0,01 - 0,1422 / 0,063 = = 0,0226. Права частина більше лівої частини, тому заощадження перевищують рівноважний рівень. При скороченні заощаджень зменшаться значення Звх, ЗВ 2, ковариация і чисельник дробу, а граничні корисності і знаменник збільшаться. В результаті дріб зменшиться, і при деякому значенні заощаджень обидві частини рівності (2.153) зрівняються і споживач досягне рівноваги.