§ 1. ЗАГАЛЬНІ ПРИНЦИПИ МЕТОДОЛОГІЇ
В основі цих розрахунків лежить метод товарів-представників, суть якого полягає в наступному.
ВВП країн, що беруть участь в порівняннях, підрозділяють на деяке число товарних груп, званих у спеціальній літературі найменшими товарними групами. На практиці кількість цих груп зазвичай коливається від 150 до 300. Найменші товарні групи, створені виключно для переоцінки ВВП в порівнянну валюту, можуть об'єднуватися в більш широкі аналітичні групи з метою проведення економічного аналізу.
Для кожної найменшої товарної групи підбирається деяке число ідентичних товарів-представників з цінами (зазвичай 4-6 товарів-i представників, проте в кожному окремому випадку число товарів-представників залежить від величини дисперсії індексів цін) і обчислюються індекси цін, що характеризують співвідношення між цінами товарів-представників. Якщо наприклад, для товарної групи ЛГподобрано 5 товарів-представників, то необхідно обчислити 5 індексів цін.
За результатами попереднього етапу розрахунків для кожної найменшої товарної групи обчислюється середній індекс цін за формулою середньої геометричної невиваженою. Вибір цієї формули обумовлений двома обставинами. Невиважена формула застосовується у зв'язку з тим, що на практиці відсутні дані про ваги товарів-представників, тобто дані про частку товарів-представників у тій чи іншій товарній групі. Використання геометричної формули обумовлено тим, що вона забезпечує дотримання важливого вимоги до індексів - вимоги незалежності індексу від вибору базисної країни. Іншими словами, якби застосовувалася формула середньої арифметичної, то отриманий результат залежав би від того, яка з двох зіставляються країн (А і В) розглядалася як базисна.
Нижче наведено приклад розрахунку середнього індексу цін для найменшої товарної групи X.
| Товари-представники | 1 | 2 | 3 | 4 | 5 | |
| Ціни в країні А | 2 | 4 | 1 | 5 | 7 | |
| Ціни в країні Б | 3 | 8 | 3 | 10 | 28 | |
| Індекс цін, країна Л=1 | 1,5 | 2 | 3 | 2 | 4 | Середній індекс |
Обчислений таким чином середній індекс цін для товарної групи А'является приватним ППСВ. На його основі визначають ППСВ для аналітичних груп і компонентів ВВП. Для цього використовуються традиційні формули Пааше і Ласпейреса:
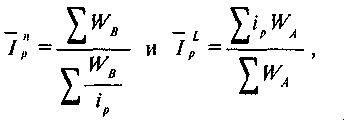
де ip - індекс цін i-го товару в країні В по відношенню до країни А;
I? Np - індекс Пааше;
I? Lp - індекс Ласпейреса;
WA - частка окремих товарних груп у ВВП країни А;
WB - частка окремих товарних груп у ВВП країни В.
Таким чином, в результаті цього розрахунку можна визначити два середніх індексу цін країн АН В, або дві величини ППСВ. Одна величина виходить, коли для зважування індексів цін, обчислених для окремих товарних груп, використовуються дані про структуру ВВП країни А, а інша - коли використовуються дані про структуру ВВП країни В.
Приклад. Припустимо, що ВВП країн A і B складається з п'яти товарних груп і що для кожної товарної групи визначені середні індекси цін. Дані для цього прикладу наведено в таблиці.
| Група товарів | Структура ВВП країни А |
Структура ВВП країни В |
Індекс цін, країна В=1 |
| 1 | 10,0 | 30,0 | 2,0 |
| 2 | 20,0 | 15,0 | 1,5 |
| 3 | 15,0 | 5,0 | 3,0 |
| 4 | 25,0 | 10,0 | 4,0 |
| 5 | 30,0 | 40,0 | 4, 5 |
| Разом | 100,0 | 100,0 | - |
Таким чином, середній індекс цін складе:
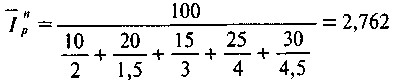
або
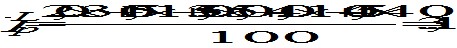
Для практичних цілей, однак, незручно мати два результати розрахунку, які самі по собі правомірні і теоретично виправдані, і тому для отримання тільки одного значення індексу застосовують формулу середньої геометричної, тобто індекс цін Фішера:
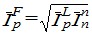
. (9.1)
Розділивши індекс вартості ВВП на індекс цін Фішера, одержимо шуканий результат, тобто співвідношення фізичних об'ємом ВВП двох країн А і В:

де ВВП - ВВП країни А у власній національній валюті;
ВВП - ВВП країни В у власній національній валюті;
I? q - індекс фізичного обсягу ВВП;
I? Fp - індекс цін Фішера.
Цей же результат може бути отриманий іншим способом. Так, якщо застосувати індекс цін для окремих товарних груп, можна обчислити ВВП країни А в цінах країни В, а ВВП країни В в цінах країни А. У цьому випадку спочатку визначаються два індексу фізичного обсягу для даної пари країн:
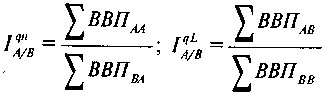
Потім обчислюється середній індекс фізичного обсягу на основі цих двох індексів за формулою Фішера. Він буде ідентичний індексу, отриманому за формулою (9.2).
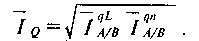
Як було зазначено вище, індекси, обчислені за формулою Ласпі-Реса, бувають, як правило, відносно більше, ніж індекси, обчислені за формулою Пааше. Цей феномен відомий як ефект Гершен-крона (по імені американського вченого Гершенкрона, який описав цю закономірність). Ставлення до ефекту Гершенкрона фахівців у галузі міжнародних зіставлень неоднаково. Одні з них вважають, що ефект Гершенкрона слід усунути з результатів розрахунків, оскільки він вносить певне викривлення. Вони пропонують використовувати такі формули індексів, які усувають ефект Гершенкрона, наприклад, формулу Фішера.
Інші фахівці, навпаки, вважають, що ефект Гершенкрона відображає природну економічну природу речей і що формули індексів, використовувані для зіставлень, не повинні усувати цей ефект. Вони пропонують для зіставлень використовувати середні міжнародні ціни, на які різні країни роблять різний вплив (залежно, наприклад, від їх розміру).
Найбільш важливим етапом розрахунку є підбір ідентичних товарів з цінами, заснований на двох основних принципах:
репрезентативність товарів, тобто їх характерність для структури витрат у даній країні ;
порівнянність товарів з товаром-представником країни партнера.
У ряді випадків важко досягти суміщення цих двох принципів, оскільки репрезентативні товари часто непорівнянні, а зіставні товари - нехарактерні для структури витрат у даній країні. Тому на практиці доводиться вдаватися до різних компромісів. Якщо товари непорівнянні за якісними характеристиками, вносяться поправки до цін на відмінності в якості. У деяких випадках процедура внесення таких поправок нескладна. Наприклад, якщо зіставляються ціни за 1 т залізної руди, вміст заліза в якій в країні А становить 3%, а в країні В-6%, то для приведення цін до порівнянного вигляду необхідно ціну в країні, 6 розділити на два. В іншому випадку при зіставленні національних цін на руду з різним вмістом заліза може створитися невірне уявлення про реальне співвідношення цін по цій групі товарів. Можливості застосування такого роду методу простих поправок до цін на товари, на жаль, дуже обмежені. Для більш складних товарів, таких, як автомашини, телевізори, холодильники і т. д., при внесенні поправок до цін з метою усунення відмінностей у цінах на товари використовуються методи регресійного аналізу. Ці методи передбачають складання регресійних рівнянь, в яких встановлюються складні зв'язки між найбільш важливими параметрами товарів та їх цінами. Наприклад, у випадку з автомобілями рівняння регресії встановлює зв'язок між ціною автомобіля і такими його параметрами, як потужність мотора, споживання бензину на 100 км пробігу, габарити, комфортабельність і ін У спеціальній літературі цей метод отримав назву гедонических індексів.
У багатьох випадках, однак, поправки до ціни товарів-представників вносяться на основі консультацій між експертами, добре знайомими з техніко-економічними параметрами.
При підборі аналогічних товарів-представників з цінами слід підготувати детальний опис товарів для ідентифікації товарів-представників на внутрішньому ринку. Опис товарів-представників має включати такі елементи:
код і найменування товарів;
загальний опис товару (марка, модель, місце виготовлення і т. д.);
технічні параметри (розмір, вага, об'єм, потужність, матеріал виготовлення і т. д.);
вказівку цільового призначення товару (сфера його застосування);
малюнок.
Головними джерелами інформації при визначенні цін на товари-представники, як правило, є:
дані розрахунку національного індексу споживчих цін (ІСЦ), а також розрахунку індексу оптових цін і т. д.;
спеціальні обстеження цін (наприклад, в багатьох країнах дані про ціни на товари виробничого призначення збираються від виробників, торгових компаній і т. д.);
каталоги;
прейскуранти.
Для оцінки товарів-представників використовуються середні ціни для економіки в цілому, що сприяє досягненню відповідності між обчислюваними індексами цін і оцінками ВВП за методами, прийнятими в СНР. У тих випадках, коли один і той же товар реалізується населенню через різні канали за різними цінами, для оцінки товарів-представників обчислюється середня ціна, зважена за обсягами товарів, реалізованих по відповідних каналах. У спеціальній літературі такий метод отримав назву принципу «картопля - це картопля». Цей принцип означає, що при обчисленні індексів, що характеризують співвідношення між цінами двох країн на той чи інший товар, не беруться до уваги відмінності в рівнях торгово-транспортних націнок різних країн.
Приклад. Припустимо, що в країнах А і В товар ^ реалізується по 5 каналах і що існує деяка диференціація в рівнях цін. Умови цього прикладу систематизовані в наступній таблиці:
| Канали надходження продукції | Країна А | Країна В | Індекс цін А / В (B=1) | ||||
| QA | РА | QAPA | QB | PB | QBPB | ||
| 1 | 20 | 2 | 40 | 30 | 1,0 | 30 | 2,0 |
| 2 | 10 | 4 | 40 | 20 | 2,0 | 40 | 1,6 |
| 3 | 40 | 3 | 120 | 40 | 2,0 | 80 | 1,5 |
| 4 | 15 | 5 | 75 | 5 | 2,0 | 10 | 2,5 |
| 5 | 15 | 6 | 90 | 5 | 3,0 | 15 | 2,0 |
| Разом | 100 | 3,7 | 365 | 100 | 1,75 | 175 | 1,9 |
З таблиці випливає, що середній індекс цін у двох країнах може бути обчислений двома методами: або як співвідношення середніх цін для всіх каналів (Ip=3,7 / 1, 85=2,0), або шляхом усереднення співвідношень цін для окремих каналів реалізації. Якщо в даному прикладі застосувати формулу середньої геометричної, то отримаємо:
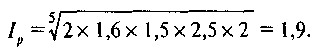
На практиці віддається перевагу першому методу, який відповідає згаданому вище принципом «картопля - це картопля». Однак критики цього методу відзначають, що він грунтується на необгрунтованому абстрагуванні від відмінностей у рівні торгово-транспортних витрат. Вони пропонують для обчислення індексу цін використовувати метод усереднення індексів цін, спочатку обчислених для окремих каналів реалізації товарів.
Описана вище процедура розрахунків використовується в так званих прямих парових (двосторонніх) порівняннях ВВП на основі ППСВ, тобто в порівняннях, проведених безпосередньо для тієї чи іншої пари країн. У теорії міжнародних зіставлень прийнято розрізняти прямі парні і багатосторонні зіставлення, які здійснюються одночасно для деякої групи країн. Міжнародні економічні організації (ООН, ОЕСР, Світовий банк і т. д.), як правило, проводять багатосторонні зіставлення. Методологія міжнародних багатосторонніх зіставлень має свою специфіку. Перш ніж ознайомитися з нею, видається доцільним розглянути основні вимоги до індексів, використовуваним в міжнародних порівняннях.
Основними вимогами, представленими у вигляді деяких логічно виведених постулатів, є:
вимога характерності ваг, згідно з яким при обчисленні, індексів для зважування індексованих величин повинні бути застосовані ваги, характерні для економіки зіставляються країн. Так, при зіставленні ВВП США і Росії в якості ваг необхідно використовувати ціни або США, або Росії, або середні ціни США та Росії, але не ціни небудь інший третьої країни;
вимога транзитивності, тобто результат, отриманий шляхом прямого парного зіставлення показників двох країн (А і В), повинен бути дорівнює індексу, виражає співвідношення між показниками цих двох країн, але исчисленному непрямим чином через третю країну, що виконує роль посередника («перехідного моста »). Наприклад, якщо в зіставленні беруть участь три країни А, В і D, то індекс зіставлення показників країн А і зможе бути отриманий за допомогою прямого зіставлення показників країн А і В, але також шляхом ділення індексу IA / D на індекс IB / D. Іншими словами, вимога транзитивності може бути записано таким чином:
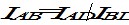
,
де 1А / В - індекс прямого зіставлення показників країн А і В;
1А / D - індекс прямого зіставлення показників країн А і D,
IB / D - індекс прямого зіставлення показників країн В і D.
Вимога транзитивності дуже важливо для багатосторонніх зіставлень, оскільки індекси, обчислені для деякої групи країн, повинні бути строго взаємно узгоджені і не давати суперечливих відповідей;
вимога незалежності індексу від вибору базисної країни. Це інша важлива вимога до індексів як прямих парових (двосторонніх), так і багатосторонніх зіставлень. Сенс його полягає в тому, що величина індексів не повинна залежати від вибору базисної країни. Математично це вимога можна записати наступним чином:
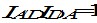
.
Ця вимога припускає, що твір індексу, що виражає співвідношення показників країни А до країни D, та індексу, що виражає співвідношення показників країни D до країни А, має дорівнювати 1;
вимога адитивності, тобто індекси, отримані для окремих компонентів ВВП, повинні бути узгоджені між собою і з індексом ВВП в цілому. Наприклад, не повинно бути такого положення, при якому індекс споживання країни А до країни В дорівнює 110, індекс накопичення - 115, а індекс ВВП - 120.
Вимога аддитивности припускає, що показник ВВП країни А в цінах країни В може бути отриманий шляхом підсумовування окремих елементів ВВП країни А в цінах країни В.
Необхідно відзначити, що не всі методи і формули індексів відповідають вимогам адитивності. Слід також мати на увазі, що деякі згадані вище вимоги до індексів знаходяться у відомому протиріччі один до одного. Зокрема, вимога характерності ваг суперечить вимозі транзитивності, оскільки індекси, які найбільшою мірою відповідають вимозі характерності ваг, як правило, нетранзитивну. Наприклад, формула індексу Фішера, відповідна вимогу характерності ваг і дозволяє отримати однозначну результат для кожної пари країн, не задовольняє вимогу транзитивності.
Перейдемо тепер до розгляду методів багатосторонніх зіставлень, індекси яких повинні відповідати згаданим вище вимогам.
Особливість багатосторонніх зіставлень полягає не тільки в тому, що вони проводяться для групи країн, а й у тому, що інформація про ціни і кількості виробленої та використаної в цих країнах продукції розглядається і обробляється як єдине ціле для отримання системи взаємопов'язаних індексів, що відповідають ряду вимог аналітичного характеру.
Якщо, наприклад, зіставлення проводиться для групи країн А, В, С, D і Е і показники цих країн порівнюються один з одним на основі методології парних зіставлень, тоді можна отримати ряд індексів Фішера для кожної пари країн: А і В, С і D і т. д. Такі розрахунки не можна розглядати як справді багатосторонні зіставлення, а їх результати можуть бути взаємно суперечливі. Наприклад, в результаті зіставлень може виявитися, що
А> В, В> С, С> D, a D> А. Така можливість теоретично існує, так як в даному випадку застосовується метод прямих парних зіставлень, в результаті яких виходять індекси Фішера, які, однак, нетранзитивну. Транзитивність індексів може бути забезпечена, якщо застосовується метод багатосторонніх зіставлень. Одним з таких методів багатосторонніх зіставлень, який в даний час широко застосовується на практиці, є метод екш (екш - це великі літери прізвищ трьох статистиків, що запропонували цей метод: угорців Елтете і Кевеша і поляка Шульца). Формула індексу екш для країн А і В має наступний вигляд:
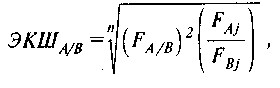
де FA / B - індекс Фішера для країн А і В;
FAj - індекс Фішера для країн А і J;
РBj - індекс Фішера для країн B і J;
п - число країн, що беруть участь в зіставленні;
j=A, B, C, ... j.
На основі формули екш можна отримати індекси, відповідні вимогу транзитивності і лише в найменшій мірі відступаючі від вимоги характерності ваг. Зауважимо, що у формулі екш індекс Фішера для даної пари країн (А і В) має вагу 2. Крім того, враховуються також індекси Фішера, отримані для даної пари країн непрямим шляхом, тобто через країну-посередника. Наприклад, індекс країни А до країни зможе бути отриманий шляхом ділення індексу Фішера А / С на індекс Фішера В / С. Таким чином, індекс екш для країн А і В - це середній індекс з усіх обчислених прямо і побічно індексів Фішера для країн А і В. При цьому, як зазначено вище, індекс Фішера, отриманий на основі прямого парного зіставлення, береться вагою, що дорівнює 2. Наприклад, якщо в зіставленні беруть участь чотири країни: А, В, Сі D, то індекси екш будуть мати наступний вигляд:




Індекси екш відповідають вимозі транзитивності і незалежності від вибору країни, однак вони не відповідають вимозі адитивності, і це є їх істотним недоліком.
Приклад. Розрахуємо екш, використовуючи вихідні дані, наведені в таблиці.
| Країни | Ціни товарів-представників | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| А | 2 | 6 | - | - | 10 | _ | 1 | 4 |
| В | 12 | 35 | 3 | 5 | 40 | - | - | 18 |
| С | 25 | 50 | 7 | 12 | - | 10 | - | - |
| D | 150 | 400 | - | 100 | - | 70 | 80 | - |
| Співвідношення цін на товаpом-представники | ||||||||
| В / А | 6,0 | 5,83 | - | - | 4,0 | - | _ | 4,5 |
| С / А | 12,5 | 8,33 | - | - | - | - | - | - |
| D / A | 75,0 | 66,67 | - | - | - | - | 8,0 | - |
| С / В | 2,08 | 1,42 | 2,3 | 2,4 | - | - | - | - |
| D / В | 12,5 | 11,42 | - | 20,0 | - | - | - | - |
| D / С | 6,0 | 8,0 | - | 8,3 | - | 7,0 | - | - |
Визначимо середні індекси для кожної пари країн за формулою середньої геометричної:

D / A=73,681; С / B=2,021; D / B=12,182; D / С=7,274.
Однак отримані індекси нетранзитивну. Так, індекс, отриманий на основі прямого зіставлення показників країн В і А, не дорівнює індексу, отриманому непрямим шляхом через показники країни-посередника С:
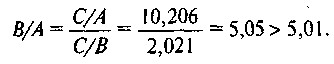
Але, як було зазначено вище, вимогу транзитивності відповідають індекси, які обчислюються за формулою екш. Наприклад, індекс екш для країн А і В на основі наведених вище даних може бути обчислений наступним чином:
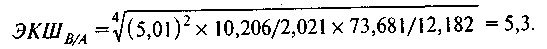
Іншим методом зіставлення, широко застосовуваним на практиці міжнародними організаціями, є метод Гирі-Каміса. Формула індексу Гирі-Каміса має наступний вигляд:
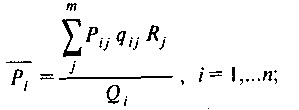
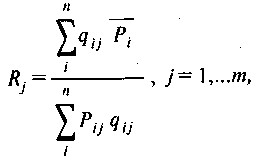
де Rj - паритет купівельної спроможності валют j-ї країни стосовно валюти базисної країни;
P? I - середня міжнародна ціна г-го товару;
Рij - ціна i-го товару в j-й країні;
qij - кількість i-го товару в j-й країні;
Qi - загальна кількість i-го товару у всіх країнах;
п - число товарів;
т - число країн.
Таким чином, за допомогою методу Гирі-Каміса можна вирішити сис-темулінейнихуравненій і одночасно визначити ППСВ (/?.) І середні міжнародні ціни (Р.). Оцінка показників всіх країн у міжнародних цінах дозволяє отримати індекси, які транзитивні, адитивні і не залежать від вибору базисної країни. Однак індекси Гирі-Каміса не відповідають вимогу характерності ваг.
Існують і інші методи багатосторонніх зіставлень. Наприклад, в спеціальній літературі описаний метод Уолша. Його формула має наступний вигляд:
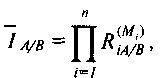
де RiA / B - паритет купівельної спроможності валют для i-й товарної групи (обчислений як середня геометрична невиважена з співвідношень цін на товари-представники країн А і В);
Мi - частка товарної групи в загальному агрегаті, наприклад у ВВП; визначається як середня частка цієї товарної групи в усіх країнах, що приймають участь у зіставленні. Наприклад, якщо частка витрат на м'ясні продукти в країнах А, В і С становить 5, 6 і 7,; тоді М для даної товарної групи дорівнює 6.
Приклад. Припустимо, що в зіставленні беруть участь три країни А, В, Сі що ВВП всіх країн складається з трьох груп товарів. Дані про індекси ППСВ цих груп товарів та їх питомих вагах представлені в таблиці:
| Групи товарів | Структура країни А | Структура країни У | Структура країни З | Індекси цін (А / В) | Індекси цін (С / В) | Середня структура |
| 1 | 20,0 | 40,0 | 60,0 | 1,5 | 4,0 | 40,0 |
| 2 | 30,0 | 40,0 | 20,0 | 2,0 | 6,0 | 30,0 |
| 3 | 50,0 | 20,0 | 20,0 | 3,0 | 5,0 | 30,0 |
| Разом | 100,0 | 100,0 | 100,0 | - | - | 100,0 |
Для здобуття середньої індексу цін (ППСВ) країн А, В і С на основі формули Уолша проведемо наступні обчислення:
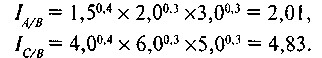
Індекси Уолша транзитивні, і в цьому їх безумовне гідність. Вони відповідають вимозі незалежності індексу від вибору базис-Ной країни, але не відповідають вимозі адитивності.
Інший метод багатосторонніх міжнародних зіставлень - метод Джірарді - заснований на використанні середніх міжнародних цін, що обчислюються виходячи з середніх національних цін за допомогою формули середньої геометричної невиваженою. Індекси, одержувані на основі цього методу, відповідають вимогам транзитивності, аддитивности та незалежності від вибору базисної країни. При застосуванні формули Джірарді «ефект Гершенкрона» не робить впливу на результати зіставлення. Однак економічний зміст середніх міжнародних цін, що обчислюються за формулою Джірарді, неясно. Проте формула Джірарді застосовувалася недовгий час у міжнародних порівняннях ВВП на основі ППСВ, що проводяться для європейських країн відділом статистики Європейського Співтовариства (Євростатом).
У деяких випадках для багатосторонніх зіставлень застосовується метод центральної країни. У відповідності з цим методом показники ВВП всіх країн порівнюються з ВВП однієї країни, що розглядається в якості базисної (центральної) країни. У цьому випадку індекси для будь-якої пари країн (крім тих пар країн, однією з яких не є центральна країна) обчислюються непрямим методом, тобто шляхом зіставлення індексів показників цих країн до показників центральної країни. Наприклад, якщо в зіставленні беруть участь чотири країни А, В, Сі D, а в якості центральної розглядається країна А, тоді індекс, що характеризує співвідношення показників країн і і С, обчислюється таким чином: 1В / С=1В / А / 1С / А .
Індекси, одержувані таким методом, транзитивні, однак транзитивність досягається певною мірою механічним шляхом. Це означає, що індекс IB / C, обчислений вищеописаним непрямим методом, буде відрізнятися від індексу IB / C, обчисленого на основі прямого парного зіставлення країн В і С. Крім того, індекси, обчислені за допомогою методу центральної країни, що не відповідають вимозі незалежності від вибору центральної країни. Це означає, що якби в якості центральної країни була обрана країна D, а не країна A, тоді співвідношення між показниками всіх країн були б іншими. Тому метод центральної країни, хоча і широко застосовується на практиці в міжнародних порівняннях, не розглядається як повноцінний метод багатосторонніх зіставлень. Його застосування пов'язане головним чином з міркуваннями практичного характеру: відсутність вичерпної інформації, економія ресурсів і т. д.
Інформація, релевантна "§ 1. ЗАГАЛЬНІ ПРИНЦИПИ МЕТОДОЛОГІЇ"
- РЕКОМЕНДОВАНА ЛІТЕРАТУРА
Блауг М. Економічна думка в репроспектіве. М., 1995. Гол. 17. Фрідмен М. Методологія позитивної економічної науки / / ТНЕ815. 1994. Вип. 4. Блауг М. Нескладний урок економічної методології / / ТНЕ818. 1994. Вип. 4. Хаусман Д. Економічна методологія в двох словах / / Світова економіка і міжнародні відносини. 1994. № 2, 3. КейнсДж.Н. Предмет і метод політичної економії (1891): - Рекомендована література
Блауг М. Економічна думка в репроспектіве. М., 1995. Гол. 17. Фрідмен М. Методологія позитивної економічної науки / / THESIS. 1994. Вип. 4. Блауг М. Нескладний урок економічної методології / / THESIS. 1994. Вип. 4. Хаусман Д. Економічна методологія в двох словах / / Світова економіка і міжнародні відносини. 1994. № 2, 3, КейнсДж.Н. Предмет і метод політичної економії (1891): - 5.1. Три мотиву написання цієї глави
Перший. Йде процес інтенсивного освоєння системно-комплексний методології у вирішенні проблем якості. Спостерігається інтернаціоналізація досвіду управління якістю продукції, яка відкриває нові грані і межі застосовуваної методології. Інтернаціоналізація досвіду управління якістю показує, що ми маємо справу з новим процесом, з новим явищем, для якого характерні загальні риси і - Глава 41 Кілька слів про методологію
Глава 41 Кілька слів про - Методологія здійснення високій ймовірності коротких продажів
Існує дві стратегії короткого продажу акції з високою імовірністю успіху. Перша - знаходження вкрай перекуплених ак-цій. Друга стратегія - пошук паперів, що вступають у тривалістю-ний ведмежий тренд або знаходяться в ньому. Обидві методології включають в себе процес фільтрації. Успішний короткостроковий трейдинг звичайно заснований на довгостроковому аналізі. Коли ви шукай-ті акції для короткої - Посвячення
Присвячується пам'яті професора, доктора технічних наук Василя Васильовича Бойцова основоположника системно-комплексний методології вирішення великих організаційно-технічних завдань. А. В. - Розділ I ЗАГАЛЬНІ ОСНОВИ ЕКОНОМІКИ
У розділі I розглядається цільова функція економічної діяльності людей, проблема рідкості, загальні закономірності економічної організації суспільства, проблеми власності як найважливішої характеристики економічної системи, аналізуються основні риси ринкової економіки, місце і роль держави в господарському житті суспільства, особливості сучасної російської економіки. - 2. Монографії
Антологія економічної класики: У 2-х т. М., 1993. Антонов Н., Пессель М. Грошовий обіг, кредит і банки. М., 1995. Арістер Н., Половінкін П., Сахарнов Ю. Підприємництво як стратегічний фактор економічного розвитку. СПб., 1996. Бабич A.M. та ін Соціальна сфера в умовах переходу до ринку. М., 1993. Браунінг П. Сучасні економічні теорії. М., 1987. Бункина М.К. - Вчіться мислити, філософствувати
! Якщо хочете оволодіти могутністю філософствування, в т.ч. діалектичної логіки, навчитися застосовувати логіку і діалектику як прямого, безпосереднього, загальнонаукового, свідомого, практичного, спостережуваного методу пізнання, мислення, дослідження, творчості, то Вам у цьому допоможуть «Самовчитель мислення» та «Філософія» навчальний посібник автора для аспірантів [см .20; 24] Усвідомлюючи - 9. АМЕРИКАНСЬКИЙ інституціоналізму
Основоположник інституціоналізму Т. Веблен. Робота Т. Веблена «Теорія дозвільного класу». Інституціоналізм: предмет дослідження, методологія. Дж. Коммонс і його погляди. У. Мітчелл про теорію циклів. Критика неокласиків. Вплив інституціоналізму на розвиток економічної - § 1. ЗАГАЛЬНІ ПРИНЦИПИ
Обчислення показників продукції галузей економіки, які використовуються в СНР при обчисленні ВВП, грунтується на наступних принципах: при обчисленні показників продукції галузі визначається одиниця класифікації, що описує економічні одиниці, з яких складається галузь; одиницею класифікації згідно з Міжнародною стандартною галузевою класифікацією всіх видів економічної - Питання для повторення
1. Назвіть загальні економічні умови, що підготували перехід до рабовласницького спо-собу виробництва, 2. Назвіть загальні закономірності економічного розвитку країн Стародавнього Сходу? 3. У чому суть давньоєгипетської системи освоєння сільськогосподарських угідь? 4. Охарактеризуйте господарство Стародавньої Греції після об'єднання полісів? 5. Охарактеризуйте господарство Стародавнього Риму в період його - Розробити план дій
Отже, ви знаєте, що вами зроблено, що ви хочете зробити і чого прагнете досягти. Тепер перейдемо до деталей. Інформацію, излагаемую в цій книзі, вам належить застосувати на практиці. Ось два основних пункти вашого плану: методологія торгівлі та управління торговим - 1. ЩО ТАКЕ МЕТОДОЛОГІЯ І ЧИМ викликати інтерес ДО НЕЇ СЬОГОДНІ?
У найзагальнішому сенсі методологія - спосіб, яким установляется відношення між теорією і реальністю. Вона впливає на вибір питань, які визнана вирішувати теорія, на їх ієрархію, інтерпретацію пропонованих рішень, охоплює принципи, регулярно застосовуються при формулюванні та обгрунтуванні економічних теорій. «Методологія об'єднує як методи, які зазвичай використовуються якоїсь школою - 1. Що таке методологія і чим викликаний інтерес до неї сьогодні?
У найзагальнішому сенсі методологія - спосіб, яким установ-ляется відношення між теорією і реальністю. Вона впливає на вибір питань, які визнана вирішувати теорія, на їх ієрархію, інтерпретацію пропонованих рішень ', охоплює принципи, регулярно застосовуються при формулюванні та обгрунтуванні економічних теорій2. «Методологія об'єднує як методи, які зазвичай використовуються якоїсь школою