| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Розглянутий вище аналіз ринкової рівноваги стосувався головним чином статичного стану системи. Звернемося тепер до дослідження механізму досягнення рівноваги, т. Е. До динаміки процесу.
Припустимо для простоти, що попит і пропозиція представлені лінійними функціями. Введемо параметр часу. Нехай величина попиту (обсяг покупок) безпосередньо реагує на поточну ринкову ціну, а обсяг пропозиції змінюється під впливом ціни з деяким запізненням. Такий вибір динаміки попиту і пропозиції легко пояснити на основі емпіричних спостережень. Споживач швидше пристосовується до поточного стану справ на відміну від виробника, який зможе відреагувати на поточну ринкову ситуацію тільки в наступному періоді часу, коли закінчиться наступний цикл виробництва і продавець знову вийде на ринок.
Тоді динамічна функція попиту буде дорівнює: Q? = А-ЬРг
Динамічна функція пропозиції складе: Qst = C + dPt_1.
причому а > сіЬ > 0, d > 0.
У рівновазі величина попиту дорівнює величині пропозиції: Qf = Qst. Тому отримуємо наступне рекурентне вираз, що характеризує динаміку ринкової ціни:
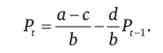
Знайдемо ряд цін. Якщо ціна початку відліку (нульового періоду) дорівнює Р0, то ціна першого періоду часу буде дорівнювати
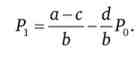
Ціна другого періоду дорівнюватиме
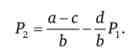
Але в вираженні для ціни другого періоду ми можемо замінити ціну першого періоду її співвідношенням з базовою ціною (ціною нульового періоду):
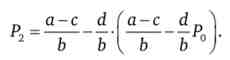
Подібним чином ми можемо послідовно підставляти ціну попереднього в ціну наступного періоду. Тоді для ціни періоду t отримаємо такий вираз:
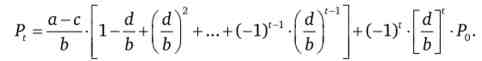
а-з Г d (dV fdY '1
Перший доданок тут --- 1 + - +...+(-1) - - - перед-
ь I видання {bj? j
- " а-з
ставлять собою геометричну прогресію з першим членом-й зна
d b
менателем -. Сума даної геометричній прогресії знаходиться як:
ь
1-С-1У - -
d ~~ з 4 J і
S =---т-2. І ціна в період t буде дорівнює
ред
ред
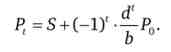
Коли на ринку встановлюється рівноважна ціна, це означає, що ціни двох періодів t і t - 1 рівні між собою. Позначимо рівноважну ціну Р Тоді довільну ціну в будь-який період часу можна, використовуючи отриману вище формулу, висловити через базову ціну Р0 і рівноважну ціну Р ":
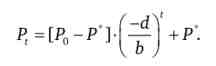
Тепер ми можемо повністю проаналізувати динаміку ринкових
цін' d (d
якщо 0 < - < 1, то вираз I - I прагне до нуля зі збільшенням р
Сума геометричній прогресії має кінцевий межа. Ціновий ряд сходиться до рівноважної ціною. Амплітуда коливань цін зменшується з кожним періодом, поки не буде досягнута рівноважна ціна. Ця рівновага виявиться стійким (стабільним). Динаміка цін на такому ринку представлена на рис. 3.14, а.
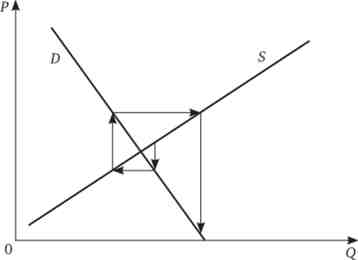
При відхиленні поточної ціни від рівноважної на такому ринку ціна прагне повернутися до рівноважного рівня шляхом ряду взаємодій між попитом і пропозицією. Цей механізм, зображений графічно, нагадує павутину (рис. 3.15). Звідси зрозуміло, чому дана модель отримала назву «паутинообразная модель ринку».
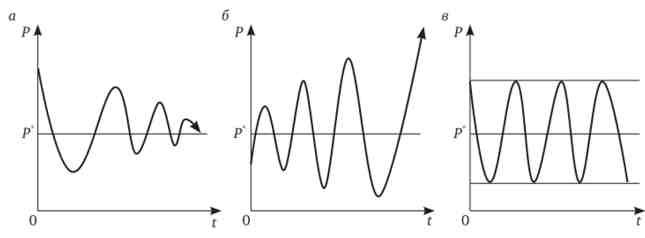
Мал. 3.14. Динаміка ринкової ціни
Мал. 3.15. Сталий рівновагу на ринку в паутинообразной моделі
якщо - > 1, то сума геометричної прогресії прагне до бесконеч- b
ності, цінової ряд розходиться. Коливання цін посилюються з часом. Один раз відхилившись від рівноважної ціни, поточна ціна ніколи не повернеться до рівноваги. Рівновага виявиться нестійким (нестабільним). Павутина цін почне розкручуватися. Динаміка цін зображена графічно на рис. 3.14, б і 3.16.
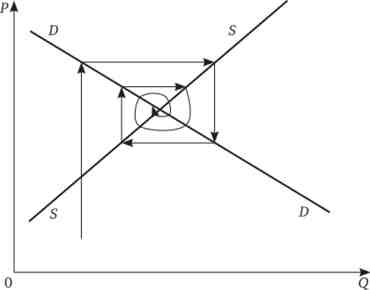
Мал. 3.16. Нестійка рівновага на ринку в паутинообразной моделі
Якщо т-= 1, то на ринку відбуватимуться коливання з постійною b
амплітудою. Рівновага також виявиться нестійким, але ця нестійкість носить локальний характер, ціна рухається по замкнутому контуру. Подібна динаміка ціни зображена графічно на рис. 3.14, в. Ми також бачили її і раніше на рис. 3.8, б.
Питання для суперпрофесіоналів
Чи можна, використовуючи паутинообразная модель (і (або) її необхідні модифікації) обгрунтувати стійкість і нестійкість рівноваги по Вальраса і по Маршаллу? (Див. Вставку вище.)