3.8 Індекси цін і реального доходу
Нас часто цікавлять зміни у вартості життя у зв'язку із змінами доходів і (або) цін.
Припустимо, що витрати споживача дорівнюють його доходам і складають в початковому (базисному) періоді:
I0=? Q0p0
а в поточному:
It=? qtpt
Тут верхній індекс 0 відповідає показникам базисного, а індекс t - поточного періоду; q і р - відповідно кількості товарів, що купуються і їх ціни , індекси товарів опущені, оскільки знак? увазі суму витрат на придбання усього безлічі товарів (споживчого кошика).
Для оцінки зміни вартості життя в поточному періоді в порівнянні з базисним слід визначити індекси номінального доходу і цін.
Індекс номінального доходу визначити легко, він складе:
MI=It/I0 (3.19)
Індекс цін може бути визначений двома способами: як індекс Ласпейреса:
PL=? q0pt /? q0p0 (3.20)
і як індекс Паші:
PP=? qtpt /? qtp0 (3.21)
названі так по імені німецьких статистиків Е. Ласпейреса (1834-1913) і Г. Пааше (1851-1925). [1]
Індекс Ласпейреса передбачає зважування цін двох періодів за обсягами споживання товарів у базисному, а індекс Пааше - за обсягами їх споживання в поточному періоді.
Проте ні той ні інший індекс не дають вірного уявлення про зміну цін, оскільки вони не враховують впливу цієї зміни на структуру споживання.
Очевидно, що якщо (у звичайній двухпродуктовой моделі) ціна товару X зростає (PtX> P0X), то покупки його знижуються (qtX
Можна показати, що положення споживача в поточному періоді буде краще, ніж у базисному, якщо індекс Ласпейреса виявиться нижче індексу номінального доходу:
It/I0>=PL (3.22)
Можна показати також, що положення споживача в поточному періоді буде гірше, ніж у базисному, якщо індекс Пааше виявиться вище індексу номінального доходу:
It/I0 <=PP (3.23)
Розглянемо спочатку індекс Ласпейреса. Якщо? Q0pt? It, початковий набір товарів (вектор q0), очевидно, доступний споживачу і при поточних цінах (вектор pt) і доході It.
Значить, і в умовах, що змінилися споживач міг би і раніше купувати початковий набір q0.
Якщо ж фактично в поточному періоді він купує інший набір (вектор qt), то або:
? Q0pt це означало б, що набір qt належить більш високою кривої байдужості, тобто обіцяє споживачеві більше задоволення, ніж набір q0, або:
? q0pt=? qtpt, (3.24 *)
це означало б, що набори q0 і qt мають рівну вартість, тобто належать одній і тій же бюджетної прямій, але споживач явно віддає перевагу набір qt, який обіцяє йому більше задоволення, тобто належить більш високою кривої байдужості.
Розділивши обидві частини (3.24) на? Q0p0, маємо:
? Q0pt /? Q0p0=? Qtpt /? Q0p0 (3.25)
Ліва частина (3.25) являє індекс цін Ласпейреса, права - індекс номінального доходу. Отже: PL
На рис. 3.27 первісний доход і ціни товарів представлені бюджетної прямої I0I0:
I0=? Q0p0=q0Xp0X + q0Yq0Y (3.26)
дохід і ціни поточного періоду - бюджетної прямої ItIt:
It=? qtpt=qtXptX + qtYptY (3.27)
Первісному оптимуму споживача відповідає точка А (q0X, q0Y), поточним - точка В (qtXx, qtY) :
Нова бюджетна пряма ItIt, як і первісна I0I0, проходить через точку А, що свідчить про доступність для споживача колишнього оптимального набору А в умовах, що змінилися.
Тепер розглянемо індекс Пааше. Якщо? Q0p0>? Qtp0, набір qt, обираний в період t, був доступний споживачеві і в період 0. І якщо тоді він вважав за краще все ж набір q0, то лише тому, що останній обіцяв йому більше задоволення, належав до більш високої кривої байдужості.
Розділивши обидві частини нерівності на? Qtpt отримаємо:
? Q0p0 /? Qtpt>? Qtp0 /? Qtpt (3.28)
або, інакше:
? qtpt /? q0p0 Ліва частина (3.29) являє індекс номінального доходу, права - індекс цін Пааше.
Отже: PP &gr; MI
Таким чином, твердження (3.23) також доведено.
Цей висновок ілюструє рис. 3.28, подібний рис. 3.27. Тут оптимум споживача при I0, p0, опинився в точці С (q0X, q0Y)-Хоча набір D (qtX, qtY) лежить на тій же бюджетної прямої I0I0, споживач в початковий період волів набір С, оскільки він лежить на вищій кривій байдужості .
Після зміни цін бюджетна пряма зайняла положення ItIt:
It=? (Qtpt)=qtXptX + qtYptY (3.30)
Вона проходить нижче первісного оптимуму С, який тепер недоступний для споживача. Отже, вибираючи набір qt, споживач знижує своє задоволення в порівнянні з початковим періодом.
Індекс реального доходу характеризує зміну купівельної спроможності номінального доходу. Якщо при розрахунку індексу цін ціни товарів зважуються за обсягами їх придбання у базисному або поточному періоді, то при розрахунку індексу реального доходу, навпаки, обсяги споживання кожного періоду зважуються за цінами базисного або поточного періоду. Індекс реального доходу Ласпейреса має вигляд:
RL=? P0qt /? P0q0 (3.31)
а індекс реального доходу Пааше відповідно: PP=? Ptqt /? Ptq0 (3.32)
Знаменник (3.31) являє номінальний дохід у період 0, або бюджетне обмеження:
I0=? p0q0 (3.33)
чисельник - дохід, необхідний для придбання в період t набору qt при цінах базисного періоду (p0). Чисельник (3.32) являє номінальний дохід у період t, або бюджетне обмеження: It=? Ptqt (3.34)
Використання індексів (3.31) і (3.32) приводить до одних і тих же результатів, якщо ціни залишаються незмінними (pt=p0), а змінюється лише номінальний дохід, або якщо при незмінному номінальному доході всі ціни змінюються в одному напрямку (ростуть або падають). Якщо ж змінюються ціни, результати розрахунків по (3.31) і (3.32) можуть виявитися різними. Нарешті, якщо обсяги споживання різних товарів змінюються в різному напрямку (споживання одних росте, інших падає), може статися так, що один індекс свідчитиме про зростання, а інший - про зниження реального доходу.
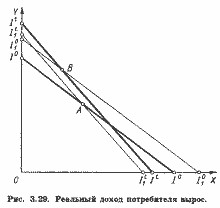
Розглянемо спочатку випадок, коли обидва індекси вказують на однакову спрямованість зміни реального доходу. На рис. 3.29 лінія I0I0 представляє бюджетне обмеження в період 0, коли споживач вибирає набір А. У період t ціна товару X підвищується і одночасно змінюється номінальний дохід споживача. Тепер він представлений бюджетної прямої ItIt, споживач вибирає набір В.
Нанесемо на графік індекси Ласпейреса і Пааше. Ми знаємо, що знаменник індексу Ласпейреса вже представлений на ньому бюджетною лінією I0I0. Його чисельник - грошовий дохід, необхідний для покупки набору В при цінах базисного періоду. Отже, ми можемо представити його на графіку допоміжної бюджетної прямої q01q01, що проходить через точку В і паралельної лінії q0q0. Оскільки графічне відображення чисельника індексу лежить вище відображення його знаменника, ми можемо укласти, що RL> 1 і, значить, реальний дохід споживача виріс.
Чисельник індексу Пааше відображений на графіку бюджетної прямої ItIt. Його знаменник, як ми пам'ятаємо, представляє номінальний дохід, необхідний для покупки набору А при цінах поточного періоду.
Таким чином, у ситуації, представленої на рис. 3.29, обидва індекси свідчать про те, що реальний дохід споживача виріс.
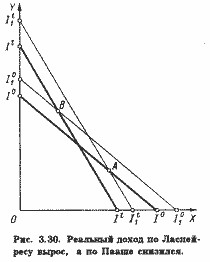
Розглянемо тепер ситуацію, коли індекси Ласпейреса і Пааше суперечать один одному.
На рис. 3.30 споживач вибирає набір А при бюджетному обмеженні I0I0 у базисному періоді і набір В при бюджетному обмеженні ItIt в поточному періоді. Лінії I01I01 і It1It1 представляють допоміжні бюджетні прямі, графічно відображають чисельник індексу Ласпейреса і відповідно знаменник індексу Пааше. З взаємного розташування ліній I0I0 і I01I01 і відповідно ItIt і It1It1 випливає, що RL> 0, але RP <0. Інакше кажучи, індекс Ласпейреса свідчить про зростання реального доходу, а індекс Пааше - про його зниження.
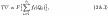
З рис. 3.30 ясно, що набір В був недоступний споживачеві у базисному періоді (при бюджеті I0I0), а набір А недоступний йому в поточному періоді (при бюджеті ItIt) - Однак ми не можемо зробити висновок про те, яку комбінацію товарів X і Y споживач вважає для себе переважніше-А або В, якщо у нас немає інформації про його карті байдужості. Можливо, що крива байдужості, що стосується бюджетної прямої в точці В, лежить вище тієї, що стосується іншої бюджетної прямої в точці А. Але можливо і зворотне.
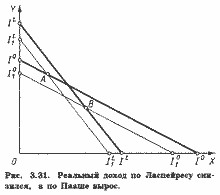
Розглянемо ще одну ситуацію. На рис. 3.31 представлений випадок, коли індекс Ласпейреса вказує на зниження реального доходу в поточному періоді, а індекс Пааше - на його зростання. Таке співвідношення індексів суперечить раніше зробленому висновку про те, що індекс Ласпейреса завжди більше індексу Пааше. Це можна пояснити тим, що, хоча в поточному періоді ціна товару X щодо виросла, проте обсяг покупок товару X також збільшився. Це, однак, суперечить аксіомам раціональної поведінки і можливо лише в тому випадку, якщо в період t смаки і переваги споживача змінилися. Але тоді індекс реального доходу вже не характеризує дійсного зміни реального доходу споживача.

Обчислення індексів реального доходу втрачає сенс і в тому випадку, якщо в одному (не обов'язково в базисному) періоді значна частина товарів розподіляється по картках, талонах (або спостерігається їх дефіцит), а в іншому (НЕ обов'язково поточному) - у порядку вільної торгівлі. Індекси доходу і цін пов'язані певним співвідношенням. Розділивши індекс номінального доходу (3.19) на індекс цін Пааше (3.21), ми отримаємо індекс доходу Ласпейреса (3.31):
MI / PP=)? Ptqt /? P0q0): (? Ptqt /? p0qt)=? p0qt /? p0q0? RL (3.35)
Відповідно розділивши індекс номінального доходу на індекс цін Ласпейреса (3.20), ми отримаємо індекс реального доходу Пааше (3.32):
MI / PL=) ? ptqt /? p0q0): (? ptq0 /? p0q0)=? ptqt /? ptq0? RP (3.36)
ПРИМІТКИ
[1] Однак, як зазначає Г. В. Ковалевський (Ковалевський Г. В. Індексний метод в економіці. М., 1989), першим "винахідником" агрегатного індексу цін з вагами поточного періоду був англійський економіст Томас Ман, який в 1609г. у роботі "Міркування про торгівлю Англії з Ост-Індією" (російський переклад см. в сб.: Меркантилізм. Л., 1935) обчислив такі індекси. У 1807г. вийшла книга російського економіста Федора Вирста "Міркування про деякі предмети законодавства і управління фінансами і комерцією Російської імперії ...", в якій був вперше обчислений агрегатний індекс цін з вагами базисного періоду. Таким чином, індекс Пааше й індекс Ласпейреса були вже відомі, але не були записані у формульному вигляді. І тільки з легкої руки американського економіста К. М. Уолша в 1874 р. індекси Мана і Вирста отримали імена Пааше і Ласпейреса.
Інформація, релевантна " 3.8 Індекси цін і реального доходу "
- Терміни і поняття
цін Індексація доходів« Діряве відро »А. Окуня Прожитковий мінімум (соціальний і фізіологічний) Крива Лоренца Квінтільний (доцільний) коефіцієнт Індекс концентрації доходів населення (коефіцієнт Джині) Мінімальний розмір оплати праці Соціальна справедливість Соціально орієнтована економіка Бідність Абсолютна межа бідності Відносна межа бідності Дефіцит - Ключові терміни
індекс потреби- чих цін (CPI) Номінальний валовий національний продукт (ВНП) Реальний валовий національний продукт 38 Поточні та постійні доллариДефлятор BH П Відносні і реальні цениПроцентние ізмененіяТемп пріростаТемп інфляцііВременной рядПространственная виборкаДіаграмма - 1.5. Макроекономічні показники рівня цін
індекси цін. Вони призначені для визначення середнього зміни цін в економіці. Всі індекси цін описують зміна вартості репрезентативного набору (кошика) товарів, зважене за кількістю кожного товару. Види індексів цін: - індекс оптових цін (на всі товари, що реалізуються великими партіями); - індекс цін виробників (оптових цін на товари окремих галузей); - індекс - Терміни і поняття
цін Ласпейраса Індекс цін Пааше Індекс Фішера Валовий випуск Чистий національний продукт (ЧНП) Транспортні платежі Непрямі податки Загальний особистий дохід Наявний доход населення Національне багатство Чистий економічний - 6. Як читати біржові індекси, котирування і рейтингові оцінки
індекси і котирування) залишається досить точним індикатором стану справ у - Класифікація доходів
індексу цін. Реальні доходи характеризують номінальні доходи з урахуванням зміни роздрібних цін (і тарифів). Реальні грошові доходи визначаються виходячи з грошових доходів поточного періоду за мінусом обов'язкових платежів і внесків, скоригованих на індекс споживчих цін. Заробітна плата - це ціна трудових послуг, що надаються найманими працівниками різних професій - ВВП І ЗАГАЛЬНИЙ РІВЕНЬ ЦІН
індексів. Принципова модель цінового індексу: Існує безліч цінових індексів, найбільш загальним з них є дефлятор - ВІДСТЕЖЕННЯ NASDAQ-КОМПОЗИТ
індексу. Він надзвичайно волатильним і схильний до захоплюючих дух підйомів і спустошливим розпродажів за зниженими цінами, навіть коли Індекси Доу і S & P залишаються - Дефлятор ВНП та індекс цін
індекси цін для обчислення реального ВНП. Відношення між номінальним і реальним ВНП - показник, званий дефлятором ВНП: Номінальний ВНП Дефлятор ВНП=- Реальний ВНП 2. Показники функціонування національної економіки 305 Дефлятор ВНП вимірює інтенсивність інфляції або зворотного процесу - дефляції. Якщо величина індексу цін більше 1, то сталося дефлювання - Вимірювання інфляції
індексів цін. Відомі індекс зростання цін Ласпейраса (це індекс споживчих цін), індекс зростання цін Пааше (індекс цін виробників), індекс зростання цін Фішера (див. докладніше гол. 12, п. 2). Якщо індекс споживчих цін враховує тільки вартість споживчого кошика, то в цілому по економіці судити про динаміку цін правильніше по дефлятора ВНП, бо він охоплює всі види товарів - - Вимірювання інфляції
індексів цін. Відомі індекс зростання цін Ласпейраса (це індекс споживчих цін), індекс зростання цін Пааше (індекс цін виробників), індекс зростання цін Фішера (див. докладніше гол. 12, п. 2). Якщо індекс споживчих цін враховує тільки вартість споживчого кошика, то в цілому по економіці судити про динаміку цін правильніше по дефлятора ВНП, бо він охоплює всі види товарів - - ЗАСТОСУВАННЯ ф'ючерси на S & P 500 Як індикатор стійкого підйому
цінами, у той час, як Доу продовжує зростати, це вірна ознака того, що підйом Доу - 2. Вимірювання і показники інфляції
індекси цін, у тому числі індекси цін в споживчому секторі - Терміни і поняття
цін Індекси Ласпейреса, Пааше і Фішера Повзуча інфляція Галопуюча інфляція Гіперінфляція «Імпортується» інфляція Інфляційні очікування Дефляційна - Коли економісти вивчають зміни обмінних курсів, вони ис- товують індекси, які усереднюють численні
індекси, які усереднюють численні обмінні курси. Подоб-але тому як індекс споживчих цін перетворює вартості безлічі това-рів до єдиного показника рівня цін, так і індекс обмінного курсу наводить численні обмінні курси до єдиного показника міжнародної стоїмо-сті валюти. Тому, коли економісти говорять про підвищення або зниження курей-са долара, вони нерідко - 32. НАЦІОНАЛЬНИЙ ДОХІД. ІНДЕКСИ ЦІН. Наявний особистий ДОХІД
індексу споживчих цін (ІСЦ). Реальний наявний дохід - це кількість товарів і послуг, яку можна купити на наявний дохід протягом певного періоду, тобто це наявний дохід з поправкою на ІСЦ. ІСЦ розраховується відповідно до Основних положень про порядок спостереження за споживчими цінами і тарифами на товари та платні послуги, надані населенню, і - Індекси Ласпейреса, Пааше і Фішера
індексувати) зростання цін, то це не складе особливих труднощів. Ціни базового року можна прийняти за 100%, а ціни наступних років перерахувати по відношенню до цього року. Так, якщо середня ціна бензину в звітному 1998 р. становило 1100 руб. за тонну, а в базовому 1997 1000 руб. за тонну, то індекс цін на бензин склав: (1100:1000). 100==110%. Таким чином, середня ціна в звітному році по - Питання для самоперевірки
індекс споживчих цін за цей же період склав 16%. Як змінилися реальні доходи населення? 6. Чим характеризується бідність в Росії і які її масштаби? 7. Що таке індексація доходів і яка її соціальна