11.2.2.1. МОДЕЛЬ БЕРТРАН
дуополіст Бертрана в усьому подібні дуополіст Курно, відмінно лише їх поведінку.
Дуополіст Бертрана виходять із припущення про незалежність цін, установлюваних один одним, від їх власних цінових рішень. Інакше кажучи, не випуск суперника, а призначена ним ціна є для дуополіст параметром, константою. Для того щоб краще зрозуміти відмінність моделі Бертрана від моделі Курно, представимо її також в термінах ізопрофіт і кривих реагування.
У зв'язку із зміною керованої змінної {з випуску на ціну) і ізопрофіти, і криві реагування будуються в двомірному просторі цін, а не випусків.
Змінюється і їх економічний сенс. Ізопрофіти і криві реагування дуополістів Бертрана представлені на рис. 11.6. Тут ізопрофіта, або крива рівного прибутку, дуополіст 1 - це безліч точок у просторі цін (P1, P2), відповідних комбінаціям цін P1 і P2, які забезпечували б дуополіст одну і ту ж суму прибутку. Відповідно ізопрофіта дуополіст 2 - це безліч точок в тому ж просторі цін, відповідних комбінаціям (співвідношенням) цін З1 і P2, що забезпечує одну і ту ж прибуток дуополіст 2. Сімейства таких кривих рівної прибутку, або ізопрофіт дуополістів 1 (? 11,? 21,? 31,? 41) і 2 (? 12,? 22,? 32,? 42), представлені на рис. 11.6. Ізопрофіти дуополіст 1 випуклі до осі його ціни (P1), а дуополіст 2 до осі його ціни (P2).
Така конфігурація ізопрофіт означає, що дуополіст 1 повинен буде знизити ціну до певного рівня, наприклад з P'1 до P'' 1, щоб зберегти свій прибуток незмінною (залишитися на ізопрофіте? 21) у разі зниження дуополіст 2 своєї ціни з P'2 до P'' 2.
Однак, якщо і після цього дуополіст 2 продовжить знижувати свою ціну, дуополіст 1 не зможе зберегти свій прибуток незмінною. Очевидно, що при скільки-небудь більш низькою, ніж P'' 2, ціною дуополіст 2 дуополіст 1 повинен буде перейти на більш низьку, ніж? 21, ізопрофіту, а це означає, що величина його прибутку зменшиться. Чим ближче до осі ціни лежить ізопрофіта відповідного дуополіст, тим нижчий рівень рівної прибутку вона відображає.
Таким чином, при будь-якій зміні ціни дуополіст 2 існує єдина ціна дуополіст 1, максимизирующая його прибуток. Ця прібилемаксімізірующая ціна визначається найнижчою точкою найбільш високо лежить ізопрофіти дуополіст 1.
Такі точки (e1 - q4 на рис. 11.6, а) у міру переходу до більш високих ізопрофітам зміщуються вправо. Це означає, що, збільшуючи свій прибуток, дуополіст 1 робить це за рахунок залучення покупців дуополіст 2, що підвищує свою ціну, навіть якщо при цьому дуополіст 1 теж збільшує ціну. Поєднавши найбільш низько лежать точки всіх послідовно розташованих ізопрофіт, ми отримаємо криву реагування дуополіст 1 на зміни цін дуополіст 2 - R1 (P2) на рис. 11.6, а. Абсциси точок цієї кривої являють собою прібилемаксімізірующіе ціни дуополіст 1 при заданих ординатами цих точок цінах дуополіст 2. Відповідно лінія R2 (P1) на рис-11.6, б представляє криву реагування дуополіст 2 на безлічі його ізопрофіт (? 12,? 22,? 32,? 42). Тепер, знаючи криві реагування дуополістів Бертрана, ми можемо визначити рівновагу Бертрана як інший (порівняно з рівновагою Курно) окремий випадок рівноваги Неша, коли стратегія кожного підприємства полягає не у виборі ним свого обсягу випуску, як у випадку рівноваги Курно, а у виборі їм рівня ціни, за якою він має намір реалізувати свій випуск.
Рівновага Бертрана - Неша представлено точкою В - N на рис. 11.7. Зверніть увагу на те, що обидві криві реагування Бертрана на відміну від кривих реагування Курно (рис. 11.3) висхідні. Це означає, що ціни дуополістів Бертрана мають виражену тенденцію до зближення на противагу випускам дуополістів Курно.
Рівновага Бертрана досягається, якщо припущення дуополістів про ціновій поведінці один одного збуваються. Якщо дуополіст 1 вважає, що його суперник встановить ціну P12 (рис. 11.7), він з метою максимізації прибутку вибере, згідно своєї кривої реагування, ціну P11. Але в такому випадку дуополіст 2 може насправді встановити на свою продукцію ціну P22, виходячи зі своєї кривої реагування. Якщо припустити (як ми це робили при розгляді рівноваги Курно), що крива реагування дуополіст 1 крутіше, ніж відповідна крива дуополіст 2, то тоді цей ітеративний процес призведе дуополістів до рівноваги Бертрана - Неша (тобто в точку В - N на рис . 11.7), де їх криві реагування перетнуться. Маршрут їх конвергенції в точку В-N виявиться подібний маршрутом конвергенції випусків дуополістів Курно, показаному стрілками на рис. 11.4. Оскільки продукція обох дуополістів однорідна, кожен з них вважатиме за краще в стані рівноваги один і той же рівень її ціни. В іншому випадку дуополіст, який призначив більш низьку ціну, захопить весь ринок. Тому рівновага Бертрана-Неша характеризується єдиною ціною, що належить в двомірному просторі цін променю, що виходить з початку координат під кутом 45 градусів. Крім того, в стані рівноваги Бертрана-Неша рівноважна ціна виявиться рівної граничним витратам кожного з дуополістів. В іншому випадку дуополіст, керуючись кожен прагненням оволодіти всім ринком, будуть знижувати свої ціни, а це їх прагнення може бути паралізовано, лише коли вони зрівняють свої ціни не тільки між собою, але і з граничними витратами. Природно, що в цьому випадку загальна галузева прибуток виявиться нульовий.
Таким чином, незважаючи на виняткову нечисленність продавців (в дуополии їх лише двоє), модель Бертрана пророкує, по суті справи, абсолютно конкурентну рівновагу галузі, яка має будову дуополии. [10] Нехай, як і в моделі Курно (11.6), ринковий попит представлений лінійною функцією Р=а - bQ, де Q=q1 + q2. Тоді зворотна функція попиту буде:
Q=q1 + q2=(a / b) v (1 / b) P (11.53)
Якщо при даній ціні дуополіст 1, P1> МС, дуополіст 2 встановлює ціну З2> МС, залишковий попит дуополіст 1 залежатиме від співвідношення цін P1 і P2. А саме при P1> P2, q1=0 всі покупці, залучені більш низькою ціною, перейдуть до дуополіст 2. Навпаки, при P1
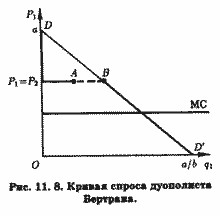
На рис. 11.8 функція попиту дуополіст 1 відображена має розрив (АВ) кривої попиту DP2ABD '.
При P1=P2 ринок буде поділено порівну (сегмент P2А належатиме дуополіст 1, а сегмент АВ дуополіст 2). Нарешті, якщо дуополіст 1 відповість на P2 зниженням своєї ціни нижче цього рівня, він захопить весь ринок (сегмент BD '). З рис. 11.8 також видно, що кожне з підприємств-дуополістів може залишатися рентабельним, потроху знижуючи ціну з метою збільшення своєї частки ринкового попиту до тих пір, поки не буде досягнуто рівність:
P1=P2=MC, (11.54)
яке і характеризує стан рівноваги Бертрана-Неша.
Таким чином, на відміну від моделі Курно, що пророкує досягнення зовсім конкурентного результату лише в міру збільшення числа олигополистов, а саме коли п / (п + 1) наближається до одиниці, модель Бертрана передрікає абсолютно конкурентний результат відразу ж при переході від монополії одного продавця до дуополии. Причина цього кардинального відмінності висновків у тому, що кожен дуополіст Курно стикається з низхідній залишкової кривої попиту, тоді як дуополіст Бертрана - з кривою попиту цілком еластичною за ціною суперника, так що зниження ціни виявляється прибутковим, поки вона залишається вище граничних витрат. У табл. 11.2 наведені рівноважні випуски і ціни, що передбачаються моделями Курно і Бертрана, а також моделями монополії і досконалої конкуренції.
Таблиця 11.2 Рівноважні обсяги випуску і ціни в моделях Курно і Бертрана за досконалої конкуренції і монополії
| Модель | Ціна | Випуск галузі |
| Монополії Курно (n=2) Курно (n / (n + 1) ? 1) Бертрана (n=2) Зробленої конкуренції |
(a + c) / 2 a / 3 + 2c / 3 ? c c c |
(a - c) / 2b 4/3 (a - c) / 2b ? (A - c) / b (a - c) / b (a - c) / b |
Після вивчення моделей Курно і Бертрана, що пророчать при п=2 істотно різні результати, у вас виникне природне запитання, чия модель "краще", "правильніше", словом, яку з них слід використовувати при аналізі олігополії. Перш ніж спробувати відповісти на нього, подумаємо ось над чим. Мало того, що дуополіст Курно і Бертрана "наївні" і не здатні коригувати свою поведінку під впливом досвіду або, як часто говорять, не здатні до "навченню справою" (англ, learning by duing), вони наділені ще одним, зручним для побудови моделі , але дуже нереалістичним, властивістю - їх виробничі потужності буквально "безрозмірні" і здатні стискатися і розширюватися, як гумові. Адже дуополіст можуть, не несучи ніяких додаткових витрат, вільно варіювати обсяг свого випуску від нуля до величини, рівної всьому ринкового попиту. При цьому їх граничні і середні витрати залишаються незмінними, яка-небудь економічність або неекономічність від масштабу відсутня. Ввести в модель Бертрана обмеження потужності запропонував Ф. Еджуорт.
Інформація, релевантна " 11.2.2.1. МОДЕЛЬ Бертран "
- 11.2.2. ЦІНОВА ОЛІГОПОЛІЯ
Традиційно економісти беруть не ціну, а кількість (величину випуску) як керованої (або стратегічної) змінної підприємства. Дійсно, при досконалої конкуренції, коли підприємства є ценополучателем, величина випуску, як ми бачимо, є єдина змінна, керована самим підприємством. Навпаки, за недосконалої конкуренції підприємство, як ми пам'ятаємо, може - 11.2.2.3. КІЛЬКІСНА АБО ЦІНОВА ОЛІГОПОЛІЯ?
Інтуїтивно можна припустити, що модель цінової конкуренції більш реалістично представляє поведінка олігополіс-тов, ніж модель кількісної олігополії. Причиною тому може бути велика легкість маніпулювання цінами, ніж обсягами випуску. Для того щоб варіювати обсяги випуску, можуть знадобитися і додаткові інвестиції у виробничі потужності, і час. Варіювати цінами - Терміни і поняття
Конкуренція Ефективність конкурентних ринків «Життєвий цикл» Види конкуренції: видова, функціональна, межфирменная, внутрішньогалузева, міжгалузева, сумлінна, недобросовісна, досконала, недосконала Види конкурентних структур: досконала конкуренція, монополії, монопсонії, олігополії, дуополии, монополістична конкуренція Методи і засоби конкурентної боротьби - 11.2.2.2. МОДЕЛЬ Еджуорта
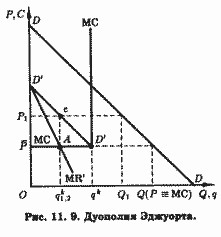
Погодившись з критикою моделі Курно Бертраном, Ф. Еджуорт запропонував модель цінової дуополии з обмеженням на величину виробничої потужності дуополіс-тов. [11] На рис. 11.9 це обмеження представлено абсциссой вертикально висхідного сегмента кривої МС (витрати на виробництво додаткової - понад обмеженого масштабу потужності - одиниці продукції нескінченно великі) qk. Як видно з рис. - Запитання для самоперевірки
1. Що таке конкуренція і монополія? Які їх переваги і недоліки? 2. Охарактеризуйте взаємозв'язок конкуренції і монополії. 3. Які види конкурентних структур ви знаєте? Які критерії можна запропонувати для оцінки різних структур ринку? 4. Що з переліченого нижче є ознакою тільки абсолютно! конкуренції: а) фірма не має ринкову владу, б) фірма - Запитання для самоперевірки
1. Що таке конкуренція і монополія? Які їх переваги і недоліки? 2. Охарактеризуйте взаємозв'язок конкуренції і монополії. 3. Які види конкурентних структур ви знаєте? Які критерії можна запропонувати для оцінки різних структур ринку? 4. Що з переліченого нижче є ознакою тільки абсолютно! конкуренції: а) фірма не має ринкову владу, б) фірма - Моделі фондової біржі та позабіржового ринку
У чому ще відмінності англо-американської моделі фондового ринку від західноєвропейської? Схематично їх суть можна зобразити таким чином: в одній моделі контрольні пакети акцій зазвичай невеликі і тому основна їх маса вільно обертається на ринку; в іншій моделі переважна частка акцій - в контрольних пакетах і, отже, на ринку обертається відносно небагато акцій. Першу модель - 3. Стандартна модель міжнародної торгівлі
Використовувана в даний час стандартна модель міжнародної торгівлі об'єднує різні теорії, розвиваючі фундаментальні положення класичних теорій на основі використання концепцій граничних величин і загальної рівноваги економічної системи. Базові поняття стандартної моделі були розроблені англійськими економістами Френсісом Еджуорта і Альфредом Маршаллом і американським - Спроба структурного підходу
Обмеженість моделі номінального доходу, на думку пеко торих монетаристів, пов'язана насамперед з тим, що ця модель ш враховує структурні зрушення на ринку позичкового капіталу, які неминучі при проведенні кредитно-грошових заходів. Peiu. йде насамперед про вплив цих заходів на структуру процен i них ставок, а через них - на сукупні витрати та їх структуру. Особливу увагу - ЛЮДИ, ПРАВА І СВОБОДИ
У прочитаної Вами книзі викладені ази економіки. Як і прийнято звичайно в економічній науці ці ази викладаються й обгрунтовуються, виходячи з принципів максимізації виробництва суспільних благ, найбільш раціонального та ефективного використання ресурсів та ін Але крім такого - економічного - підходу до організації суспільного життя і взаємодій суспільства і держави, - 1.1. Модель кругообігу реальних і грошових потоків
У моделі кругообігу виділяються два сектори: реальний сектор (потік ресурси-продукція) і грошовий сектор (потік доходи-витрати). Проста модель кругообігу в закритій економіці без держави показана на рис. 1.1. Рис. 1.1. Проста модель кругообігу в закритій економіці без держави: --- реальні потоки; --- грошові потоки З введенням держави в модель кругообігу - 22.3. Модель господарського механізму Японії
На високі темпи зростання японської економіки був націлений її господарський механізм, що склався в другій половині XX в., Своєрідність рис якого дозволяє говорити про особливу - Хто мій клієнт?
Кожен бізнес має центральну демографічну модель. Тут мається на увазі найбільш ймовірний клієнт. Цей клієнт має набір характеристик - вік, стать, дохід, сімейний стан, освіту і т.д. Ваш клієнт звертається до вас за дуже специфічним причин, жодна з яких не є раціональною або навіть зрозумілої! Він або купує, або нет.Мотівація клієнта становить ядро - Практичні завдання
1. Зобразіть модель кругових потоків за участю держави для відкритої економіки. 2. Продумайте і позначте на графіку, які частини моделі кругових потоків пов'язані з потоками продуктів і грошових коштів при економі-чеських процесах і видах діяльності, які ви здійснювали протягом останніх - Глава 7. Революція готової моделі
Теорія систем розглядає всі явища в світі з точки зору їх взаємозв'язку; таким чином, системою називається інтегроване ціле, яке є чимось більшим, ніж проста сума його частин. Фрітьоф Капра "Поворотний момент" Ми всі знайомі з такими сучасними явищами, як індустріальна революція, технічна революція та інформаційний вибух. Ніхто не стане сперечатися, що вони - Терміни і поняття
Сукупний попит Сукупна пропозиція Макроекономічна рівновага Рівновага на товарному і грошовому ринках «Пастка ліквідності» Модель AD-AS Модель IS-LM Макроекономічна неравновесность Умови загальної рівноваги Закон Вальраса Теорія макроекономічної рівноваги - Контрольні питання
1. Які основні методи застосовуються в макроекономіці і в чому сутність кожного з них? 2. Що є предметом, а що об'єктами макроекономіки? 3. Які основні цілі макроекономічної політики? 4. Що таке національна економіка і які її основні цілі? 5. Що таке світове господарство? 6. Які основні напрямки теоретичної думки в економічній науці та їх характерні