11.2.1.1.1. ЧИСЛОВА ВЕРСІЯ
Курно припустив, що існують дві фірми, кожна з них володіє джерелом мінеральної води, який вона може експлуатувати з нульовими операційними витратами. Свій випуск (мінеральну воду) вони продають потім на ринку, попит на якому заданий лінійною функцією. Кожен дуополіст виходить з припущення, що його суперник не змінить свого випуску у відповідь на його власне рішення. Це означає, що, приймаючи його, дуополіст керується прагненням до максимізації свого прибутку, вважаючи випуск іншого дуополіст заданим (dq2/dq1=0, dq1/dq2=0,).

Припустимо, що першим починає видобуток води дуополіст 1, так що на першому кроці він виявляється монополістом. Очевидно (рис. 11.1), що його випуск складе тоді q1, що при ціні Р забезпечує йому максимальний прибуток, оскільки в цьому випадку MR=МС=0 - Еластичність ринкового попиту при такому випуску дорівнює одиниці, а загальна виручка досягає максимуму, що при нульових витратах тотожне максимуму прибутку.
Потім видобуток мінеральної води починає дуополіст 2. В його уяві ордината графіка на рис. 11.1 зрушена вправо на величину Oq1 і, таким чином, поєднана з лінією Aq1. Сегмент AD 'кривої ринкового попиту DD' він сприймає як криву залишкового попиту (англ, residual demand curve), якій відповідає крива його граничної виручки, MR2. Очевидно, що прібилемаксімізірующій випуск дуополіст 2 складе половину незадоволеного дуополіст 1 попиту, тобто сегмента q1D '.
Значить, величина його випуску складе q1q2, що забезпечить йому (але тим же, що і дуополіст 1, причин) максимум виручки і, отже, прибутку. Зауважимо, що цей випуск складе чверть всього ринкового обсягу попиту при нульовій ціні, OD '(1/2 - 1/2=1/4). На другому кроці дуополіст 1, вважаючи, що випуск дуополіст 2 залишиться незмінним, вирішить покрити половину залишився все ще незадоволеним попиту. Оскільки дуополіст 2 покриває чверть ринкового попиту, випуск дуополіст 1 на другому кроці складе 1/2 (1 - 1/4), тобто 3/8 всього ринкового попиту, і т. д. Легко переконатися в тому, що з кожним наступним кроком випуск дуополіст 1, який першим розпочав експлуатацію свого джерела і тому одразу ж опинився в положенні монополіста, буде скорочуватися, тоді як випуск дуополіст 2 , "проспав" перший крок, буде зростати. Цей процес завершиться уравниванием їх випусків, і тоді дуополія досягне стану рівноваги Курно.
Дійсно, при кожному послідовному кроці q1 складе (в частках загального ринкового попиту):
1) 1/2,
2) 1/2 (1 v 1/4)=3/8=1/2 v 1/8, (11.5)
3) 1/2 (1 v 5/16)=11 / 32=1/2 v 1/8 v 1/32,
4) 1/2 (1 v 42/128)=43/128=1/2 v 1/8 v 1 / 32 v 1/128,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Систему (11.5) можна узагальнити, представивши випуск дуополіст 1 в стані рівноваги, q * 1, як:
q * 1=1/2 v 1/8 v 1/32 v 1/128 -
або:
q * 1=1/2 v [1/8 + (1/8) (1 / 4) + (1/8) (1/4) 2 + (1/8) (1/4) 3 + -].
Тут вираз у квадратних дужках є не що інше, як нескінченно спадна геометрична прогресія з першим членом q1 і знаменником 1/4. Тоді рівноважний випуск дуополіст 1 можна визначити як різницю між 1/2 і сумою членів цієї нескінченно спадної прогресії:
q * 1=1/2 v (1: 8) / (1 v 1: 4)=1/2 v (1: 8) / (3: 8)=1/3.
Таким чином, рівноважний випуск дуополіст 1 складе одну третину ринкового обсягу попиту.
Аналогічно можна підрахувати і рівноважний випуск дуополіст 2. При кожному послідовному кроці його випуск, q2, складе:
1) 0,
2) (1/2) (1/2)=?
3) (1/2) (1 v 3/8)=5/16 1/4 + 1/16,
4) (1/2) (1 - 11/32)=21/64=1/4 + 1/16 + 1/64,
5) (1/2) (1 v 43/128)=85 / 256=1/4 + 1/16 + 1/64 1/256,
. . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Випуск дуополіст 2 зростає, хоча і в снижающемся темпі. Тепер ми можемо уявити рівноважний випуск другого дуополіст, q * 2, як суму:
q * 21/4 + (1/4) (1/4) + (1/4) (1 / 4) 2 + (1/4) (1/4) 3
Використовуючи знову формулу суми членів нескінченно спадної геометричної прогресії, одержимо:
q * 2 (1 : 4) (1 1: 4)=(1: 4) (3: 4)=1/3.
Таким чином, в стані рівноваги кожен з дуополістів Курно покриває своєю продукцією третину ринкового попиту при єдиній ціні. Покриваючи спільно дві третини ринкового попиту, кожен дуополіст забезпечує максимум своєї, але не галузевий прибутку. Вони могли б, мабуть, збільшити свою загальну прибуток, якби, зрозумівши помилковість своїх припущень щодо заданості обсягів випуску один одного, вступили б у явний або таємна змова і діяли як єдина монополія (легально чи нелегально). У цьому випадку ринок виявився б поділеним навпіл, так що кожен з них покривав би по чверті (замість третини) ринкового попиту по прібилемаксімізірующей ціною.
Курно неодноразово дорікали за наївність його моделі дуополії. Насамперед дуополіст не роблять ніяких висновків з помилковості своїх припущень щодо реакції суперників. Крім того, модель Курно закрита, кількість підприємств з самого початку обмежена і не змінюється в ході руху до рівноваги.
Модель нічого не говорить про можливу тривалість цього руху.
Нереалістичним представляється і допущення про нульові операційних витратах.
Деякі з цих "вроджених" недоліків (по суті - спрощень) можуть бути елімінувати при включенні в модель Курно так званих кривих реагування.
Однак, перш ніж включити їх в модель Курно, доцільно зупинитися на важливою проміжною характеристиці - ізопрофітах, або кривих рівної прибутку.
У широкому сенсі ізопрофітамі називають безліч комбінацій двох або більше незалежних змінних функції прибутку, що забезпечують одну і ту ж суму прибутку. У моделі дуополії Курно іеопрофіта, або крива рівного прибутку дуополіст 1, - це безліч точок у просторі випусків (q1, q2), відповідних комбінаціям (наборам) випусків обох дуополіетов, що забезпечують дуополіст 1 один і той же рівень прибутку.
Перерахуємо коротко основні характеристики та властивості ізопрофіт.
1. Уздовж ізопрофіти величина прибутку дуополіст незмінна. Так, наприклад, уздовж ізопрофіти? 21 (рис. 11.2, о)? 1=? 1 (q1, q2)=const, а вздовж іеопрофіти? 12 (рис. 11.2,6)? 2=? 2 (q1, q2)=const.
2. Ізопрофіти увігнуті до осей, на яких відображається випуск того дуополіст, чия ізопрофіта представлена на малюнку. Так, ізопрофіти дуополіст 1 увігнуті щодо осі його випуску. Така форма ізопрофіти показує, як дуополіст 1 може реагувати на ухвалене дуополіст 2 рішення про величину випуску з тим, щоб його рівень прибутку не змінився.
3. Чим далі відстоїть ізопрофіта від осі випуску даного олигополиста, тим менший рівень прибутку вона відображає. І навпаки, чим ближче лежить ізопрофіта до осі випуску даного дуополіст, тим більшого рівня прибутку вона відповідає.
4. Для будь-якого заданого випуску олигополиста 2 існує єдиний рівень випуску олигополиста 1, максимізує прибуток останнього. Для дуополіст 1 такий випуск визначається (при даному випуску дуополіст 2) найвищою точкою на нижчої з доступних йому ізопрофіт.
5. Вищі точки ізопрофіт дуополіст 1 зміщені вліво, так що, з'єднавши їх однією лінією, ми одержимо криву реагування (англ, reaction curve).
На рис. 11.2, a R1 (q2) - крива реагування дуополіст 1 на величину випуску, запропонованого дуополіст 2, a К2 (q1) на рис. 11.2, б - крива реагування дуополіст 2 на величину випуску, запропонованого дуополіст 1.
Криві реагування - це множини точок найвищої прибутку, яку може отримати один з дуополіетов при даній величині випуску іншого.
Множини цих точок називають кривими реагування, оскільки вони вказують на те, як один з дуополіетов, вибираючи величину свого випуску, qi, реагуватиме на рішення іншого дуополіст щодо величини свого випуску, qj (i? J).
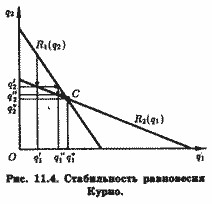
Нерідко, особливо в теоретика-ігрових моделях олігополії, криві реагування називають кривими найкращого відповіді (англ, best response). Точка перетину кривих реагування обох дуополіетов, суміщених в одному двомірному просторі випусків, визначає рівновагу Курно.
Інформація, релевантна " 11.2.1.1.1. ЧИСЛОВА ВЕРСІЯ "
- ОСНОВНІ ПОНЯТТЯ
СТАТИСТИКА - 1. Сфера прфессионально діяльності, що охоплює збір, подання, аналіз та інтерпретацію числових даних. 2. Інформація, дані, необхідні для прийняття рішень, офіційно опубліковані показники, що характеризують окремі галузі діяльності, в тому числі господарської. УНІФІКАЦІЯ СТАТИСТИЧНИХ ДАНИХ - приведення до єдиного вигляду і методам розрахунків, які використовуються різними - Тести
1. Загальна економічна рівновага - це: а) оптимальна збалансованість економічної системи; б) рівновага, стале в окремих галузях і сферах економіки; в) рівновага економічної системи в цілому. 2. На якій конфігурації кривої сукупної пропозиції наполягають кейнсіанці: а) лінія, паралельна осі ОХ; б) лінія, паралельна осі OY; в) лінія з негативним - Як перевірити знання на практиці?
Після того як ви прочитали книгу, чи виникло у вас бажання про-вірити ваші знання на практиці? Якщо так, тоді мої зусилля були не марними і повірте, прекрасний світ трейдингу зачарує вас ще більше після того, як ви випробуєте першу перемогу над ринком, над самим собою і пройдете через першої поразки. Перш ніж приступити до торгівлі з реальними грошима спробуйте свої сили на - Паперові тестові картки
малопродуктивних прості переліки слів з повчанням студентам по їх засвоєнню. Існують інші можливості засвоєння категоріального апарату економічних наук? тести. Розроблена тестология дозволяє відібрати найбільш плідний тип тестів? категоріальні тести відповідності. Підготовлений словник перетворюється на систему паперових тестових завдань. На кожному аркуші дають 20 визначень і 25 - 5.6. Використання коефіцієнтів Фібоначчі в Хвильовий Теорії Елліотта
Числа Фібоначчі є однією з двох складових у професійній методології Хвильовий Теорії Елліотта. Саме Елліотт зробив послідовність Фібоначчі однією з основ теорії технічного аналізу. І саме в Хвильовий Теорії числах Фібоначчі відводиться таке почесне місце. Вони роблять можливим визначення довжини розвитку кожної з хвиль як за ціною, так і за часом. Корисність - 4.4. Повертаємося до розвитку форм і методів робіт з якості
Після розгляду схем механізму управління якістю, складу та змісту спеціальних функцій управління якістю, форм відображення систем якості в їх моделях повернемося до питань послідовної еволюції підходів до управління якістю. Тепер можна на більшій фактичному матеріалі простежити цей процес. Вельми вдало в графічній формі цей процес відображений у статті професора К. - 2. Вимірювання економіческіхпеременних
У більшості своїй економічні переменниепредставлени швидше кількістю тракторів ілікурсамі акцій, ніж споживчими установкамі.Оні легко і вичерпним чином можуть битьохарактерізовани за допомогою чисел. Государствен-ні агентства збирають і публікують щорічно го-ри числової інформації, так само як і приватні дже-рел, наприклад American Newspaper PublishersAssociation і American - 1.2.4 СУКУПНИЙ ПОПИТ І ПРОПОЗИЦІЯ
Попит та пропозиція вивчають на різних рівнях: індивідуальний? ринковий? сукупний. Індивідуальний і ринковий попит розглянуто при аналізі законів вільного ринку. Сукупний попит і пропозиція показують в цілому ці аспекти ринку країни. Головна мета їх аналізу? з'ясувати фактори попиту та пропозиції, функціональні зв'язки між основними їх чинниками, умови рівноваги, як і причини - , а також значення чотирьох його складаючи-чих.
, А також значення чотирьох його складаючи-чих. ВСЬОГО, S МЛРД НА ДУШУ НАСЕЛЕННЯ, S До ПІДСУМОК /, У% ВВП 7576 Споживання 5152 Інвестиції 1116 Державні закупівлі 1407 Чистий експорт -99 28 589 1944 1 4211 5309 -373 100 68 15 19 -1 Джерело: US Department - Проблема вибору між інфляцією та безробіттям за останні 40 років породила чимало сум'яття
Проблема вибору між інфляцією та безробіттям за останні 40 років породила чимало сум'яття в умах, проте сьогодні бал править згоду в думках. От як ви-позначався в 1968 р. про зв'язок між інфляцією та безробіттям Мілтон Фрідмен: Існує тільки тимчасова зворотна залежність між інфляцією і безробіттям, грунтується не на інфляції per se (самої по собі, (лат.) - Прим. Перекл.), а - : від кривої Філліпса, розробленої і дослідженою А.
: від кривої Філліпса, розробленої і дослідженою А. Філліпсом, П.Самуельсоном і P. Солоу, через гіпотезу природного рівня M. Фрідмена і Е. Фелпса, до теорії раціональних очікувань P. Лукаса, T. Сарджента і P. Барро. Четверо з названих вище вже удостоїлися Нобелівської премії за внесок в економічну науку, решті, впол-ні ймовірно, ще доведеться брати участь у церемонії - 11.2.1.1.2. АНАЛІТИЧНА ВЕРСІЯ
Проведемо тепер більш строгий аналітичний висновок рівноваги Курно, відмовившись від ряду зроблених раніше "наївних" припущень: квазідінаміческого характеру наближення до рівноваги шляхом серії послідовних кроків і нульових операційних витрат. Покладемо, що кожен дуополіст (у всіх відношеннях ідентичний супернику) прагне до максимізації свого прибутку, виходячи з припущення, що другий