Додаток 2А. Ціна як статистична характеристика ринку
У моделях ринкової рівноваги, у тому числі і у використовуваних в главі 2, попит і пропозиція зазвичай представлені безперервними функціями. Передбачається, що всякому малому зміни ціни відповідає певна зміна обсягів попиту та пропозиції. Таке припущення, як ми вже бачили (рис. 2.13), не завжди реалістично. Безперервна зміна ціни не обов'язково супроводжується безперервним ж зміною обсягів попиту та пропозиції, які можуть змінюватися стрибкоподібно, залишаючись нечутливими до малих змін ціни. У цьому випадку функції попиту та пропозиції мають ступінчастий характер.
Використовуючи деякі елементи теорії множин, можна запропонувати досить загальну модель рівноважної ціни, справедливу як для безперервних, так і для дискретних функцій попиту та пропозиції.
При цьому виявляється, що рівноважна ціна може бути представлена як медіана впорядкованої множини цін попиту та пропозиції. [13]
Нехай максимально можливий обсяг пропозиції деякого товару становить QSK (рис. 2.8, QK) - Нехай, далі, всі можливі ціни пропозиції цього товару представлені безліччю:
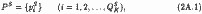
а всі можливі ціни попиту - безліччю:
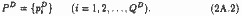
Очевидно, що ці безлічі можуть виявитися кількісно еквівалентними або рівнопотужними (QSK=QD) лише випадково. Швидше за все, потужність множини PD буде більше потужності множини PS (QD> QSK)> хоча можливо і зворотне (QD
Тут нескінченно високі ціни пропозиції означають неможливість збільшити обсяг пропозиції ні при якому розумному рівні витрат.
Нульові ціни попиту свідчать про обмежену в силу якихось причин ємності ринку.
Тепер ми маємо два кількісно еквівалентних безлічі:
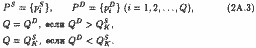
Очевидно, що при будь-якому рівні ринкової ціни (р) алгебраїчна сума відхилень від неї всіх цін попиту та пропозиції дорівнюватиме сумарним надлишку покупців і продавців:
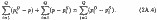
При цьому взаємовигідним обмін буде лише для тих покупців і продавців, у яких величина надлишку буде неотрицательной, а невзаімовигодним для тих, у кого вона виявиться непозитивно [14] (рис. 2.24).
Отже, рівноважна ринкова ціна (р *) повинна на відміну від будь-якої іншої забезпечувати рівність суми модулів відхилень від неї цін попиту та пропозиції різниці Q * невід'ємних і (Q - Q *) непозитивним сум суспільної вигоди по всіх Q одиницям товару (Q * - рівноважний обсяг ринку при ціні p *: [15]
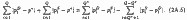
А оскільки сума абсолютних значень двох величин не може бути менше їх алгебраїчної суми, то:
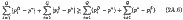
і, отже:
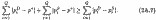
З урахуванням (2А.7) вимога (2А.5) може бути переписано так:
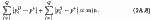
Останнє означає, що сума модулів відхилень всіх цін попиту та пропозиції від рівноважної ціни р * менше, ніж від будь-якої іншої величини. Але такою властивістю володіє лише медіана (Me) всієї сукупності цін попиту та пропозиції. У цьому легко переконатися. Об'єднаємо безлічі PD і PS в єдине упорядкований безліч :
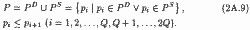
Тоді (2А.9) можна переписати так:
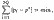
або, приймаючи, що:
pk? p * & le pk +1, k=i? (1, 2, ... Q -1)
розгорнуто:
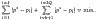
Диференціюючи і прирівнюючи нулю, знайдемо:
-k + (2Q - k)=0,
звідки k=Q.
Отже:
pQ? p *? pQ +1
Останнє означає, що рівноважна ціна р * ділить упорядкований безліч цін попиту та пропозиції (2А.9) на два кількісно еквівалентних підмножини:
P '={pi | pi? PD V pi? PS}, (2A.10)
pi? pi +1 (i=1, 2, ..., Q)
і:
P '={pi | pi? PD V pi? PS}, (2A.11)
pi? pi +1 (i=Q + 1, Q + 2, ..., 2Q)
причому:
PQ? P *? PQ +1 (2A.12)
тобто є центральною величиною, або медіаною (2А.9):
Р *=Me (Pi). (2A.13)
З (2А.10) і (2А.11) видно, що, розділяючи безліч (2А.9) на підмножини Р 'і Р ", медіана тим самим поділяє і вихідні безлічі РD і РS на підмножини:
,
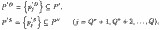
і доповнення до них:
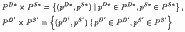
такі, що для координат їх декартових творів:
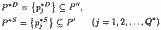
виконуються відносини:
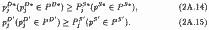
Таким чином, рівна медіані рівноважна ціна (р *=Me (рi)) відокремлює одиниці товару з неотрицательной різницею між ціною попиту та ціною пропозиції (2А.
Якщо (2А.14) виконується як суворе рівність і, отже, перетин множин Р 'і Р "непорожньо, то медіана суть це перетин :
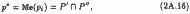
або:
pQ=Me (pi)=pQ +1
(рис. 2.13, б)
Якщо ж (2А.14) виконується як нерівність, рівноважна ціна може приймати будь-яке значення в межах медіанного інтервалу:

або:
pQ? p *? pQ +1
(рис. 2.13, а).
Проілюструємо визначення рівноважної ціни як медіани впорядкованої множини цін попиту та пропозиції аналізом відомого прикладу кінного ринку, за допомогою якого Е. Бем-Баверк пояснював "освіта цін при обопільній суперництві". [16] На ринку зустрічаються 10 потенційних покупців і 8 продавців коней. Їх оцінки, тобто ціни попиту та пропозиції (у Флоріна), такі:
| Покупці | Продавці | ||
| A1 | 300 | B1 | 100 |
| A2 | 280 | B2 | 110 |
| A3 | 260 | B3 | 150 |
| A4 | 240 | B4 | 170 |
| A5 | 220 | B5 | 200 |
| A6 | 210 | B6 | 215 |
| A7 | 200 | B7 | 250 |
| A8 | 180 | B8 | 260 |
| A9 | 170 | ||
| A10 | 180 | ||
Після деяких міркувань Е. Бем-Баверк приходить до висновку: " У мінову операцію фактично вступає з того і з іншого боку стільки осіб, скільки виходить пар, якщо розмістити попарно охочих купити і продати за ступенем їх обменоспособності у спадному порядку, - пар, з яких в кожній покупець оцінює товар, по відношенню віддається в обмін на нього речі, вище, ніж продавець ". [17]
Інакше кажучи, в мінову операцію фактично вступить 5 пар продавців і покупців, а ціна встановиться на рівні між 210 і 215 флоринів. Або, користуючись мовою оригіналу, "кордону (цени. - В. Г., С. І., В. М.) визначаються зверху оцінками останнього з фактично вступають у мінову операцію покупців і найбільш сильного за своєю обменоспособності з усунених конкуренцією з ринку продавців, а знизу- оцінками найменш сильного по обменоспособності з фактично укладають мінову операцію продавців і найбільш сильного по обменоспособності з не мають можливості вступити в мінову операцію покупців ". [18] 210 і 215 флоринів-це саме оцінки найбільш" сильних за своєю обменоспособності "з таких не вступили в угоду продавців і покупців.
Тепер визначимо рівноважну ціну згідно (2А.17). Попередньо зробимо безліч оцінок продавців (В) кількісно еквівалентним безлічі оцінок покупців (А). Для цього приймемо оцінки двох відсутніх на ринку продавців В9, В10 рівними оо - збільшити пропозицію понад 8 коней неможливо при будь-якому мислимому рівні цін пропозиції. Об'єднаємо всі 20 оцінок в один неубутною ряд від В1=100 до В10=оо. Медіана цього ряду лежить між 10-й і 11-й оцінкою , тобто 210
| Покупці | Продавці | ||
| A6 | 210 | B6 | 100 |
| A7 | 200 | A5 | 110 |
| B5 | 200 | A4 | 150 |
| A8 | 180 | B7 | 170 |
| A9 | 170 | A3 | 200 |
| B4 | 170 | B8 | 215 |
| A3 | 150 | A2 | 250 |
| A10 | 150 | A1 | 260 |
| B2 | 110 | B9 | ? |
| B1 | 100 | B10 | ? |
В такому випадку рівноважна ціна залишиться рівною медіані 210 <р * <215, але жодна пара фактично не вступить в угоду (рис. 2.11 , б). [19]
Якщо рівень рівноважної ціни визначається медіаною упорядкованого ряду цін попиту та пропозиції, то розміри надлишку покупців і продавців залежать від співвідношення медіани і середньої арифметичної того ж ряду.
Розглянемо останню залежність, помітивши попередньо, що р * є медіаною не тільки сукупності оцінок pi? Р=PD? PS, але і тих з них, які задовольняють вимогу (2А.14).
Тому обмежимося лише тими одиницями товару, в яких різниця між ціною попиту та пропозиції неотрицательна. [20]
Очевидно, що в цьому випадку розміри надлишку покупців і продавців залежать від розташування цін попиту та пропозиції щодо серединної величини ряду (медіани), тобто від характеристики кривої їх розподілу.
При симетричному розподілі, яке характеризується рівністю медіани і середньої арифметичної (), надлишок покупців буде дорівнює надлишку продавців, оскільки сума відхилень від середньої арифметичної дорівнює нулю і, отже, відхилення в одну сторону врівноважуються відхиленнями в іншу.
Таким чином, при р *=Me (pi)=
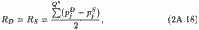
де RD - надлишок покупців; RS - надлишок продавців.
При асиметричному розподілі в складі сумарного надлишку можна виділити
![]()
Залишилося частина суспільної вигоди розподілиться між покупцями і продавцями порівну, як і при симетричному розподілі. Тому в загальному випадку розміри надлишку покупців і продавців складуть:

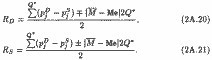
Знак в (2А.20) і (2А.21) залежить від характеру асиметрії. При лівосторонньої асиметрії, коли Me <, знак в (2А.20) позитивний, а в (2А.21) негативний, тобто надлишок покупців більше з- лішка_продавцов. Навпаки, при правобічної асиметрії, коли Me>, надлишок продавців перевищує надлишок покупців, відповідно знаки в (2А.20) і (2А.21) змінюються на зворотні. Нарешті, при крайній асиметрії, коли медіана збігається зі Всіма членами лівої чи правої половини ряду, вся вигода реалізується у покупців або продавців. Сказане справедливо лише в тому загальному випадку, коли медіана і, отже, рівноважна ціна визначаються однозначно (2А.16). Якщо ж однозначне визначення медіани неможливо, то, як вже зазначалося, рівноважна ціна може приймати будь-яке значення в межах медіанного інтервалу і, значить, сформулювати яку-небудь об'єктивну і точне правило визначення надлишків покупця і продавця неможливо.
Використовуємо тепер (2А.20) і (2А.21) для визначення надлишків на кінному ринку Е. Бем-Баверка. Але спочатку позбудемося (для визначеності) від медіанного інтервалу 210
| Оцінки покупців |
Оцінки продавців |
Різниця оцінок (A - B) |
||
| A1 | 300 | B1 | 100 | 200 |
| A2 | 280 | B2 | 110 | 170 |
| A3 | 260 | B3 | 160 | 110 |
| A4 | 240 | B4 | 170 | 70 |
| A5 | 220 | B5 | 200 | 20 |
| A6 | 210 | B6 | 210 | 0 |
| Всього | 1510 | 940 | 570 | |
Середня арифметична всіх 12 оцінок=(1510 + 940) / 2==204, 166 ..., медіана Me=210. Оскільки Me>, згідно (2А.20) і (2А. 21) маємо:
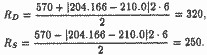
Перевірте результат прямим розрахунком величини надлишку для кожного з 6 покупців і 6 продавців, фактично вступили в угоду.
ПРИМІТКИ
[13] Думка про ринкову ціну як суб'єктивної середньої, отриманої "з ряду зроблених спостережень, зроблених над різними одиницями", була висловлена П. Б. Струве (Струве П. Б. Господарство і ціна. СПб.: М., 1913 . Ч. 1. С. 91-95).
[14] "Вся економічна діяльність всякого господарюючого суб'єкта прагне отримати більшу за менший, прагне до реалізації позитивних ціннісних різниць" (Струве П. Б. Господарство і ціна. М., 1916. Ч. 2. С. 22).
[15] Поверніться до визначення суспільної вигоди в 2.8 (рис. 2.24) як суми двох трикутників і як суми трапецій.
[16] Бем-Баверк Є. Основи теорії цінності господарських благ / / Австрійська школа в політичній економії. М., 1992. С. 370.
[17] Там же. С. 376.
[18] Там же. С. 377.
[19] Цікаво, що, перераховуючи властивості ціни як рівнодіюча існуючих в суспільстві оцінок, Бем-Ваверк фактично перераховує відомі властивості медіани як центральної величини ряду (Бем-Баверк Є. Основи теорії цінності господарських благ. С. 380-383). Інший аналіз кінного ринку Бем-Баверка, що приводить до тих же висновків, см.: Нейман Дж. фон, Мореенштерн О. Теорія ігор і економічна поведінка. М., 1970. С. 562-566.
[20] Бем-Баверк Є. Основи теорії цінності господарських благ. С. 380-383.
Інформація, релевантна "Додаток 2А. Ціна як статистична характеристика ринку"
- РЕЗЮМЕ
статистичні показники. Сучасна система міжнародної статистики є складним механізмом, в якому одні статистичні організації розробляють статистичну методологію, програми спостереження, а інші безпосередньо здійснюють збір, обробку та публікацію статистичних даних. Різноманіття статистичних збірників, що випускаються різними організаціями з різних сфер - Додаток 1 Основні характеристики федерального бюджету за період з 2004 по 2009 р., млрд. руб.
характеристики федерального бюджету за період з 2004 по 2009 р., млрд. руб. Джерело: Федеральні закони про виконання федерального бюджету за відповідний - Додаток 2 Крива Філіпса
ціна товару змінюється залежно від співвідношення попиту та пропозиції і що ці зміни тим значніше, чим більше тиск надлишкового попиту. Філліпс дав статистичну інтерпретацію цього положення стосовно ринку робочої сили для конкретного періоду і конкретної країни. Але й тут він не був новатором. У 1926 р. І. Фішер показав наявність аналогічної статистичної залежності між - Додаток. Інтерпретація графіків
додатки - навчити вас інтерпретувати і використовувати графіки, з якими вивстретітесь в цьому посібнику та в - Терміни і поняття
ціна «Ціна статі» і «ціна стелі» Ціна попиту і ціна пропозиції Економічна цінність Вартість Корисність Парадокс цінності «Ножиці цін» А. - Терміни і поняття
ціна «Ціна статі» і «ціна стелі» Ціна попиту і ціна пропозиції Економічна цінність Вартість Корисність Парадокс цінності «Ножиці цін» А. - Додаток 2 Крива Філіпса
ціна товару змінюється залежно від співвідношення попиту та пропозиції і що ці зміни тим значніше, чим більше тиск надлишкового попиту. Філліпс дав статистичну інтерпретацію цього положення стосовно ринку робочої сили для конкретного періоду і конкретної країни. Але й тут він не був новатором. У 1926 р. І. Фішер показав наявність аналогічної статистичної залежності між - Додаток
Додаток - Додаток
Додаток - Додаток
Додаток - Додаток
Додаток - Додаток
Додаток