8.5 Нова теорія витрат
Криві короткострокових витрат, представлені на рис. 8.5, характерні для тих виробництв, в яких зростаюча віддача змінного ресурсу змінюється спадної (рис. 7.8). Однак ми пам'ятаємо (див. 7.2.2), що у виробництвах, де постійний ресурс ділимо і однорідний, так що частина його може бути переведена в резерв або виведена з нього, спостерігається постійна віддача змінного ресурсу. Як зміниться поведінка витрат у тому випадку, якщо стадії спадної віддачі змінного ресурсу передує стадія постійної віддачі, в межах якої лінії середнього (АР) і граничного (МР) продукту зливаються, як було показано на рис. 7.9?
У цьому випадку криві загальних і змінних витрат, STC і SVC (як і крива загального продукту на рис. 7.9), починаються з прямолінійної ділянки (АВ і ОВГ на рис. 8.10).
Це означає, що аж до досягнення обсягу виробництва Q1 загальні та змінні витрати збільшуються пропорційно зростанню випуску.
Цьому ділянці в нижній частині рис. 8.10 відповідає лінія А'В ', паралельна осі випуску і представляє одночасно і частина кривої середніх змінних, і частина кривої граничних витрат, SAVC=SMC.
Ця ділянка відповідає ділянці МР=АР на рис. 7.9.
І лише при більш високих, ніж Q1, обсягах виробництва криві SAVC і SMC набувають традиційну, як на рис. 8.5, конфігурацію.
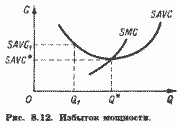
Якщо ділянка постійної віддачі змінного ресурсу лежить між зонами зростаючій і зменшення віддачі, крива короткострокових середніх змінних витрат, SAVC, набуває блюдцеобразную форму, а плоске дно блюдця характеризується рівністю SAVC і SMC (рис. 8.11).
Лівіше цієї ділянки середні змінні витрати зі зростанням виробництва падають, правіше - зростають.
На думку багатьох економістів, криві середніх та граничних витрат, представлені на рис. 8.10 і 8.11, краще відображають їх реальну поведінку, ніж ті, що пропонуються традиційної теорією.
Наявність широкого плоского дна дає можливість підприємству мати певний резерв потужності, що дозволяє гнучко реагувати на зміну ринкових умов, варіювати обсяг випуску у відповідь на відповідні зміни попиту при незмінному рівні середніх змінних витрат.
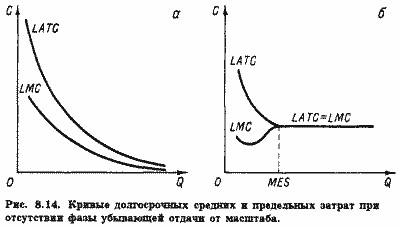
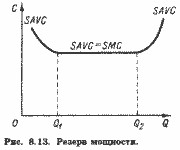
Традиційна теорія припускає, що в короткому періоді підприємство може змінювати рівень використання виробничої потужності, але не саму потужність. При цьому оптимальний (з точки зору мінімуму середніх змінних витрат) обсяг - Q * на рис. 8.12. Якщо за умовами попиту випуск повинен бути менше, скажімо Q1, то виникає невикористовуваний надлишок потужності (Q * Q1i), а середні змінні виявляються вище (SAVC1> SAVC *). Нова теорія витрат виходить з того, що ділянка Q1Q2 (рис. 8.13) характеризує запланований резерв потужності, який може використовуватися або не використовуватися без зміни середніх змінних витрат. Наявність такого заздалегідь вбудованого резерву потужності надає підприємству певне поле для маневру.
У тривалому періоді, як ми знаємо, всі витрати підприємства мають змінний характер. Звичайно передбачається, що довгострокові середні витрати знижуються до досягнення певного обсягу випуску, а потім зростають (рис. 8.9).
Однак нова теорія витрат передбачає можливість іншої, відмінної від представленої на рис. 8.9, конфігурації кривої LATC. Ми пам'ятаємо, що права, висхідна вгору її частина пов'язана з наявністю неекономічності від масштабу, яка обумовлена перш за все зростанням управлінських витрат.
Прихильники нової теорії витрат пропонують більш тонкий аналіз. Виробничі витрати, вважають вони, безперервно знижуються із збільшенням масштабу виробництва, тоді як управлінські можуть при досягненні певного масштабу збільшуватися.
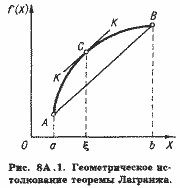
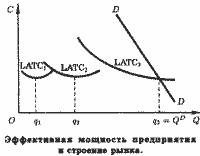
Тому конфігурація кривих LATC залежить від того, перекриває чи зниження виробничих витрат зростання управлінських або не перекриває. Якщо зниження виробничих витрат з надлишком перекриває збільшення управлінських, криві LATC і LMC будуть мати конфігурацію, представлену на рис.
Більшість економістів згодні в тому, що середні витрати в тривалому періоді, що включають витрати на виробництво, управління, маркетинг, збут і т.п., із зростанням масштабу виробництва знижуються, принаймні до досягнення підприємством (або окремої його одиницею) певного розміру. Розбіжності ж стосуються того, як поведуть себе витрати після того, як цей критичний розмір буде досягнутий, і чи завжди він існує. Дати будь-якої однозначну відповідь на це питання не можна. У різних виробництвах ми можемо спостерігати різні ситуації:
а) резерви економічності невичерпні, і LATC знижуються на всьому діапозоні можливого попиту (рис. 8.14, a);
б) після вичерпання резервів економічності LATC починають зростати (рис. 8.8; 8.9, а, б);
в) після вичерпання резервів економічності LATC стабілізуються на незмінному рівні (8.14, б);
г) стадія незмінного рівня LATC змінюється при досягненні певного масштабу стадією неекономічності (рис. 8.9, в).
Знання функцій витрат, як ми побачимо далі, вельми важливо для прийняття рішень як на рівні підприємств, так і на урядовому рівні. Функції короткострокових витрат мають ключове значення для визначення цін і обсягів випуску, тоді як функції довгострокових витрат важливі для планування розвитку підприємств та їх інвестиційної політики. Оцінка економічності від масштабу необхідна для проведення ефективної урядової політики регулювання ринку, перш за все щодо монополій і злиттів.
Додаток 8А. Середні витрати як середнє значення функції
Поняття середніх витрат і їх взаємозв'язок з граничними потребують додаткового обговорення. Важливо насамперед зрозуміти, що середні витрати зовсім не є якоюсь середньою з ряду незалежних випадкових величин. Якщо середні витрати при випуску 100 одиниць продукції становлять 1000 руб., То це зовсім не означає, що одна її одиниця обходиться, скажімо, в 800, інша в 1200 руб. і т.п. Насправді, коли ми говоримо про середні витратах, ми маємо на увазі середнє значення функції витрат від обсягу випуску.
Якщо яка-небудь функція f (x) неперервна і диференційовна в замкнутому проміжку (а, b), то, згідно теоремі Лагранжа, середнє її значення в цьому проміжку дорівнює значенню похідної f '(x) в деякій точці x, що лежить всередині даного проміжку:
[f (b) - f (a)] / (b - a)=f (x). (8А.1)
Для з'ясування геометричного сенсу теореми Лагранжа зауважимо, що ліва частина (8А.1) є кутовий коефіцієнт січної, що проходить через точки А (а, f (а)) і В (b, f (b)) кривої у=f (x), a права частина є кутовий коефіцієнт дотичної до тієї ж кривої в точці С (x, f (x)).
Теорема Лагранжа про середнє значення функції стверджує, що на кривій у=f (x) між точками А і В завжди знайдеться така точка С, дотична до якої паралельна січної АВ (рис. 8А.1) .
Використовуємо тепер теорему Лагранжа для визначення середніх змінних витрат.
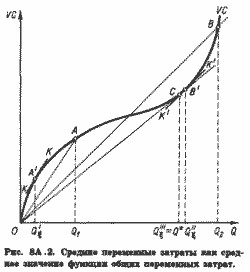
На підставі (8А.1) ми можемо стверджувати, що середні змінні витрати при випуску Qi, тобто в інтервалі (Q0, Qi), дорівнюють граничним витратам при деякому невизначеному обсязі випуску Qx, причому Q0? Qx? Q1, т. e.
AVC (Q0, Qi)=[VC (Qi) - VC (Q0)] / (Qi - Q0)=VC (Qx)=MC (Qx), (8A.2)
при цьому Qx? Qi. Як виявляється з рис. 8А.2,
AVC (Q1)=MC (Qx) Qx
До тих же висновків можна прийти і на основі формули кінцевих збільшень:
VC (Q0 + DQ) - VC (Q0)=VC (Qx) DQ, (8А.
або на основі теореми про середню інтегрального числення, згідно з якою певний інтеграл дорівнює добутку довжини проміжку інтегрування на значення підінтегральної функції в деякій точці всередині цього проміжку .
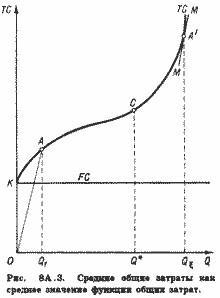
Розглянемо тепер середні загальні витрати. Середнє значення функції загальних витрат TC (Q) складе:
ATC (Q0, Qi)=[TC (Qi) - TC (Q0)] / (Qi - Q0)=TC (Qx)=MC (Qx), (8A.5)
При всій схожості (8А.2) і (8А.5) звернемо увагу і на важливу відмінність.
Для середніх загальних витрат.
Зупинимося на разі, коли Qx> Qi. Зауважимо, що, оскільки ТС=FC + VC, крива ТС на рис. 8А.З включає і сегмент ОК - FC, тобто має правобічний межа.
Тому на дузі КА не знайдеться точки, дотична в якій була б паралельна променю ОА. Але така точка (А1) знайдеться значно правіше точки А, так що в даному випадку Qx> Q1.
Зауважимо, що в міру зміщення точки А вправо точка А 'буде зміщуватися вліво, поки їх взаємне розташування відносно точки С, в якій ATC (Q *)=MC (Q *), не зміниться на протилежне.
Ці залежності легко простежити в табл. 8А.1, зіставляючи послідовно значення МС з AVС та АТС.
Зокрема, можна переконатися, що:
AVC (Qi) »MC (Qj), (8А.6)
Qi> Qj для всіх i, j 6;
ATC (Qi) »MC (Qj), (8А.7)
Qi
Qi> Qj для всіх i> 11, j <11,
Qi=Qj для i, j=11,

Таблиця 8А.1 Розрахунок середніх і граничних витрат (грн.)
| Q | FC | VC | TC (2 +3) | AVC (3:1) | ATC (4:1) | MC - (TCQ - TCQ- 1) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 1 2 3 4 5 6 * 7 8 9 10 11 * 12 13 14 15 16 17 18 19 20 |
100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 |
- 10.00 16.00 21.00 26.00 30.00 36.00 45.50 56.00 72.00 90.00 109.00 130.40 160.00 198.20 249.50 324.00 418.50 539.00 698.00 900.00 |
100.00 110.00 116.00 121.00 126.00 130.00 136.00 145.50 156.00 172.00 190.00 209.00 230.00 260.00 298.20 349.50 424.00 518.50 639.00 798.00 1000.00 |
- 10.00 8.00 7.00 6.00 6.00 6.00 * 6.50 7.00 8.00 9.00 9.91 10.87 12.31 14.61 16.69 20.25 24.62 29.94 36.74 45.00 |
- 110.00 58.00 40.38 31.50 26.00 22.67 20.78 19.50 19.10 19.00 19.00 * 19.20 20.00 21.30 23.30 26.50 30.50 35.50 42.00 50.00 |
- 10.00 6.00 5.00 5.00 4.00 6.00 * 9.50 10.50 16.00 18.00 19.00 * 21.40 29.60 38.20 51.30 74.50 94.50 120.50 159.00 202.00 |
Звернемо також увагу на те, що середнє значення функції, або середні витрати, є зазвичай фіктивною, лічильної середньої; вони можуть збігатися, а можуть і не збігатися ні з одним значенням граничних. [1] Тому рівності (8А.6) і (8А.7) виконуються зазвичай лише як наближені, в тому числі і для Q *.
ПРИМІТКА
[1] K середнім рахунковим, або фіктивним, відносяться ті середні, значення яких не зустрічається в даній сукупності, тоді як реальна, або дійсна, середня відповідає хоча б одному з її членів. Прикладом фіктивною, або лічильної, середньої є середня арифметична трьох чисел - 1, 2, 6. Вона дорівнює 3 і не збігається ні з одним з цих чисел (Джині К. Середні величини. М., 1970. С. 64).
Інформація, релевантна " 8.5 Нова теорія витрат "
- Глава 29 Дж.М. Кейнс: нова теорія для зміненого світу
нова теорія для зміненого - ГЛАВА 29 Дж.М. Кейнс: НОВА ТЕОРІЯ ДЛЯ зміниться СВІТУ
ГЛАВА 29 Дж.М. Кейнс: НОВА ТЕОРІЯ ДЛЯ зміниться - Ключові терміни
теорія вартості Відчуження працівників Соціалізм Комунізм Капіталізм Командна економіка Нова економічна політика (неп) Гіпотеза - ГЛАВА 34 «НОВА КЛАСИКА». ВІДНОВЛЕННЯ ТРАДИЦІЇ
нова класика », або« нова класична макроекономіка ». Як випливає з назви, йдеться про макроекономічну концепції, побудованої на основі і відповідно до неокласичної мікроекономічної моделлю. В області практики «нова класика» виступила з позицій, близьких монетаризму, довела до логічного кінця ідею про обмеженість впливу грошової політики на економіку, заявивши, що - ГЛАВА 38 НОВА інституціональної теорії
нова інституційна теорія ». Таке позначення може породити помилкове уявлення про її спорідненість зі «старим» інституціоналізмом Т. Веблена, Дж. Коммонса, Дж. Гелбрейта. Однак збіги тут скоріше чисто термінологічні (наприклад, поняття «угоди» є вихідною одиницею аналізу як для Дж. Коммонса, так і для «нових» институционалистов). Насправді коріння нової і - Глава 38 Нова інституціональна теорія
нова інституційна теорія ». Таке позначення може породити помилкове уявлення про її спорідненість зі «старим» інституціоналізмом Т. Веблена, Дж. Ком-Монса, Дж, Гелбрейта. Однак збіги тут скоріше чисто термінологічні (наприклад, поняття «угоди» (transaction) є вихідною одиницею аналізу як для Дж. Коммонса, так і для «але-лих» институционалистов). Насправді коріння - Глава 34 «Нова класика»: відновлення традиції
нова класика », або« нова класична макроекономіка ». Як випливає з назви, мова йде про макро-жономіческой концепції, побудованої на основі і відповідно ь неокласичної мікроекономічної моделлю. В області прак-[ики «нова класика» виступила з позицій, близьких монетаризму, довела до логічного кінця ідею про обмеженість впливу грошової політики на економіку, заявивши, що - У теорії, могла б нова світова валюта (пропозицію Росії на саміті "Великої двадцятки") якось вплинути на обстановку?
Нова світова валюта нічого б не змінила, хоча ця ідея залишається привабливою утопією. Криза породжений не проблемами в грошовому обігу. Якраз всі проблеми в обігу грошей виникли через кризу, суть якого в зниженні обігу товарів через слабкість - 6. ФОРМУВАННЯ неокласичної школи. А. МАРШАЛЛ. ДЖ. Б. КЛАРК
теорія добробуту ». Теорія граничної продуктивності праці і капіталу Дж. Б. Кларка. Концепція статики і динаміки. Становлення факторного - Терміни і поняття
нова теорія зростання) Концепція нульового економічного зростання Теорії стадій економічного зростання (К. Маркса і У. - Терміни і поняття
нова теорія зростання) Концепція нульового економічного зростання Теорії стадій економічного зростання (К. Маркса і У.