§ 4. Фондові індекси
Для розрахунку фондового індексу використовуються методи розрахунку середніх величин. З методичної точки зору індекси різняться:
по сукупності компаній, тобто переліку підприємств, акції яких включаються до розрахунку;
по виду застосовуваної середньої;
за способом визначення ваг в тому випадку, якщо застосовується зважена середня.
Звичайно як основного критерію для включення акції якої-небудь компанії в сукупність при розрахунку фондового індексу використовується торговельна активність по даній цінному папері, яка визначається по середній кількості здійснених угод за торговий день протягом досить тривалого періоду . При цьому в сукупність включаються ті акції, торговельна активність яких перевищує встановлений мінімальний рівень.
Дана сукупність може просто збігатися з лістингом біржі, оскільки критерій торгової активності застосовується і для включення до лістингу. Зокрема, сукупність акцій, за якою обчислюється зведений індекс Нью-Йоркської фондової біржі (NYSE Composite Index), складається з усіх котируються на цій біржі акцій (більше 1500).
Іншим критерієм є репрезентативність, З одного боку, в сукупність повинні входити акції компаній, що представляють основні галузі економіки (при цьому з'являється можливість розраховувати галузеві індекси), а з іншого - необхідно враховувати рівень цін, що складається на основних торгових майданчиках. Наприклад, сукупність, що складається з акцій 500 компаній, яка використовується для розрахунку індексу Standard & Poor's 500, утворюється шляхом вибірки акцій, що котируються на Нью-Йоркській фондовій біржі (NYSE), Американській фондовій біржі (АМЕХ) і в електронній системі позабіржового ринку Національної асоціації дилерів цінних паперів (NASD).
Зміна курсу акцій різних компаній відбувається в основному синхронно, тому уявлення про динаміку цін на ринку можна отримати на основі індексу, розрахованого по невеликій кількості акцій великих компаній, для яких характерна найбільш висока торговельна активність і які забезпечують істотну частку торгових оборотів. Класичним прикладом такого підходу, званого в статистиці методом основного масиву, є розрахунок найбільш відомого середнього промислового індексу Доу-Джонса (DJIA-Dow Jones Industrial Average), публикуемого з 1898 р. Він розраховується за сукупністю, що складається всього з 30 акцій найбільш великих компаній, котируються на Нью-Йоркській фондовій біржі. Спочатку індекс Доу-Джонса розраховувався за акціями 12 компаній. У 1916р. число компаній збільшилася до 20 і в 1928 р. - до 30. Природно, за цей значний проміжок часу склад сукупності не міг залишатися незмінним. Акції компаній, які зазнали реорганізації або банкрутства, а також зазнавали значне зниження торгової активності, замінялися акціями інших компаній, що відрізнялися високою торговою активністю і збільшеними торговими оборотами. Проведення такої ротації сукупності супроводжується спеціальною процедурою зміни розрахунку індексу, яка забезпечує його сумісність з попередніми значеннями.
Вид застосовуваної середньої залежить тому, як утворюється обсяг сукупності. Як правило, це відбувається шляхом підсумовування, тому найбільш часто використовується середня арифметична. При цьому одночасно встановлюється, чи буде середня простий або зваженої і, якщо зваженої, то що повинно виконувати роль ваг.
Індекси S & P і NYSE Composite розраховуються на основі середньої арифметичної зваженої. Як терезів виступають обсяги ринкової капіталізації (твір ринкової ціни на кількість акцій в обігу) по кожній компанії. Розрахунок проводиться за формулою, аналогічною формулою індексу цін Ласпейреса, яка, як відомо, може бути представлена у вигляді середньої арифметичної індивідуальних індексів, зважених за вартісними обсягами базисного моменту. При цьому враховується основна перевага індексу цін Ласпейреса, яке полягає в тому, що він задовольняє умові транзитивності за часом, тобто твір ланцюгових індексів дорівнює базисному індексу.
Індекси, зважені за обсягами ринкової капіталізації, можна представити в наступному вигляді:
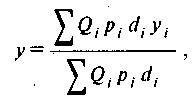
де pt і p0 - ціна акції відповідно в момент t і в базисний момент;
Q0 - кількість акцій в обігу;
I0 - початкове значення індексу. (Для S & P 500 базисний момент - кінець 1943 р., початкове значення - 10; для індексу NYSE Composite базисний момент - 1965
Якщо розділити цей індекс на початкове значення / 0, то результат буде показувати, скільки раз зросла сумарна ринкова капіталізація розглянутої сукупності компаній у порівнянні з базисним моментом. По-іншому цей результат можна інтерпретувати як середнє відносне зміна цін на акції.
За аналогічною формулою розраховується індекс російського позабіржового ринку акцій корпоративних підприємств - індекс РТС (Російської торгової системи), а також індекси АК & М і ASP (агентство «Скейт-Пресс»). Якщо початкове значення індексу РТС одно 100 і зафіксовано на 1 вересня 1995 р., то його поточне значення трактується як середній базисний темп зростання цін на акції підприємств, включених в сукупність *.
Індекс РТС розраховується один раз на годину. Значення індексу на конкретну дату встановлюється за результатами його розрахунку на 18.00 (момент офіційного закінчення торгового дня в РТС). Для розрахунку використовуються середні ціни угод за попередні 24 ч. У тому випадку, коли угоди не проводилися, в якості ціни приймається середина спреду (інтервалу між максимальною котируванням на купівлю та мінімальної котируванням на продаж) на розрахунковий момент.
Змінена формула, в якій безпосередньо враховується властивість транзитивності за часом, виглядає наступним чином:
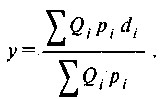
Якщо цю формулу представити у вигляді:
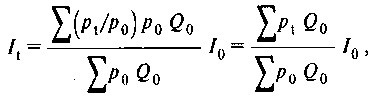
то можна помітити, що розрахунок індексу змінився в результаті додавання множника (коефіцієнта змикання), що представляє собою співвідношення обсягів капіталізації за новим і колишнього складу сукупності на момент t-1.
Слід зазначити, що застосовується при розрахунку деяких російських фондових індексів усереднення за будь-який попередній інтервал часу виставляються котирувань або цін укладених угод («за останні 24 години» або «протягом торгового дня") не зовсім відповідає природі вимірюваного явища. Ціна акції є моментной величиною, в той час як середня за проміжок часу - величиною інтервального. У результаті індекс, розрахований на основі інтервальних середніх цін, володіє ефектом запізнювання, який особливо відчувається при різких змінах цін.
Зовсім іншу природу має індекс Доу-Джонса, який розраховується як проста середня цін акцій 30 компаній, включених в сукупність. Своєрідність розрахунку полягає в особливій процедурі, що дозволяє дотримуватися умова порівнянності при змінах сукупності з причини її ротації або дроблення акцій, що входять до її складу. Сума цін акцій поділяється не на їх кількість, що повністю відповідало б простої середньої арифметичної, а на попередньо розрахований дільник.
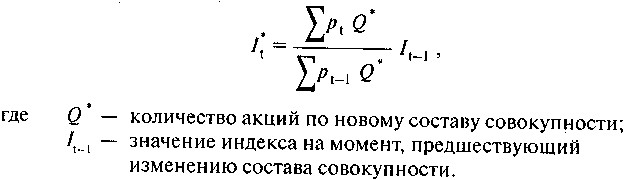
Доу-Джонса розраховується як відношення суми поточних цін акцій щодо нового складу сукупності до нового делителю. По суті справи, це один з добре відомих прийомів приведення часового ряду в порівнянний вид. Однак ця порівнянність з часом набуває все більш умовний характер.
Основним недоліком індексів, що обчислюються виходячи з середньої ціни (типу індексу Доу-Джонса), є нічим не обгрунтована більш висока чутливість до змін цін акцій, що мають більш високу абсолютну величину. Припустимо, що значення такого індексу за сукупністю, що складається всього з двох акцій з цінами в початковий момент 10 і 1 дол. США, становить: (10 + 1) / 2=5,5. До поточного моменту ціна першої акції зросла на 10%, а другий - знизилася на 10%. Вартість портфеля інвестора, що вклав в початковий момент однакову кількість грошей в першу і другу акції, не змінилася. У той же час індекс виріс на 8,2% [(11 + 0,9) / 2=5,95 і (5,95 / 5,5 - 1) 100%=8,2%]. Отже, такі індекси можуть адекватно відображати зміни ринку лише тоді, коли абсолютні величини цін акцій, включених у сукупність, мало відрізняються один від одного.
Якщо просту середню застосовувати не для власне цін на акції, а для їх індивідуальних індексів (тобто p1/p0), то переважно використовувати формулу середньої геометричної, а не середньої арифметичної, оскільки вона не задовольняє умові транзитивності:
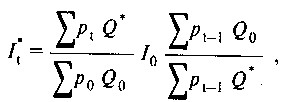
У той час як формула середньої геометричної цій умові задовольняє:

.
Як приклади фондових індексів, які розраховуються за формулою простої геометричної середньої, можна навести індекс VLA (Value Line Average), що розраховується компанією Arnold Bernhard & Со. з 1961 р., а також індекс SOBI, що розраховується Російським консультаційним агентством «Соболєв».
Фондові індекси, як правило, використовуються для визначення відносного рівня цін на ринку і оцінки їх динаміки, тому абсолютне значення індексу не представляє особливого інтересу. Набагато важливіше визначити, як його значення змінюється щодо попередніх значень. З цієї точки зору різні коректно побудовані індекси дають приблизно однакові результати. Зміна цін більшості найбільш ліквідних акцій відбувається досить синхронно, тому по відносно невеликій кількості акцій з високим рівнем торговельної активності можна визначити динаміку цін на ринку. На рис. 18.1 наведено графік динаміки індексу РТС та індексу акцій п'яти компаній (РАО ЄЕС, ЛУКойл, Мосенерго, Норільський нікель і Ростелеком), розрахованого за формулою простої середньої геометричної, з якого видно, що відносна динаміка обох індексів розрізняється досить незначно.
Рис. 18.1. Графік динаміки індексу РТС і індексу акцій п'яти компаній
Для оцінки співвідношення динаміки цін якої-небудь акції і динаміки цін на ринку в цілому використовуються альфа-і бета-коефіцієнти, які розраховуються за рівнянням лінійної регресії. В якості залежної змінної у приймається ряд ланцюгових темпів приросту ціни на конкретну акцію, а в якості незалежної змінної х - ряд ланцюгових темпів приросту фондового індексу:
у=? +? Х +?.
Коефіцієнт? показує, в якому співвідношенні знаходяться зміна ціни конкретної акції і зміна рівня цін на ринку в цілому. Якщо? позитивна, то це означає, що ціна на дану акцію в середньому зростає швидше (знижується повільніше), ніж ціни на ринку в цілому. Іншими словами, за розглянутий період спостерігався підвищений попит на цю акцію, яка раніше була відносно недооцінена.
Таблиця 18, Коефіцієнти зміни цін на акції щодо зміни
індексу РТС
(за період з 27 березня 1996 р. по 35 березня 1997 р.)
| ( | ( | R2 | |
| РАО ЄЕС | 0,303 | 0,854 | 0,567 |
| ЛУКойл | 0,076 | 0,670 | 0,593 |
| Мосенерго | 0,257 | 0,814 | 0,496 |
| Норільський нікель | -0,281 | 0,736 | 0,545 |
| Ростелеком | 0,186 | 0,762 | 0,453 |
| Торговий дім ГУМ | 0,349 | 0,468 | 0,154 |
Коефіцієнт? характеризує залежність динаміки цін конкретної акції від динаміки цін на ринку. Чим більше?, Тим більшою мірою ціна даної акції реагує на зміну цін на ринку в цілому. Таким чином, коефіцієнт р відображає порівняльну ступінь ризику інвестицій в дану акцію.
Коефіцієнт детермінації R2 показує, якою мірою ціна конкретної акції залежить від цін на ринку в цілому.
Контрольні питання
I. Є такі дані по ГКО з різними термінами погашення: Визначте значення індексу ДКО на 29 грудня 1995 р. і на 29 ап
| До 1 міс. | Від 1 до 2 міс. | Від 2 до 3 міс. | Понад 3 міс. | |
| 29.12.Доля в загальному ринковому обсязі паперів в обігу Прибутковість Дюрація |
19,9% 97% 11 |
29,2% 110% 45 |
30,4% 10% 6 |
20,5% 04% 133 |
| 29.04.Доля в загальному ринковому обсязі паперів в обігу Прибутковість Дюрація |
22,6% 67% 12 |
18,8% 66% 45 |
17,1% 108% |
41,5% 144% 137 |
реля 1996 Оцініть вплив структурного фактора на його зміну.
2. Індекс РТС 12 листопада 1996 становив 190,2 при обсязі торгів 29,736 млн. дол., А 27 лютого 1997 - 337,38 при обсязі торгів 44,081 млн. дол. Визначте, як змінилася кількість проданих акцій.
3. Оцініть ринкові властивості акцій на основі табл. 18.1.
Література
1. Игнатущенко В., Шитов В. Державні облігації. - М.: ИНФРА, 1996.
2. Миркин Я. Цінні папери та фондовий ринок. - М.: Перспектива, 1995.
3. Ованесов А., Гулий А. Який ринок - такий і індекс; Кулакова І., Ч іхачев Н. Кому він потрібен, цей індекс? / / Ринок цінних паперів. № 24. 1996.
Інформація, релевантна "§ 4. Фондових індексів"
- Тримає руку на пульсі РИНКУ
фондів закритого типу та установ, 262 займаються інвестиціями в нерухомість, умови спільного ринку не грають великої ролі в русі акції. Завдяки своїй стійкості, ці нізковолатільние ринки не піддаються прямому впливу широких коливань ринку в цілому. Якщо Доу підвищився або впав на 100 пунктів, багато з цих нізковолатільних цінних паперів можуть не просунутися навіть і на 1/8. - Питання 61 Біржові індекси
фондових біржах РФ. З 1998 по 2006 р. розраховувався MISEX Composite Index (або індекс RMX) - спільний індекс ММВБ і телеграфного агентства «Рейтер» (Reuters). Значення індексу обчислювалося за даними роботи трьох торгових майданчиків - ММВБ, РТС і Московській фондовій біржі - ВВП І ЗАГАЛЬНИЙ РІВЕНЬ ЦІН
індексів. Принципова модель цінового індексу: Існує безліч цінових індексів, найбільш загальним з них є дефлятор - ВІДСТЕЖЕННЯ NASDAQ-КОМПОЗИТ
індексу. Він надзвичайно волатильним і схильний до захоплюючих дух підйомів і спустошливим розпродажів за зниженими цінами, навіть коли Індекси Доу і S & P залишаються - 1.5. Макроекономічні показники рівня цін
індекси цін. Вони призначені для визначення середнього зміни цін в економіці. Всі індекси цін описують зміна вартості репрезентативного набору (кошика) товарів, зважене за кількістю кожного товару. Види індексів цін: - індекс оптових цін (на всі товари, що реалізуються великими партіями); - індекс цін виробників (оптових цін на товари окремих галузей); - індекс - Значить, ви переконані, що «коригування» відбуватимуться одна за одною?
фондових ринках. 5 лютого потужний овал стався на американських і європейських біржах. Потім настало чергове заспокоєння і нове падіння 17 березня. На Лондонській фондовій біржі 5 лютого сукупна вартість котируються акцій скоротилася на 2,63%. На Франкфуртській біржі падіння склало 3,36%, на Брюссельської - 3,17%, на Міланській -3,07%, на Амстердамської - 3,34%. У Парижі папери подешевшали - Терміни і поняття
індекси Рейтингові оцінки облігацій Єврооблігація Фінансова - Біржові індекси
фондова біржа. Індекс курсової ціни кожної акції (облігації) визначається як добуток її курсу на число акцій цього типу, що котируються на біржі, поділене на номінал акції. Надалі індекси курсових цін акцій використовуються для розрахунку агрегованого біржового індексу. Найбільш поширеним серед них вважається індекс Доу Джонса (Dow Jones, DJ) Нью-йоркській фондовій біржі. За його - Терміни і поняття
Інфляція Інфляція попиту Інфляція витрат Дефлятор ВВП Індекс цін Індекси Ласпейреса, Пааше і Фішера Повзуча інфляція Галопуюча інфляція Гіперінфляція «Імпортується» інфляція Інфляційні очікування Дефляційна - 2. Вимірювання і показники інфляції
індекси цін, у тому числі індекси цін в споживчому секторі - § 3. ЕКОНОМІЧНА ОЦІНКА ОСНОВНИХ ФОНДІВ
фондів в натурі необхідні для знання їх технічного стану пооб'єктно і розрахунків виробничої потужності з усіма витікаючими з цього подальшими операціями по них. Такий облік з відповідною оцінкою стану основних фондів здійснюється в бухгалтерії і в технічних службах. Економічна оцінка основних фондів здійснюється за первісною, відновною та залишковою - 6. Як читати біржові індекси, котирування і рейтингові оцінки
індекси і котирування) залишається досить точним індикатором стану справ у