4.4 Еластичність попиту по доходу
Еластичність попиту по доходу характеризує відносну зміну попиту на який-небудь товар в результаті зміни доходу споживача. Коефіцієнтом еластичності попиту по доходу називають відношення відносної зміни обсягу попиту на i-тий товар до відносного зміни доходу споживача:
Якщо ej <0, товар є низькоякісним, збільшення доходу супроводжується падінням попиту на цей товар.
Якщо e I> 0, товар називається нормальним, із зростанням доходу збільшується і попит на цей товар.
Серед нормальних товарів можна виділити три групи. Товари першої необхідності, попит. На які зростає повільніше зростання доходів (0
4.5 Зв'язок між еластичністю попиту, зміною ціни і виручкою продавця (витратами покупця)
На основі кривої попиту можна визначити витрати покупців на придбання даного товару, які формують виручку продавців (TR; total revenue - англ.):
TR=PQ. (4.11)
При зниженні ціни з P 1 до P 2 обсяг попиту збільшиться з Q 1 до Q 1 v (рис. 4. 8). Але що станеться при цьому із загальною виручкою продавців або витратами покупців?
Зростуть вони чи знизяться? І на скільки? При ціні P 1 загальна виручка складе TR=OP1 AQ 1, при ціні P 2 - TR=OP 2 BQ 2. Оскільки частина виручки дорівнює площі прямокутника OP 2 CQ 1, її зміна при зниженні ціни з P 1 P 1 до P 2 складе, як очевидно:
?? TR=Q 1 P - P 2?? Q,
або:
?? TR=Q 1?? P (1 - P 2?? Q / Q 1 P) (4.12)
Оскільки вираз P 2?? Q / Q 1?? P представляє коефіцієнт прямої еластичності попиту за ціною, розрахований на базі мінімальних значень об'єму і ціни, ми можемо переписати (4.12) так:
?? TR=Q 1?? P (1 - ei). (4.13)
Очевидно, що зміна загальної виручки (?? TR) залежатиме при даному обсязі попиту (продажів) від зміни ціни (?? P) і еластичності попиту. Відповідні залежності наведені нижче:
| Зміна ціни | ei> 1 | ei=1 | ei <1 |
| ? P> 0 | ? TR <0 | ? TR=0 | ? TR> 0 |
| ? P <0 | ? TR > 0 | ? TR=0 | ? TR <0 |
Як бачимо, у випадку еластичного попиту саме зниження ціни веде до збільшення виручки продавців, тоді як при нееластичним попиті зростання виручки обумовлений підвищенням ціни. Це положення досить важливо при визначенні політики цін як на рівні окремих фірм, так і на рівні держави.

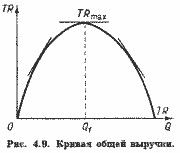
Повернемося тепер до рис. 4.3. При русі вздовж кривої попиту від точки D до точки D 'зниження ціни буде супроводжуватися і зменшенням коефіцієнта еластичності від?? до 0. Отже, згідно (4.11), ми можемо укласти, що спочатку загальна виручка продавців буде зростати - у точці Е, де е=1, вона досягне максимуму; потім вона знижуватиметься. Таким чином, як показано на рис.4.9, крива загальної виручки при лінійної функції попиту (рис. 4.2, 4.3, 4.8) має куполоподібну форму.
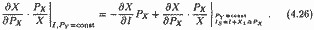
Приріст загальної виручки в результаті продажу додаткової одиниці називають граничною виручкою (MR; marginal revenue - англ.). Легко переконатися в тому, що за будь (позитивному) обсязі продажів MR <Р. Оскільки весь зрослий на одиницю обсяг продукції (Q n +1) буде проданий за нижчою ціною, ніж обсяг Q n гранична виручка дорівнюватиме ціні додатково проданої одиниці мінус втрати у виручці, обумовлені продажем всіх "попередніх" Q n одиниць за нижчою ціною: MR n +1=P n +1 - (P n - P n +1) Q n. (4.14)
Оскільки P n - P n +1> 0, MR n +1
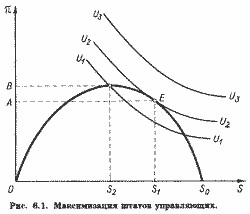
Графічно криву граничної виручки можна побудувати на основі кривої попиту.
Виберемо на кривій попиту довільну точку А (рис.4.10) і проведемо з неї перпендикуляри АР і AQ до осей координат. Відзначимо на АР точку С, таку, щоб PC=AC. Проведемо через неї промінь з точки В і відзначимо його перетин з AQ (точка В). Отриманий промінь і представляє лінію граничної виручки (MR).
Дійсно, при ціні Р загальна виручка дорівнює площі прямокутника OPAQ, тоді як сума граничної виручки від продажу всіх одиниць товару дорівнює площі трапеції ODBQ. Але обидві площі рівні, оскільки вони мають загальну частину OPCBQ, а трикутники DPC і АСВ рівні. Отже, DCB є лінія граничної виручки.
Гранична виручка може бути представлена і як перша похідна загальної виручки за кількістю даного товару:
MR=d (TR) / dQ=d (PQ) / dQ. (4.15)
Оскільки Р=f (Q), ми можемо записати:
MR=d (PQ) / dQ=P (dQ / dQ) + Q (dQ / dQ)=P + Q (dP / dQ). (4-16)
Оскільки ei=- (dQ / dP) (P / Q), ми можемо записати:
P / e IQ=dP / dQ. (4.17)
Підставляючи (4.17) в (4.16), отримаємо:
MR=P + Q (dP / dQ)=P v Q (P / ei Q)=PP / ei
або:
MR=P (1 - 1 / ei).
Звідси очевидно, що при ei=1 MR=0 і загальна виручка досягає максимуму (точка Q 1 на рис.4.9).
4.6 Деякі співвідношення між коефіцієнтами еластичності
Між коефіцієнтами еластичності існують певні співвідношення, що мають важливе теоретичне і практичне значення. Розглянемо деякі з них.
Нехай дано бюджетне обмеження:
PXX + PYY (4.19)
і функції попиту на товари X і Y:
X=DX (PX, PY, I)
Y=DX (PX, PY, I)
Диференціюючи (4.19) по доходу I, отримаємо:
PX (dX / dI) + PY (dY / dI) (4.20)
Помножимо перший доданок лівої частини (4.20) на одиницю (1=X / I - I / X), а другий на 1=Y / I - I / Y і перетворимо результат до вигляду:
(PXX / I) - (dX / dI) - (I / X) + (PYY / I) - (dY / dI) - (I / Y) (4.
Ми можемо інтерпретувати сомножители PXX / I і PYY / I в правій частині (4.21) як питомі ваги (у частках одиниці) витрат на покупку відповідно товарів X і Y в загальних витратах споживача I.
hX=PXX / I, hY=PYY / I. (4.22)
Очевидно, що:
(dX / dI) - (I / X)=eI, X, (dY / dI) - (I / Y)=eI, Y. (4.23)
Підставляючи (4.22) і (4.23) в (4.21), отримаємо:
hXeI, X + dYeI.Y=1. (4.24)
Це означає, що зважена сума коефіцієнтів еластичності попиту по доходу для всіх купованих товарів дорівнює одиниці. Це справедливо для будь-якого числа товарів.
Звідси випливає ще один важливий висновок. Для кожного товару (або товарної групи) з еластичністю попиту по доходу, меншою одиниці, повинен існувати товар (або товарна група) з еластичністю попиту по доходу, більшою одиниці. Це положення і називають зазвичай законом Енгеля. Наведемо ще одне важливе співвідношення: сума коефіцієнтів прямої та перехресної еластичності попиту за ціною і коефіцієнта еластичності попиту по доходу для i-того товару дорівнює нулю. Дійсно, з розділу 3.3 випливає, що при пропорційній зміні всіх цін і доходу, положення бюджетної лінії і, отже, оптимуму споживача (рис. 3.9) не зміниться.
Значить, повний диференціал функції попиту на товар X буде дорівнює нулю:
dX=(dX / dPX) dPX + (dY / dPY) dPY + (dI / dPI) dPI=0.
Якщо ціни і доходи змінилися в (1 + e) раз, то dPX=ePX, dPY=ePY, dPI=ePI. Підставивши ці значення у вираз повного диференціала, скоротивши на t і розділивши всі члени на X, отримаємо:
(dX / dPX) - (PX / X) + (dX / dPY) - (PY / X) + (dX / dI) - (I / X)=0
або, в коефіцієнтах еластичності:
eX + eX, Y + eX, I=0 (4.25)
4.7 Рівняння Слуцького в коефіцієнтах еластичності
Повернемося до рівняння Слуцького (3.17), за допомогою якого ми досліджували вплив ціни товару X на обсяг попиту на цей товар. Тепер ми можемо уявити це рівняння в коефіцієнтах еластичності. Помноживши всі члени рівняння (3.17) на PX / X, отримаємо:
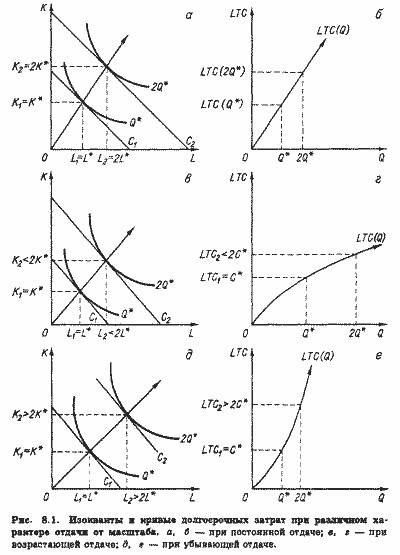
Ліва частина (4.26) представляє не що інше, як коефіцієнт еластичності попиту на товар X - eX.
Перший доданок правої частини можна представити як kXeI, де kX=XPX / I - частка витрат на товар X у загальних витратах покупця I, а eI - коефіцієнт еластичності попиту на товар X за доходом.
Другий доданок правої частини характеризує еластичність попиту на товар X при незмінному реальному доході, позначимо її коефіцієнт -.
Таким чином, ми можемо записати рівняння Слуцького (3.17) в коефіцієнтах еластичності:
eX=-kXeI + (4.27)
Рівняння (4.27) показує, що коефіцієнт еластичності попиту може бути розкладений на два компоненти, що характеризують ефекти доходу і заміни, і відносна величина першого з них залежить від частки витрат на товар X у загальних витратах споживача (kX) - З (4.27) також видно, що для невзаємозамінних товарів (=0) еластичність попиту за ціною пропорційна еластичності попиту по доходу (фактор пропорційності - kX).
Інформація, релевантна "4.4 Еластичність попиту по доходу "
- Ключові терміни
еластичний попит Нееластичний попит Абсолютно нееластичний попит Попит одиничної еластичності Помилка перенесення властивостей частини на ціле Перехресна еластичність попиту за ціною Взаємозамінні і взаємодоповнюючі товари Еластичність попиту по доходу Нормальні і нижчі товари Предмети розкоші і предмети першої необхідності Еластичність пропозиції за ціною Короткострокові - Терміни і поняття
еластичність попиту Коефіцієнт цінової еластичності попиту Перехресна еластичність попиту Еластичність попиту по доходу Гранична корисність Закон спадної граничної корисності Крива байдужості Карта байдужості Гранична норма заміщення Бюджетна лінія Крива - Тема 14. ЕЛАСТИЧНІСТЬ ПОПИТУ І ПРОПОЗИЦІЇ
еластичності. Попит і пропозиція залежать від зміни ціни, однак ступінь залежності окремих товарів різна. Дана особливість товарів враховується допомогою розрахунку еластичності. Еластичність - швидкість реакції попиту або пропозиції на зміну ціни. Якщо її виразити у вигляді процентних змін, то можна розрахувати коефіцієнт еластичності: {foto32} де Еdp-коефіцієнти - Терміни і поняття
еластичний, нееластичний попит, одинична еластичність) Коефіцієнт еластичності попиту за ціною Пропозиція Закон зміни пропозиції Крива пропозиції Коефіцієнт еластичності пропозиції Еластичність пропозиції (одинична еластичність, еластичне , нееластичне пропозицію) Рівновага на ринку Ціна Рівноважна ціна «Ціна статі» і «ціна стелі» Ціна попиту і ціна - Терміни і поняття
еластичний, нееластичний попит, одинична еластичність) Коефіцієнт еластичності попиту за ціною Пропозиція Закон зміни пропозиції Крива пропозиції Коефіцієнт еластичності пропозиції Еластичність пропозиції (одинична еластичність, еластичне, нееластичне пропозицію) Рівновага на ринку Ціна Рівноважна ціна «Ціна статі» і «ціна стелі» Ціна попиту і - Еластичність попиту
еластичності попиту. Поняття еластичності попиту розкриває процес адаптації ринку до змін в основних факторах (ціні даного товару, ціною інших товарів, доходів споживачів і т.д.), що визначають попит . Розглянемо спочатку коефіцієнт еластичності попиту за ціною - показник чутливості обсягу попиту до зміни його ціни. Він визначається як відношення процентної зміни обсягу - Еластичність попиту по доходу
еластичності попиту може бути вибрана не тільки ціна, але і інші економічні змінні. Еластичність попиту по доходу вимірюється як відношення зміни попиту на товар до зміни доходів споживачів. Вимірявши еластичність по доходу, можна визначити, чи відноситься даний товар до категорії нормальних (коли зростання доходів призводить до зростання попиту) або нижчих (коли реакція зворотна). Основна - 1.3.4. Еластичність попиту та пропозиції
еластичність попиту - ступінь зміни попиту у відповідь на 1% зміни ціни . Визначення коефіцієнта цінової еластичності попиту:, де Ed - коефіцієнт цінової еластичності,? Qd (%) - процентна зміна обсягу попиту,? P (%) - процентна зміна ціни. або або, де Q1 - первинний об'єм попиту, Q2 - змінений - Монополія і еластичність попиту
еластичності попиту Ер, а також дані, що характеризують граничні витрати фірми МС, керівництво фірми може розрахувати ціну продукції Р за формулою: {foto48}, (12.1) Чим вище еластичність попиту, тим більше наближені умови діяльності монополіста до умов вільної конкуренції, і навпаки, при нееластичним попиті у монополіста створюється більше можливостей «роздувати» ціни і - Деякі товари, такі як поїздки на автобусі, відносяться до нижчих това-рам: збільшення доходу споживачів веде
еластичністю по доходу. Еластичність за доходом різних нормальних товарів істотно розрізняються ється. Товари першої необхідності, такі як одяг і продукти харчування, характе- ризуются низькою еластичністю по доходу, так як споживачі, незалежно від розмірів доходів, змушені купувати хоча б деякі з них. Предмети рос-коші, такі як ікра та хутра, характеризуються великою - Резюме
еластичність спро-са, вимірює чутливість обсягу попиту на товарка зміни ціни даного товару Вона определяетсякак відношення процентної зміни обсягу спро-са до процентної зміни ціни. 2. Значення еластичності попиту за ціною вздовж лінійної (прямолінійною) кривої попиту змінюється. Онависока при високій ціні і низька при низькій ціні 3. Якщо еластичність попиту перевищує 1, то - Основні терміни і поняття
еластичність, еластичність по доходу, пропозиція, закон пропозиції, еластичність пропозиції, ринкова рівновага, ціна ринкової рівноваги, рента (надлишок) споживача, порушення рівноваги, «нормальна» ринкова - 9.2.5.3. ЕЛАСТИЧНІСТЬ ПРОПОЗИЦІЇ У короткий період
еластичності пропозиції. Еластичність пропозиції за ціною характеризує відносну зміну пропозиції i-го товару при зміні його ціни. Коефіцієнтом прямої еластичності пропозиції за ціною називають відношення відносної зміни обсягу пропозиції у відсотках до відносного зміни ціни. Для характеристики перехресної еластичності пропозиції вводиться додатковий - Питання для самоперевірки
еластичність? Що відображає еластичність стосовно попиту і пропозиції? 2. Фірма вирішила підвищити ціну на свою продукцію. Що станеться з її виручкою, якщо попит еластичний (нееластичний)? 3. Розрахуйте показники цінової еластичності попиту на продукцію фірми, виходячи досліджують даних про обсяги продажів при різних цінах: {foto30} Скільки продукції буде продавати фірма? Наскільки