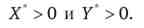
| Головна |
| « Попередня | ЗМІСТ | Наступна » |
|---|
Оптимальну поведінку споживача означає, що він прагне витратити свої гроші найбільш ефективно, т. Е. Так, щоб корисність вибраного набору виявилася максимальною. Однак це не означає, що споживач завжди буде купувати обидва товари (або всі можливі продукти товарного світу). Ми можемо говорити про два види оптимуму.
внутрішній оптимум спостерігається тоді, коли споживач купує позитивні обсяги всіх товарів (обох продуктів в світі двох товарів). Якщо мова йде про двох товарах, то внутрішній оптимум знаходиться всередині області бюджетного безлічі, так що
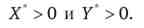
кутовий (крайової) оптимум (Розташований на одній з координатних осей) спостерігається тоді, коли при наявності двох товарів один з них купується споживачем, а інший - ні. Це така рівновага, коли
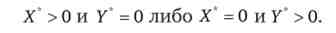
У ситуації з N товарами кутовий оптимум має місце, коли не купується один або кілька товарів.
Аналіз умов кутового і внутрішнього оптимумів вимагає дослідження умов Куна - Таккера першого порядку.
Якщо в набір споживача входить N товарів, то для кожного товару X повинні виконуватися умови Куна - Таккера:
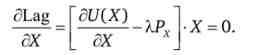
Виконання умов Куна - Таккера можливо в двох варіантах.
т. е. якщо ^ Х
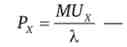
ціна товару в точці оптимуму дорівнює грошовій оцінці граничної корисності останньої купується одиниці (граничної цінності товару), то X > 0 і товар X купується споживачем.
2. Якщо ж ° UW) < yj> т. е. якщо
ДХ х'
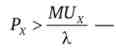
ціна товару є більшою за його граничної корисності для споживача, то X = 0 і даний товар не буде купуватися, оскільки споживач не готовий віддати необхідну суму за одиницю товару. Іншими словами, товар не варто в очах споживача запитуваних грошей. Таким чином, екві- маржинальний принцип визначає, чи буде товар взагалі купуватися раціональним споживачем в стані оптимуму.
Крім того, умови Куна - Таккера визначають необхідність виконання бюджетного обмеження споживача як рівності.
Згідно з умовами Куна - Таккера
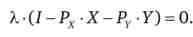
Так як X > 0, оскільки споживач купує якийсь товар, гранична корисність доходу для нього не може бути рівною нулю. Отже, бюджетне обмеження має виконуватися як рівність: I-Px-X-Py Y = 0, споживач в оптимумі повністю витрачає свій дохід.
У зв'язку з цим для внутрішнього оптимуму виконується еквімаржіналь- ний принцип і обидва товари купуються: X " > 0; У ' > 0.
u (MUY Л
У разі кутового оптимуму для одного з товарів - > X покупка
цього товару не варто запитуваних за нього грошей (його ціни). Тому купується тільки один товар: X * > 0; У * = 0.
Тепер ми розуміємо, чому закон попиту повинен виконуватися. За кожну одиницю товару споживач готовий віддати суму: Pt = -L = MV:, рав-
X
ву граничної цінності обсягу товару, що купується. З його збільшенням гранична корисність товару зменшується, і так як у нас немає підстави припускати швидких змін граничної корисності грошей, то ціна, яку споживач готовий віддати за більшу кількість продукту, також знижується, оскільки падає гранична цінність додаткової покупки. Так виходить негативна залежність між ціною товару і обсягом покупки.
Завдання, що ілюструє проблему
Нехай переваги споживача описуються функцією корисності Кобба - Дугласа: U = Х? Y. Відомо, що ціна одиниці товару Х = 2 руб., А ціна одиниці товару Y = 4 руб. Споживач має можливість витратити на придбання товарів 100 руб. Визначте, яка кількість кожного товару купить раціональний споживач. Який при цьому буде досягнутий рівень корисності? Яка буде гранична корисність рубля для нашого споживача?
Рішення
Для знаходження оптимального товарного набору споживача використовуємо метод Лагранжа. Завдання максимізації цільової функції (в даному випадку функції корисності) при наявності обмеження (в даному випадку бюджетного обмеження: 100 = 2Х + 4У) замінюється завданням знаходження максимуму штучно створюваної функції Лагранжа. Побудуємо функцію Лагранжа для нашої задачі: Lag = Х Y + X- (100 - 2х 4У).
Випишемо наступні умови першого порядку для знаходження максимуму:
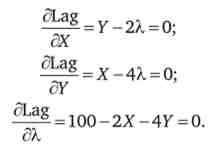
Зауважимо, що останній вираз всього-на-всього повторює бюджетне обмеження. Переносячи складові з X в праві частини першого і другого рівнянь, ми маємо: Y = 2Х ІХ = 4х. Звідки отримуємо, що споживання товарів в точці оптимуму пов'язано співвідношенням: X = 2Y. Підставляємо його в бюджетне обмеження: 100 = 47+ 4Y = 8Yі знаходимо рівноважні значення: Y '= 12,5; Х = 25. Таким чином, набір (X = 25; У '= 12,5) є оптимальним вибором споживача.
Така кількість товарів X і Y купить раціональний споживач при даних цінах і даному рівні доходу.
Максимальний рівень корисності складе шах [/ = Х - Y = 312,5 утиль.
Ми можемо знайти також значення множника Лагранжа (X) в точці оптимуму
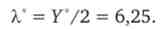
Це значення говорить про те, що кожен додатковий рубль при оптимальному використанні принесе споживачу додатково 6,25 од. корисності.
Завдання, що ілюструє теорію
Уподобання індивіда щодо отримання освіти (X) і всіх інших товарів (У) мають стандартний вигляд, і його вихідний вибір включає кілька обох товарів. Прагнучи схилити споживача до вибору більшого кількостях, уряд розглядає питання про введення однієї з двох схем: а) грошової субсидії на одиницю споживання освітніх послуг; б) ваучера (фіксованої суми грошей, що підлягає витрачанню лише на освіту).
Рішення
1-2. Розглянемо бюджетні лінії для субсидії ваучера (схема «б», рис. 1).
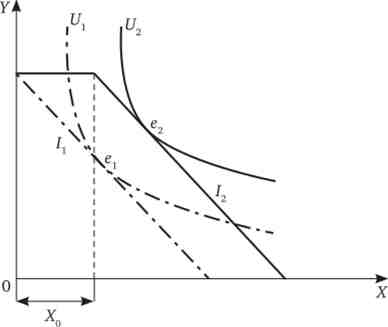
Мал. 1
Держава дає громадянам субсидію у вигляді ваучера на певну суму грошей на освіту (товар X). Оскільки цей ваучер неможливо ні продати, ні використовувати інакше, то будемо вважати цю субсидію натуральної в розмірі Х0 (Див. Рис. 1). бюджетне обмеження It = Р.: ? X + Ру- Y, яке було до введення субсидії, зміниться бюджетним обмеженням /2 = Р: ? (X - Х0) +Py-Y. На графіку крива також зрушиться від до /2, а значить, кращий набір продуктів ех > е2 виявиться на більш високій кривій байдужості (t /2), Т. Е. Більш високому рівні корисності.
Припустимо тепер, що уряд виділяє субсидії, які знижують плату за навчання на s відсотків (схема «а»). Тому громадянин в даному випадку повинен платити (1 -.?) ? Рх за кожну одиницю навчання: / = (1 - s) ? Рх ? X + PY ? Y. Виділення субсидії змінило бюджетне обмеження (бюджетне обмеження до введення субсидії В ,, а після В2).
Тепер найкращим набором продуктів громадянина є точка е2. Вона належить кривій байдужості U2, яка лежить вище Ur
3. Можливий також варіант, що уряд виділить громадянам акордні субсидії (схема «в»). Це еквівалентно збільшенню бюджету громадянина, т. Е. Бюджетне обмеження зросте до рівня В3: 1 + Т = Рх ? X + Ру ? Y. У цьому випадку найкращим набором продуктів громадянина є точка е3 (Рис. 2). Вона належить кривій байдужості U2, яка лежить вище U ,. але Х3 < Х2 з огляду на те, що ставлення цін товарів X і У різний у другому і третьому випадках. Більш дешеву освіту сприяє збільшенню кількості товарах в споживчому наборі.
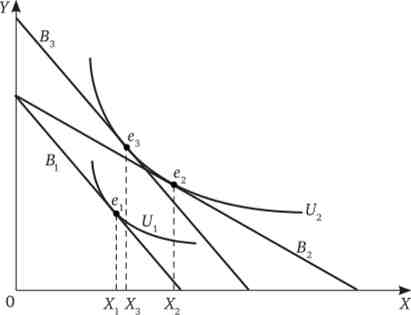
Мал. 2
Якщо припустити, що всі три схеми субсидування обійдуться в одну і ту ж суму, то уряд вибере схему «а» (грошова субсидія на одиницю споживання), так як в разі натуральної субсидії знайдеться частина людей, яким така кількість освіти Ха просто не потрібно, а це втрати для суспільства. А схема «в» (акордна субсидія) збільшить загальну корисність для споживача, але в меншій мірі, ніж схема «а» за рахунок утворення X (Див. Рис. 2).