модель Марковіца

Припустимо, що індивід здійснює вибір між двома активами - безризиковим і ризиковим способом вкладення грошей. Кожен вид активу володіє двома характеристиками - прибутковістю і ризикованістю. Як прибутковості активу можна розглянути очікуваний приріст його вартості через рік. Якщо Wj - вартість активу в поточному році, то W₂ - очікувана стои-

W.- W

мість активу через рік. Тоді: г, = - ^ 00% "надає прибутковості h-o

активу. Приймемо прибутковість безризикового активу за г " а прибутковість ринку капіталу в цілому (всі цінні папери, що котируються на біржі, або всі активи в економіці) - за р

Вкладення в цінні папери інших компаній називаються ризиковими активами, так як надходження по ним відрізняються більшим чи меншим ступенем нестабільності та невизначеності. Для зниження ймовірності невдачі в разі ризикованих активів розподіл коштів відбувається у вигляді портфеля - набору ризикованих активів різного роду, оптимізація якого становить головне завдання фірми на фінансовому ринку. Розглянемо докладніше, яким чином здійснюється вибір фірмою оптимального портфеля ризикованих активів - цінних паперів.

Механізм подібного вибору було запропоновано вперше Г.Марковіцем.

Історична довідка

Гаррі Макс Марковіц (Нар. 1927 г.), американський економіст. Закінчив Чиказький університет. Лауреат Нобелівської премії з економіки 1990 р за роботи з теорії фінансової економіки. Є основоположником сучасної портфельної теорії, їм було запропоновано новий підхід до дослідження ефектів ризику розподілу інвестицій, кореляції і диверсифікації очікуваних інвестиційних доходів. Працював в дослідницькому відділі корпорації RAND, в Каліфорнійському і Пенсільванському університетах. У 1974-1983 рр. займався економічними розробками в Науково-дослідному центрі ім. Т. Уотсона компанії IBM. В наступні роки був професором Нью-Йоркського міського університету. Роботи Г. Марковіца присвячені дослідженням ринку цінних паперів, інвестицій, оптимізації, лінійного програмування.

Ризикованість портфеля вкладень (і окремого ризикового активу) може бути оцінена за допомогою різного роду показників.

Ризик виникає внаслідок того, що фактичне значення прибутковості не збігається з очікуваною. Прибутковість ризикового активу і портфеля ризикових активів є величиною випадковою, схильною до розкиду. Чим ширше розкид значень випадкової величини, тим вище ймовірність відхилення фактичної величини доходу від очікуваної. Тому в якості міри ризику приймають показники варіабельності доходу, до яких відносяться:

? дисперсія: D = a² = '^ P_i(x_l-xf,

де р - ймовірність г-го результату (прибутковості в i-й ситуації); Х.- прибутковість в i-й ситуації; х - середня прибутковість величини за період;

? стандартне відхилення: о = JD;

Я коефіцієнт варіації: V = -.

х

Значення даних коефіцієнтів показують відносний ризик в залежності від масштабу вкладень. Високі значення показників вказують на низьку якість доходів, означають підвищений ризик і відображають варіацію між дійсними доходами і змінами доходів.

Вибираючи пропорції вкладення своїх коштів в ризиковий і безризиковий активи, індивід прагне максимізувати власну функцію корисності, компонентами якої є прибутковість і ризикованість: U = U (W, а). Так як більшість людей не схильні до ризику, то ми можемо ввести такі передумови: прибутковість - це благо для індивіда:

dU (W, a) _n - dU {W, o). " _й

• ---> 0, аріек - антиблаго: ---<0. Тоді криві байдужості
• 8W SW

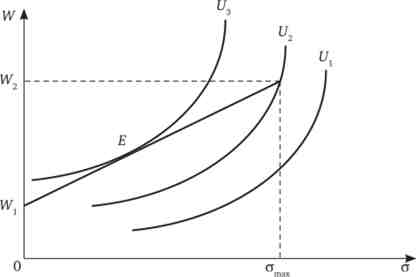
матимуть позитивний нахил (рис. 20.1). Як і у випадку традиційної теорії поведінки споживача, всі портфелі (пропорції вкладення коштів), що знаходяться на одній і тій же кривій байдужості, рівноцінні для індивіда. Будь-портфель, розташований на кривій байдужості, яка проходить вище і лівіше, оцінюється як більш привабливий, ніж вкладення на кривій байдужості нижче і правіше.

Якщо всі засоби індивіда вкладені в безризиковий актив, то приймемо ризик за нульову точку: ст = 0, а прибутковість - за мінімальну величину W. Якщо всі засоби індивіда вкладені тільки в ризикові активи, то загальний ризик портфеля максимальний: ст_тах, хоча максимальна і очікувана прибутковість W. Всі інші можливі пропорції розподілу коштів знаходяться між цими двома крайніми позиціями в якості їх лінійних комбінацій. Тому W₂ = W_l+ ba або у відсотках: r₍ = r_{ + р, - (г - r_f)

(Де р, = - - коефіцієнт бета, який показує відносну ріспост

ванность i-ro активу (i-й цінного паперу) в порівнянні з ринком капіталу в цілому). Ця лінія має назву «Лінія ринку капіталу». Вона служить бюджетним обмеженням для індивіда.

Мал. 20.1. модель Марковіца

Лінію бюджетного обмеження можна інтерпретувати в такий спосіб.

Якщо г, - дохід на безризиковий актив (наприклад, державні короткострокові зобов'язання, отримання доходу за якими практично завжди гарантовано урядом для будь-якого періоду часу і будь-якого економічного агента), то плата за додатковий ризик може бути виражена у вигляді додаткового доходу для ризикових активів:

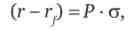
де Р - ціна одиниці ризику.

Рівновага на ринку ризикових активів буде в точці дотику кривої байдужості і лінії ціни ризику - лінії бюджетного обмеження. Це буде точка оптимального співвідношення прибутковості активу і його ризику - точка Е.

Таким чином, оптимальний вибір фірми є розподіл грошових коштів між різними активами до тих пір, поки не буде виконуватися наступне співвідношення:

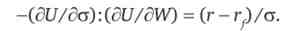
Вибір ризикового портфеля і диверсифікація

Дуже часто індивід здійснює вибір не тільки між безризиковим і ризиковим активом, але і між різними видами ризикових активів, складаючи оптимальний для себе портфель

вкладень.

Оскільки в портфель ризикових активів входять цінні папери та інші вкладення різного роду, можливе виникнення їх взаємного впливу.

Оцінка ризику взаємодії двох випадкових величин х і у проводиться за методом стохастичної залежності. нехай q - ймовірність того, що змінна у прийме значення ^ тоді, коли змінна х прийме значення х .. Характер залежності двох випадкових змінних відбивається в матриці ймовірностей (табл. 20.1).

У портфельному аналізі використовують дві кількісні заходи взаємозалежності двох випадкових змінних.

- ковариацию:

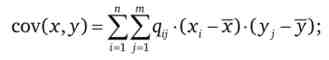
- коефіцієнт кореляції:

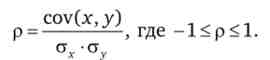
Коваріація показує, наскільки дві випадкові змінні, такі, як прибутковості двох цінних паперів, залежать один від одного. Якщо ковариация більше нуля, це означає, що прибутковості (або ціни) двох цінних паперів мають тенденцію змінюватися в одному напрямку, так що, наприклад, зростання прибутковості або ціни однією з цінних паперів, швидше за все, спричинить за собою збільшення прибутковості або ціни іншого . Негативна коваріація демонструє протилежну залежність між показниками двох цінних паперів. Зростання ціни одного цінного паперу буде, ймовірно, супроводжуватиметься падінням ціни або прибутковості інший. Якщо значення коваріації наближається до нуля або дорівнює йому, то зв'язок між параметрами цінних паперів відсутня або дуже слабка.

Коефіцієнт кореляції використовується для полегшення порівняння динаміки випадкових змінних з іншими параметрами, оскільки унормовує ковариацию. Якщо р = -1, між змінними спостерігається повна негативна кореляція. Якщо р = 1, спостерігається повна позитивна кореляція. При р = 0 зв'язок між змінними відсутній.

Завдання, що ілюструє концепцію

Випадкова змінна х (наприклад, ціна акцій компанії А) з ймовірністю 0,3 може прийняти значення 50, з імовірністю 0,2 - значення 100, з імовірністю 0,5 - значення 130. Випадкова величинау (наприклад, ціна акцій компанії В) може прийняти з ймовірністю 0,6 значення 150, з імовірністю 0,4 - 275. Імовірність спільного появи велічінх иу представлені в таблиці:

Знайдіть показники коваріації і кореляції для портфеля вкладень. Рішення

Обчислимо середні величини для кожного цінного паперу

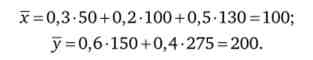
Знайдемо показники середнього квадратичного відхилення 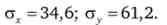Розрахуємо значення коваріації

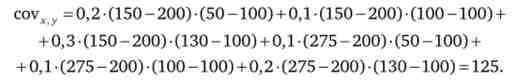
Знайдемо коефіцієнт кореляції

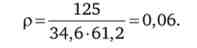
Дане значення показує, що ціни наявних активів дуже слабо корре- ліровать між собою (т. Е. Взаємопов'язані). динаміка змінної х практично ніяк не відбивається на поведінці змінної у.

Як же скласти оптимальний портфель з кількох ризикових активів?

Припустимо, що індивід хоче розподілити свої кошти між двома видами цінних паперів - акцій компанії А і акцій компанії В. Відомі показники ризику і прибутковості для цих цінних паперів: відповідно (а_д, г_л) І (ст_в, г_в). Нехай а - частка акцій компанії А в портфелі індивіда (інвестора). Тоді середня прибутковість портфеля буде дорівнює: г = аг_л + (1 - а) 7_1г Це і є очікувана прибутковість портфеля вкладень.

Ризик портфеля знаходиться за формулою дисперсії суми двох випадкових змінних:

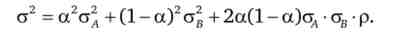
Якщо очікувана прибутковість інвестиційного портфеля являє собою середньозважену з середніх доходностей цінних паперів, де в якості ваг використовуються частки активів у вкладенні, то ризик комплексних вкладень є більш складним за своєю природою. Залежно від кореляції прибутковості активів, т. Е. В залежності від характеру взаємозв'язку динаміки цінних паперів, ризик портфеля може як зменшуватися, так і збільшуватися в порівнянні з сумою ризиків окремих вкладень самих по собі.

ШПАРГАЛКА

Дисперсія суми двох випадкових величин

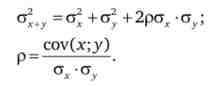
Дисперсія суми твори двох випадкових величин на константи 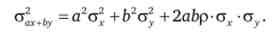Розглянемо окремий випадок.

нехай г^еЛ = Г '= г^е і а^зл = про_в = про^е, т. е. доходності і ризики цінних паперів однакові. Припустимо, що індивід вкладає половину своїх коштів в акції компанії Л і половину-в акції компанії В: а = 1/2. Прибутковість портфеля буде дорівнює середньої прибутковості будь-який з цінних паперів.

А ризик портфеля складе

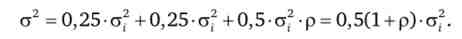
Якщо р = 0, т. Е. Паперу не пов'язані і не корелюють один з одним, то:

про² = 0,5о². В цьому випадку дисперсія портфеля виявляється рівною тільки половині дисперсії кожного з вкладень окремо.

Якщо р = -1, то а² = 0. У даній ситуації у портфеля активів ризик відсутній, ми отримуємо безризиковий портфель вкладень.

Якщо р = 1, то а² = а². Тепер ризик портфеля дорівнює ризику однієї з цінних паперів, і він є максимальним для даного випадку.

Таким чином, правильна диверсифікація портфеля зменшує сукупний ризик. Дисперсія портфеля вкладень менше (або в крайньому разі, не більше) середньозваженої суми дисперсій входять до нього активів.

Знаючи, як пов'язані між собою дисперсія портфеля вкладень і частка, що припадає на один цінний папір, можна знайти оптимальну а, при якій ризик портфеля мінімальний. Для цього обчислимо умова пер- dcr²(A)

вого порядку: - = 0. Звідки отримуємо

da

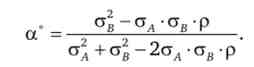
Знайдемо оптимальні частки акцій при різних значеннях коефіцієнта кореляції:

а) якщо р = -1, то а "= ---; (1-а) = ---;

а² а²

б) якщо р = 0, то а '= , ^в (1 - а) "= , ^л ;

а²+а² а²+а²

в) якщо р = +1, то а * = ---; (1-а) = ---.

^СТА ~ ° В ^аА ~

У кожному з цих випадків при дотриманні оптимальних часткою індивід отримує безризиковий портфель: а² = 0.

Звернемо увагу на останній випадок. Коли прибутковості цінних паперів позитивно корелюють між собою, то

• якщо ст_в > про_д, (1 - а) <0;
• якщо ст_в < О так < 0.

Це означає, що в оптимальному портфелі частка однієї з акцій повинна бути менше нуля і індивід повинен продавати цінні папери «без покриття», не маючи їх в наявності. Дана ситуація носить назву «короткі продажі».

Однак не всім індивідам потрібен мінімальний ризик портфеля. Деякі інвестори готові нести більш високий ризик, якщо їм запропонують портфель з більш високою очікуваною прибутковістю.

Висловимо з рівняння: ст²(А) = а²ст²-К1-о0ств + 2а (1-а) а_л ст_в р значення частки а як функції від ризиків цінних паперів та портфеля в цілому: а = а (а_л, про_в, а²). Підставами це значення в рівняння середньої прибутковості портфеля: г = аг_А + (1 - а) г_в. В результаті ми отримаємо функціональну залежність між прибутковістю і ризиком портфеля в залежності від коефіцієнта кореляції: г^е = / (Про², р).

Графічно ця залежність при різних р представлена на рис. 20.2.

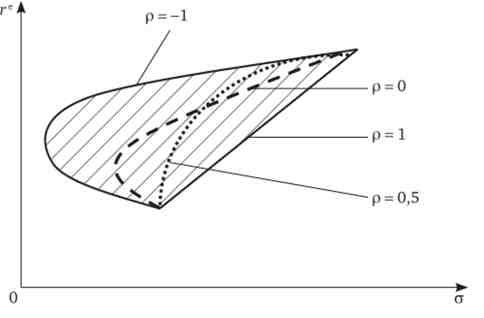
Мал. 20.2. Ефективне безліч портфелів

Так як коефіцієнт кореляції не може бути більше 1 і менше (-1), лінія залежності між ризиком і прибутковістю портфеля вкладень окреслює ефективне безліч можливих портфелів для інвестування. Ефективне безліч володіє двома характеристиками. Будь-портфель з цього безлічі забезпечує: 1) максимальну очікувану прибутковість для деякого рівня ризику; 2) мінімальний ризик для деякого значення очікуваної прибутковості. Ефективне безліч представлено заштрихованої областю на рис. 20.2.

Портфелі, розташовані за межами ефективної безлічі, не є ефективними і ніколи не будуть обрані інвестором.

Кордон ефективної безлічі показує лінію бюджетного обмеження для індивіда, що вибирає оптимальний портфель вкладень.

Уподобання індивіда щодо ризику і прибутковості і тут можуть бути представлені у вигляді функції корисності. Її прикладом може служити функція Рубінштейна: U = - г^е - про² (де ^VF - індивідуальні переваги інвестора щодо дохідності та ризику). Як параметр Т можна використовувати індекс Пратта - Ерроу, розглянутий в гол. 10.

Висловивши значення прибутковості портфеля через змінну ризику (дисперсії портфеля), отримуємо криві байдужості з позитивним накло-

_е U а² ном: г = - + -.

??

Тепер за допомогою звичайних методів оптимізації можна знайти максимальну корисність при обмеженні, описуваному кордоном ефективної безлічі. Оскільки для індивіда, не схильну до ризику, криві байдужості випуклі і мають позитивний нахил, а межа ефективної безлічі увігнута, це рішення буде єдиним. На рис. 20.3 показано рівновагу інвестора при виборі тільки ризикових активів і наявності безризиковою альтернативи.

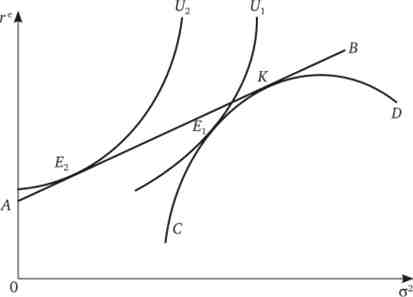
Мал. 20.3. Оптимальний вибір інвестора портфеля ризикових активів

Якщо індивіду пропонуються тільки ризикові активи, то лінія CD характеризує кордон ефективної безлічі портфелів. Оптимум інвестора знаходиться в точці? ,, точці дотику лінії CD і кривої байдужості U_v При включенні одного безризикового активу індивід буде орієнтуватися на лінію АВ, показує тепер його бюджетне обмеження (як в моделі Марковіца, проаналізованої вище). Так як вибір здійснюється на основі однакового набору ризикових вкладень, до яких тільки додається один безризиковий актив, лінія АВ повинна стосуватися лінії CD. На рис. 20.3 ця умова виконується в точці К. Однак вона ніколи не буде обрана, оскільки характеризує портфель з більш високим ризиком, ніж набір в точці Е_у Це підтверджує і той факт, що точка До розташована на менш бажаною кривої байдужості.

Чи буде обраний портфель з безризиковими активом, якщо є портфелі тільки з ризиковими активами? Так, для індивіда, не схильну до ризику, крива байдужості, відповідна вибору портфеля з безризиковими активом, розташована лівіше і вище, ніж вибір виключно ризикового набору. Оптимум в даному випадку буде перебувати в точці Е_у відповідної кривої байдужості U₂. А так як U₂U_X, портфель Е₂ виявиться для інвестора краще портфеля Е_у

Припустимо, що в розпорядженні інвестора виявляються N ризикових активів. Нехай інвестор дотримується принципу «наївною» диверсифікації, розподіляючи свої кошти рівномірно

Оптимізація портфеля з N цінних паперів

між усіма видами цінних паперів, так що а = -.

Ризик складеного таким чином портфеля буде дорівнює

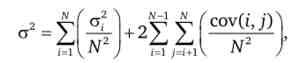
де вираз: Х | "~ 2" | ^показикість середню варіацію цінних паперів, вхо- ^{1 = 1} ^ ' ^{N_1 N} fcovfi i) ^

дящих в портфель, а вираз 2 ^ ^ характеризує середню

i = i; = i + iV J

ковариацию активів, що входять в портфель.

При збільшенні числа вкладень (при зростанні N) ризик портфеля скорочується. Однак зовсім безризиковий портфель недосяжний. Межею сукупної ризикованості портфеля в бік зниження буде не нуль, а величина середньої коваріації активів (сот). Вона показує недівер- сіфіціруемий ризик інвестицій, який пов'язаний з непередбаченими подіями в національній та світовій економіці. Та частина ризику, яка може бути знижена до нуля при диверсифікації портфеля, називається відповідно діверсіфіціруемий ризиком. Такий ризик є специфічним для конкретних галузей і конкретних фірм.

Таким чином, залежність ризикованості портфеля від числа видів вкладень має вигляд монотонно спадної лінії, обмеженою знизу значенням (сот) (рис. 20.4).

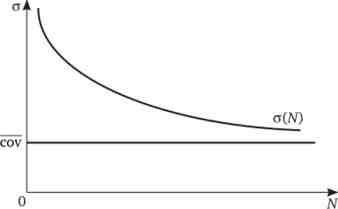
Мал. 20.4. Діверсіфіціруемий і недіверсіфіціруемий ризик портфеля

Питання для роздумів

Згідно з дослідженнями встановлено два види ризикованості вкладень:

• 8 63
• 1958-1967 рр., Нью-Йоркська фондова біржа: ст = 11,91 + -;

N

• 11 27
• 1980-і рр., Швейцарський фондовий ринок: ст = 16,25+ ' .

На якому фінансовому ринку вище в середньому: 1) діверсіфіціруемий і 2) неді- версіфіціруемий ризик? З чим це може бути пов'язано?

коефіцієнт бета

Ризик вкладень при взаємному впливі активів друг на друга вимірюється також за допомогою коефіцієнта бета. Він розраховується як

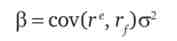
або

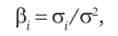
де г^е - прибутковість портфеля ризикованих активів; м-прибутковість безризикового активу; а., а - стандартне відхилення прибутковості відповідно даного цінного паперу і ринку в цілому.

Коефіцієнт бета характеризує систематичний ризик цінних паперів, він вимірює ризикованість даного активу в порівнянні з ризикованістю ринку цінних паперів в цілому. Для безризикового активу (3 = 0.

Коефіцієнт бета показує стан економічної кон'юнктури в цілому на ринку, він представляє собою тангенс кута нахилу виявленої лінійної залежності між загальноринковими прибутками по всіх акціях на біржі в цілому і прибутками по окремих акціях. При подібному зміні ринкових цін і цін на конкретні цінні папери р = 1, зміна загальноринковою ціни на 1% тягне за собою зміну на 1% ціни цих паперів. якщо р < 1, то це означає слабку залежність даних цінних паперів від ринку в цілому, якщо Р > 1 - сильну залежність.

Ці залежності відображені в квадраті I (рис. 20.5).

Якщо залежність руху ринку і курсу даних цінних паперів протилежна, то вона відбивається в квадраті III. Якщо на ринку відбувається збільшення середніх курсів при одночасному зменшенні курсу даних акцій, то це відіб'ється в квадраті II. При виникненні на ринку ситуації, коли середні курси падають, а конкретний курс починає рости, цей процес відбивається в квадраті IV. Це може характеризувати переломний момент у розвитку фондового ринку.

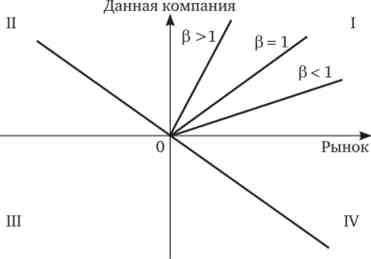
Мал. 20.5. коефіцієнт бета

Акції з коефіцієнтом бета більше одиниці мають більшу мінливістю, ніж ринок в цілому. Тому вони носять назву агресивних акцій. Акції з коефіцієнтом бета менше одиниці характеризуються меншою волатильністю, ніж ринок в цілому. Тому вони називаються оборонними акціями.

Середні значення коефіцієнта бета для деяких галузей промисловості представлені в табл. 20.2.

Таблиця 20.2. Середні значення коефіцієнта бета для галузей промисловості

джерело: Шарп У., Александер Г., Бейлі Дж. Інвестиції. М.: ИНФРА-М, 2003. С. 519. Рівновага на ринку ризикових активів можна розрахувати за допомогою коефіцієнта бета наступним чином.

Ціна одиниці ризику дорівнює: Р = (r^c- r_f) / O. Сукупний ризик для г-го активу дорівнює добутку одиниці ризику для цього активу і обсягу ризику: Тоді ціна сукупного ризику дорівнює: Р = Р_;а = p. (r^e- м).

На ринку відбувається вирівнювання ризику для всіх активів, т. Е.

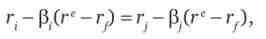
де м - величина доходу на г-й актив; г^е - прибутковість ринку; г_{ - прибутковість безризикового активу.

Таке вирівнювання відбувається і для безризикового активу. Тому 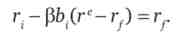тоді

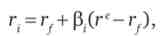
де р. (г^з-м) - премія за ризик.

Отже, прибутковість конкретного цінного паперу (конкретного активу) визначається двома головними параметрами: 1) премією за ризик у порівнянні з безризиковим активом; 2) ступенем волатильності даного активу в порівнянні з ринком в цілому. Цей принцип лежить в основі ціноутворення капітальних активів (capital asset pricing model - САРМ).

1. Проблеми суспільного вибору
   Державні рішення недоліків ринку не завжди призводять до оптимальних результатів. Однією з причин цього є недоліки самого процесу прийняття рішення з боку держави. Рішення про проведення тих чи інших заходів держави приймаються в демократичних державах в органах законодавчої влади шляхом голосування
2. Проблема фінансування виробництва суспільних благ
   Найбільш явною труднощами, пов'язаної із забезпеченням виробництва суспільних благ, є проблема, яка полягає у відмінності переваг різних індивідів, що складають спільноту, для якого і в якому приймається якесь рішення. Якби всі люди були однаковими (характеризувалися б однаковими вподобаннями)
3. Премія за ризик
   Розглянемо докладніше функцію корисності індивіда, не схильну до ризику (рис. 10.3). Візьмемо лотерею з двома наслідками і / 2 ), і нехай р - ймовірність успішного результату. Лінія, що з'єднує точки на кривій корисності, що відповідають цим двом наслідків, показує можливі лінійні комбінації
4. Поведінку самокерованої фірми, вибір оптимальної зайнятості
   Фірма, керована працівниками, які одночасно є і її власниками, носить назву самокерованої фірми. На відміну від фірми, власником якої є один індивідуальний власник, тут є безліч власників. На відміну від акціонерного товариства на самокерованої фірмі власники самі працюють, а не тільки вкладають
5. Попит і пропозиція на ринку капіталу
   Формування попиту на кредитні гроші відбувається тоді, коли в первісній ситуації у споживача або фірми менше поточних грошей (економічний агент отримав менший дохід або більше цінує поточну грошову одиницю), ніж необхідно для рівноважного стану: /, < З *. Отже, індивід і фірма будуть брати
6. Підхід з точки зору часткової рівноваги
   Та ж сама концепція оптимального обсягу виробництва суспільного блага може бути виражена за допомогою інструментарію часткової рівноваги. На рис. 23.4 зображений ринок громадського блага, взятого самого по собі. Крива попиту на дане суспільне благо з боку індивіда А представлена лінією Е л
7. Оцінка ринкової влади фірми
   Монопольна ціна дозволяє оцінити ступінь ринкової влади фірми. Хоча ситуація монополії на увазі наявність на ринку єдиного продавця товару, що означає максимальну ринкову владу на даному ринку, різні ринки можуть допускати різну ступінь монопольної влади. В умовах досконалої конкуренції ринкова
8. Оптимальні сайти: досвід провідних компаній
   Аналіз найбільш вдалих сайтів російських і зарубіжних компаній, що діють на російському ринку, дозволяє виділити кілька Передбачається, що сайт повинен стимулювати позитивний настрій потенційного клієнта. З огляду на, що відвідувачі спочатку здійснюють самих поверхневий, швидкий перегляд релевантний